Пример.. Пример.. Вектор нормали к поверхности. Вторая квадратичная форма поверхности. Пример.. Главные кривизны

⇐ ПредыдущаяСтр 5 из 5

Пример.

Найти угол между координатными линиями u=const и v = const

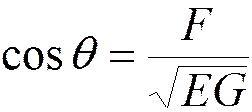
Решение.

Обозначения E = (r₁₀)²,F = r₁₀•r₂₀,G = (r₂₀)²

Поэтому dr dr= r₁du¹ r₂du²= F du¹du²

|dr||dr|=√(dr dr)√(drdr)= √(E G) du¹du²

Пример.

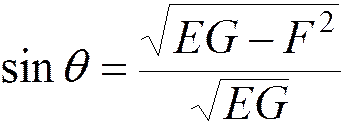
Вектор нормали к поверхности

Пусть M — элементарная поверхность в E³ , r = r(u,v) — ее параметризация.

В каждой точке pÎM существует единственный вектор единичной длины

Этот вектор называется вектором нормали к поверхности M в точке pÎ M.

Базис r_u,r_v, n называется сопровождающим базисом повекхности.

Т.к. |r_u´r_v|² = EG-F² , то

Док-во. |r_u´r_v|=|r_u||r_v|sinq,

|r_u|²=E = (r_u₀)², |r_v|²=G = (r_v₀)², F = r_u₀•r_v₀

Вторая квадратичная форма поверхности

Производная r"(s) при s = 0 пропорциональна вектору n (r' = r_uu' + r_vv').

Соответствующий коэффициент пропорциональности называется относительной кривизной k.

Таким образом,

r" • n = k

Поскольку

r" = r_uu u'² +2r_uv u'v' + r_vv v'² + r_uu" + r_v v',

то

k = L u'² + 2M u' v' + N v'² ,

где

L = r_uu•n, M = r_uv•n, N = r_vv•n.

Т.к. k(t) — билинейная форма и dr = t ds , то

k(t) =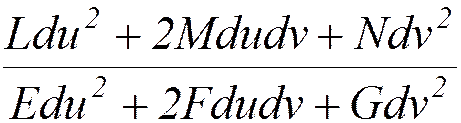

Квадратичная форма II= 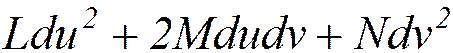называется второй квадратичной формой поверхности M .

Относительная кривизна k(t)=II/I.

Пример.

Показать, что II=- dr•dn.

Главные кривизны

Французский математик Дюпен предложил рассматривать в касательной плоскости кривую, определяемую уравнением

|L x² +2M xy +N y²|=1.

При LN- M² >0 точка поверхности называется эллиптической, индикатриса - эллипс; LN- M²<0 точка поверхности называется гиперболической, индикатриса состоит из двух гипербол, при LN-M²=0 точка поверхности называется параболической, индикатриса состоит из двух параллельных прямых.

В эллиптической точке все кривизны k(t)>0, среди них одна наибольшая k₁ и одна наименьшая k₂ (в направлении главных осей). Если индикатриса является окружностью, то все кривизны равны.

В гиперболической точке в направлении действительной оси одной гиперболы k₁>0, в направлении действительной оси другой гиперболы k₂<0

В параболической точке в направлении параллельных прямых k₁=0, в перпендикулярном направлении |k₂| достигает наибольшего значения.

Числа k₁ и k₂ называются главными кривизнами.

Их произведение K= k₁ k₂ называется полной или гауссовой кривизной.

Их полусумма H= (k₁+k₂)/2 — средней кривизной.

Пример.

Показать, что

⇐ Предыдущая 1 2 3 45