Хелпикс

Главная

Контакты

Случайная статья



ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТИ. Определение гладкой гиперповерхности.. Кривая на гиперповерхности. Касательный вектор гиперповерхности

Стр 1 из 5Следующая ⇒


ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТИ

Оказывается, что условия вида

F(x1,…,xn)=0

в Rn недостаточно для определения некоторой гиперповерхности.

Необходимо привлечь условие регулярности:

должен быть отличен от нуля вектор

.

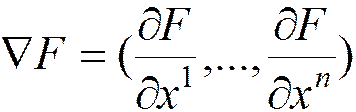Определение гладкой гиперповерхности.

Множество всех точек x=(x1,…,xn) открытого множества UÌRn, удовлетворяющих условию

F(x1,…,xn)=0,

где F - гладкая на U функция, называется гладкой (регулярной) гиперповерхностью в U, если каждой точке xÎU хотя бы одна частная производная

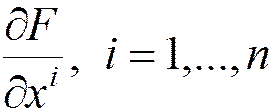
отлично от нуля.

Графиком гладкой функции xn=f(x1,…,xn-1), заданной на открытом множестве VÌRn-1, называется множество всех точек вида

(xn, f(x1,…,xn-1))Î Rn .

График любой гладкой функции является гиперповерхностью, ибо ¶F/xn= − 1 ¹ 0 для любой точки x

(неявная функция - F=f(x1,…,xn-1) − xn = 0).

Кривая на гиперповерхности

Кривая x=x(t) лежит на гиперповерхности

F(x) = 0,

пространства An, если F(x(t)) = 0 для любого tÎ[a,b], т.е. гиперповерхности принадлежит носитель кривой.

Касательный вектор гиперповерхности

Вектор u называется касательным вектором гиперповерхности в ее точке x0, если на гиперповерхности лежит кривая

x : t"x(t),

проходящий через точку x0 при t = t0, что u является касательным вектором этой кривой в точке t = t0, т.е. u = x'(t0)

Пусть Vn - линеал, ассоциированный с An, и Ηx0 - множество всех векторов, касательных к гиперповерхности в ее точке x0  (Ηx0 Ì Vn).


12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.