Теорема.. Гиперплоскость. Элементарные поверхности и их параметризация

Теорема.

Множество Η_x₀, является n-1-мерным подпространством пространства Vⁿ, состоящим из всех векторов, ортогональных ковектору ÑF :

Η_x₀ = { aÎVⁿ | a•ÑF = 0}.

Док-во.

Дифференцируем функцию F(x(t)) = 0

dF(x(t))/dt = x'(t)•ÑF = 0

Гиперплоскость

Гиперплоскость пространства Aⁿ, проходящая через точку x₀ параллельно пространству Η_x₀, называется касательной гиперплоскостью к гиперповерхности (3) в точке x₀ .

Элементарные поверхности и их параметризация

Рассмотрим отображение вида

g: U "Aⁿ, (*)

где U — выпуклое (содержит каждый прямолинейный отрезок, концы которого принадлежат U) открытое подмножество арифметической плоскости R² , Aⁿ — некоторое точечно евклидово пространство.

Когда в Aⁿ выбрано начало отсчета, отображение (*) задается непрерывной вектор-функцией

x = x(u,v), (u,v) Î U, (1)

принимающей значения в ассоциированном линеале Vⁿ.

Числа (u,v) Î U называют координатами точки p = g(u,v) Î Aⁿ

Если в Aⁿ выбран базис e_i, то отображение (1) задается непрерывными числовыми функциями

x¹ = x¹(u,v),…, xⁿ = xⁿ(u,v)

— координатами в базисе e_i вектора x.

Для гладких отображений определены частные производные

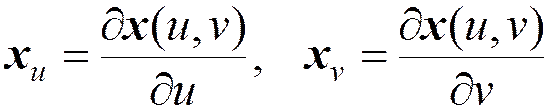
Поверхность называется регулярной, если в каждой точке векторы x_u и x_v линейно независимы.

Отображение (1) x = x(u,v), (u,v)ÎU, называется параметризацией, если оно

1. гладко,

2. регулярно,

3. монеоморфно (инъективно и из сходимости последовательности точек g(u_n,v_n) в Aⁿ следует сходимость последовательности (u_n,v_n) в U)

Подмножество M Ì Aⁿ называется элементарной поверхностью, если существует такая параметризация g: U"Aⁿ, что g(U) = M.

Параметризация поверхности M кривую в U, заданнуюпараметрическими уравнениями

u = u(t), v = v(t), tÎI,

переводит в кривую

x = x(u(t),v(t)), tÎI

пространства A.

Пусть U, U*ÌR². Тогда диффеоморфизм

j: U*"U

осуществляет замену координат.

Диффеоморфизм — биективное отображение, имеющее гладкое обратной отображение.

⇐ Предыдущая 123 4 5 Следующая ⇒