
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Векторным произведением a´b векторов a, b называют вектор дополнительный к их внешнему произведению aÙb
Векторным произведением a´b векторов a, b называют вектор дополнительный к их внешнему произведению aÙb
a´b=( aÙb)^
Касательная плоскость
Пусть M — элементарная поверхность в An с параметризацией
r = r(u,v),
p — точка поверхности M , r0 = r(u0,v0) — ее радиус вектор. В силу регулярности значения
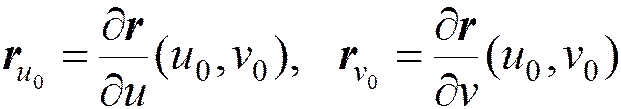
частных производных вектор-функции r0 = r(u0,v0) в точке (u0,v0) линейно независимы, поэтому бивектор ru0 Ù rv0 отличен от нуля.
Векторы ru0 и rv0 определяют двумерную плоскость, проходящую через точку p = g(u0,v0) с направляющим бивектором ru0 Ù rv0
Касательной плоскостью поверхности M в точке p0 называют плоскость, векторное параметрической уравнение которой имеет вид
r = r0 + aru0 + brv0,
где a, b — параметры. Соответствующее подпространство ассоциированного линеала V (состоящего из векторов aru0 + brv0) обозначается символом Kp0M и называется касательным подпространством.
Векторы подпространства Kp0M обозначаются dr, а их координаты в базисе (ru0, rv0) символами du и dv.
Первая квадратичная форма
Пространство An считаем евклидовым. Евклидова структура будет и у касательного подпространства Kp0M.
Квадрат длины произвольного вектора подпространства Kp0M выражается формулой
(6) I(dr) = dr2 = Edu2+2Fdudv+Gdv2,
где
E = (ru0)2, F = ru0•rv0 , G = (rv0)2
— метрические коэффициенты базиса (ru0, rv0).
Координаты u и v на поверхности M будем также обозначать u1 и u2 соответственно. Тогда
I(dr) = aabdua dub, a,b=1,2, (6)
где метрический тензор aab определяется формулами
aab = ra•rb, (a, b = 1,2)
Квадратичная форма (6) называется первой квадратичной формой поверхности M .
Длина кривой поверхности X определяется формулой
 s = ∫√(Eu¢2(t)+2Fu¢(t)v¢(t)+Gv¢2(t)) dt
s = ∫√(Eu¢2(t)+2Fu¢(t)v¢(t)+Gv¢2(t)) dt
Косинус угла между векторами
dr = r1du1 + r2du2 и dr = r1du1 + r2du2
определяется формулой
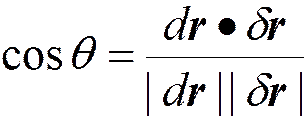 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|