
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конус второго порядка
Конус второго порядка
Исследуем уравнение поверхности
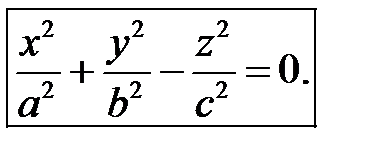 (35)
(35)
Пересечем поверхность (35) плоскостями 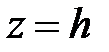 . Линия пересечения
. Линия пересечения 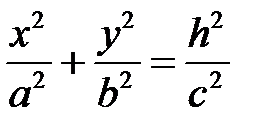 ,
, 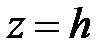 . При
. При 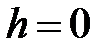 она вырождается в точку
она вырождается в точку 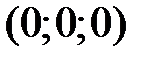 . При
. При 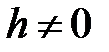 в сечении будем получать эллипсы
в сечении будем получать эллипсы
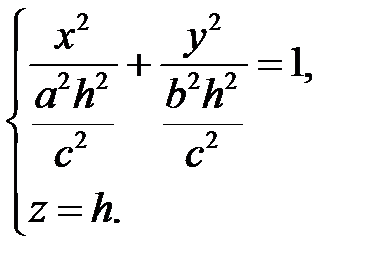
Полуоси этих эллипсов будут возрастать при возрастании 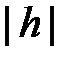 .
.
Рассечем поверхность (35) плоскостью 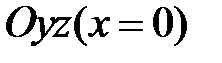 . Получится линия
. Получится линия
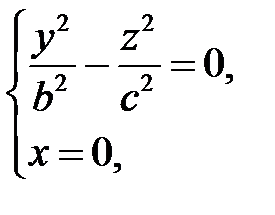
распадающаяся на две пересекающиеся прямые
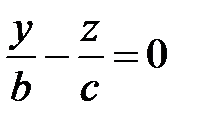 и
и 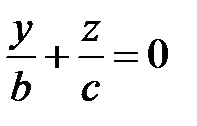 .
.
При пересечении поверхности (35) плоскостью 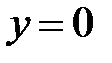 получим линию
получим линию
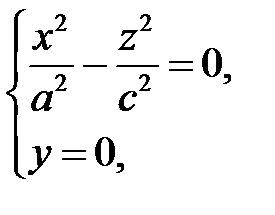
также распадающуюся на две пересекающиеся прямые
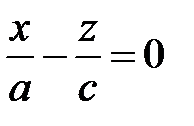 и
и 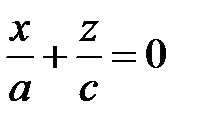 .
.
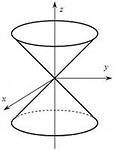
Поверхность, определяемая уравнением (35), называется конусом второго порядка.
Поверхности, составленные из прямых линий, называются линейчатыми. Такими поверхностями являются цилиндрические, конические поверхности, а также однополостный гиперболоид и гиперболический параболоид.
Пример 1. Найти центр и радиус сферы, заданной уравнением
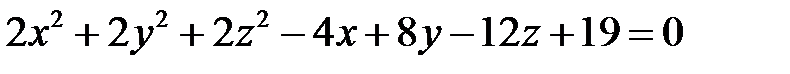 .
.
Разделим почленно данное уравнение на 2 и выделим полные квадраты:
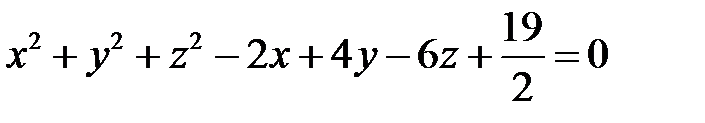 ,
,
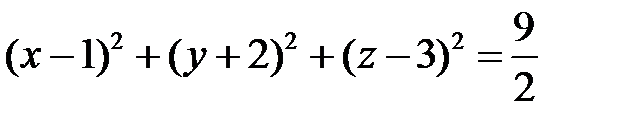 .
.
Перейдем к новым координатам по формулам
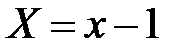 ;
; 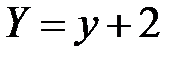 ;
; 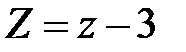 .
.
В новой системе координат уравнение принимает вид
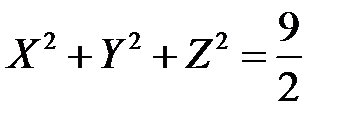 .
.
Оно определяет сферу радиуса 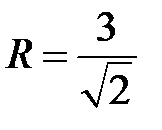 с центром в точке, для которой
с центром в точке, для которой 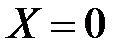 ;
; 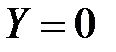 ;
; 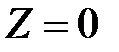 или
или 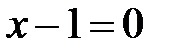 ;
; 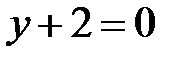 ;
; 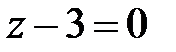 , т. е.
, т. е. 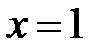 ;
; 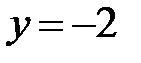 ;
; 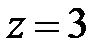 .
.
Следовательно, центр данной сферы находится в точке 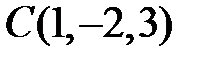 и радиус
и радиус 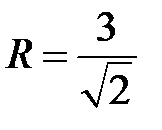 .
.
З а м е ч а н и е. Если уравнение
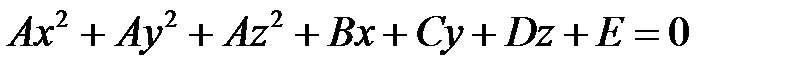
(т. е. уравнение, у которого коэффициенты при квадратах координат равны между собой, а коэффициенты при произведениях координат равны нулю) определяет некоторую поверхность, то этой поверхностью является сфера.
Уравнение (5.31) в этом случае может быть приведено к виду
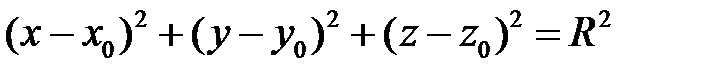 .
.
Уравнение (5.31) является уравнением сферы радиуса 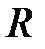 с центром в точке
с центром в точке 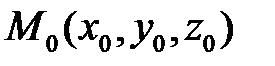 .
.
Пример 2. Определить вид и параметры поверхности, заданной уравнением
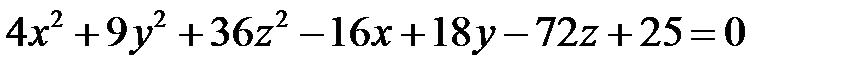 .
.
Вынося за скобки коэффициенты при квадратах координат и преобразуя уравнение, получаем
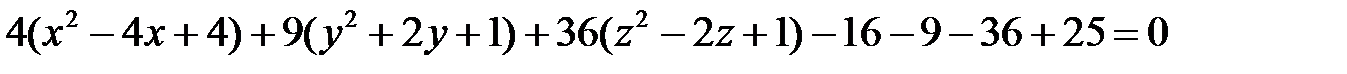 ,
,
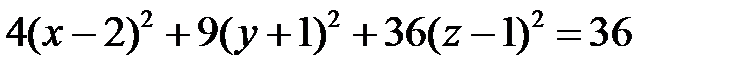 .
.
В новой системе координат
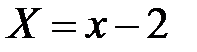 ;
; 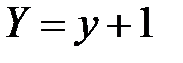 ;
; 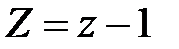
это уравнение принимает вид
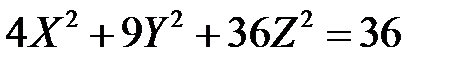
или
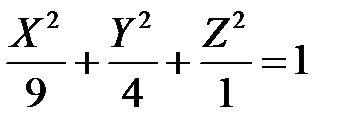 .
.
Сравнивая полученное уравнение с уравнением (5.6), заключаем, что оно определяет эллипсоид, параметры которого 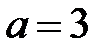 :
: 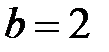 ,
, 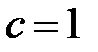 .
.
Центр эллипсоида находится в точке 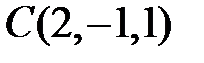 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|