Хелпикс

Главная

Контакты

Случайная статья



Эллиптический параболоид. Гиперболический параболоид

⇐ ПредыдущаяСтр 5 из 6Следующая ⇒


Эллиптический параболоид

Исследуем поверхность, заданную уравнением

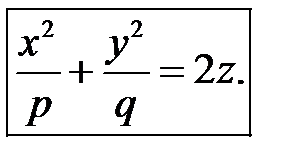                                                                                  (33)

где 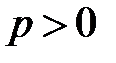, 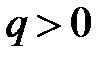. Рассечем поверхность (33) плоскостями 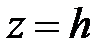. В сечении получим линию, уравнения которой есть

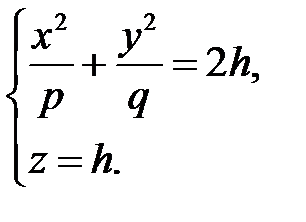
Если 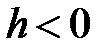, то плоскости  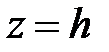поверхности не пересекают; если 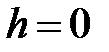, то плоскость  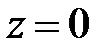касается поверхности в точке 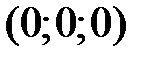; если 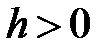, то в сечении имеем эллипс, уравнение которого имеет вид

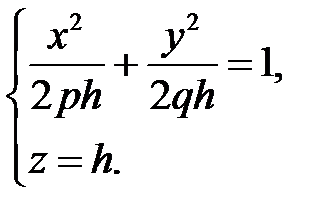
Его полуоси возрастают с ростом .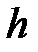

При пересечении поверхности (33) координатными плоскостями 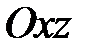 и 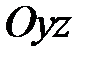получатся соответственно параболы  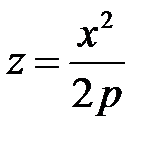и 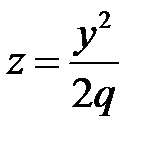. Таким образом, поверхность, определяемая уравнением (33), имеет вид выпуклой, бесконечно расширяющейся чаши. Поверхность (33) называется эллиптическим параболоидом.

 

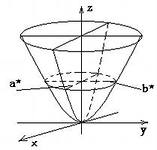
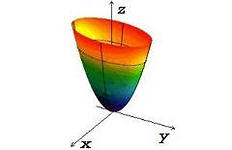
Гиперболический параболоид

Исследуем поверхность, определяемую уравнением

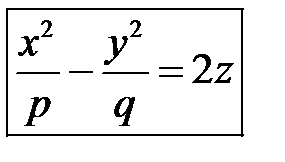                                                                                  (34)

где 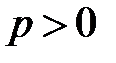, 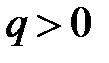. Рассечем поверхность (34) плоскостями 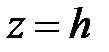. Получим кривую

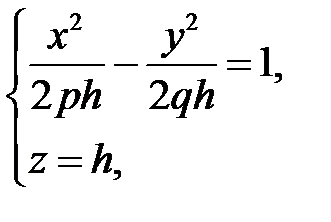
которая при всех значениях 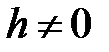 является гиперболой. При  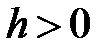ее действительные оси параллельны ос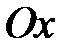и ; при 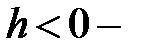параллельны ос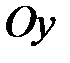и ; при 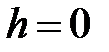 линия пересечения  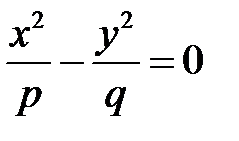распадается на пару пересекающихся прямых  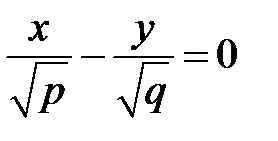и 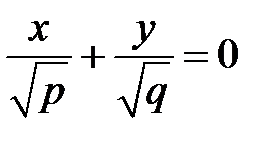. При пересечении поверхности плоскостями, параллельными плоскости 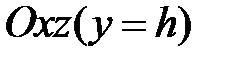, будут получаться параболы

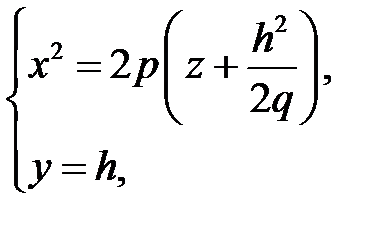
ветви которых направлены вверх. При 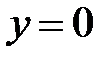 в сечении получается парабола

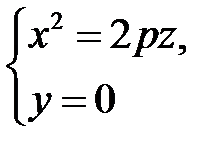
с вершиной в начале координат и осью симметрии .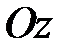

Пересекая поверхность (34) плоскостями 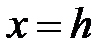, получим параболы 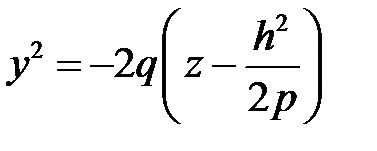, ветви которых направлены вниз.

 

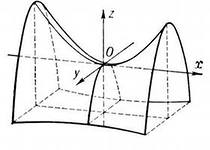
Анализ линии пересечения позволяет определить вид поверхности: она имеет вид седла. Поверхность (34) называется гиперболическим параболоидом.


⇐ Предыдущая123456Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.