
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Поверхности в пространстве
Поверхности в пространстве
Поверхность, образованная движением прямой 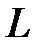 , которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую
, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую 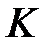 , называется цилиндрической поверхностью или цилиндром. При этом прямая
, называется цилиндрической поверхностью или цилиндром. При этом прямая 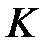 называется направляющей цилиндра, а прямая
называется направляющей цилиндра, а прямая 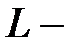 его образующей.
его образующей.
Будем рассматривать цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой плоскости.
Пусть в плоскости 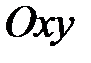 лежит некоторая линия
лежит некоторая линия 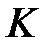 , уравнение которой
, уравнение которой
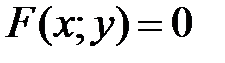 . (21)
. (21)
Построим цилиндр с образующими параллельными оси 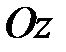 и направляющей
и направляющей 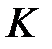 .
.
Теорема. Уравнение цилиндра, образующие которого параллельны оси 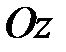 , имеет вид (21), т. е. не содержит координаты
, имеет вид (21), т. е. не содержит координаты 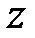 .
.
Возьмем на цилиндре любую точку 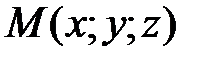 . Она лежит на какой-то образующей. Пусть
. Она лежит на какой-то образующей. Пусть 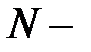 точка пересечения этой образующей с плоскостью
точка пересечения этой образующей с плоскостью 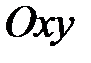 . Следовательно, точка
. Следовательно, точка 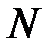 лежит на кривой
лежит на кривой 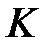 и ее координаты удовлетворяют уравнению (21).
и ее координаты удовлетворяют уравнению (21).
Но точка 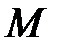 имеет такие же абсциссу
имеет такие же абсциссу 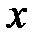 и ординату
и ординату 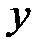 , что и точка
, что и точка 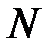 . Следовательно, уравнению (21) удовлетворяют и координаты точки
. Следовательно, уравнению (21) удовлетворяют и координаты точки 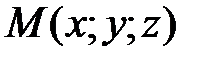 , так как оно не содержит
, так как оно не содержит 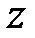 . И так как
. И так как 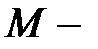 это любая точка цилиндра, то уравнение (21) и будет уравнением этого цилиндра.
это любая точка цилиндра, то уравнение (21) и будет уравнением этого цилиндра.
Теперь ясно, что 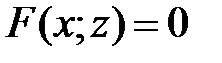 есть уравнение цилиндра с образующими, параллельными оси
есть уравнение цилиндра с образующими, параллельными оси 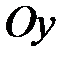 , а
, а 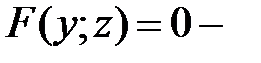 с образующими, параллельными оси
с образующими, параллельными оси 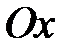 . Название цилиндра определяется названием направляющей. Если направляющей служит эллипс
. Название цилиндра определяется названием направляющей. Если направляющей служит эллипс
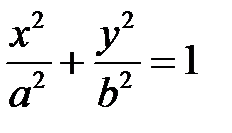
в плоскости 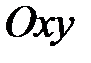 , то соответствующая цилиндрическая поверхность называется эллиптическим цилиндром.
, то соответствующая цилиндрическая поверхность называется эллиптическим цилиндром.
Частным случаем эллиптического цилиндра является круговой цилиндр, его уравнение 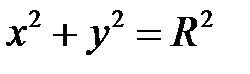 . Уравнение
. Уравнение 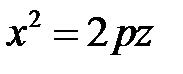 определяет в пространстве параболический цилиндр. Уравнение
определяет в пространстве параболический цилиндр. Уравнение
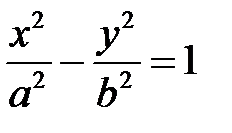
определяет в пространстве гиперболический цилиндр.
Все эти поверхности называются цилиндрами второго порядка, так как их уравнения есть уравнения второй степени относительно текущих координат 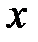 ,
, 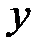 и
и 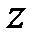 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|