
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Поверхности вращения. Конические поверхности
Поверхности вращения. Конические поверхности
Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая 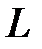 лежит в плоскости
лежит в плоскости 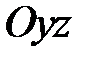 . Уравнения этой кривой запишутся в виде
. Уравнения этой кривой запишутся в виде
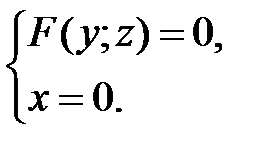 (22)
(22)
Найдем уравнение поверхности, образованной вращением кривой 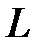 вокруг оси
вокруг оси 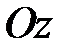 .
.
Возьмем на поверхности произвольную точку 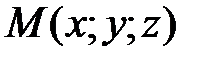 . Проведем через точку
. Проведем через точку 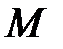 плоскость, перпендикулярную оси
плоскость, перпендикулярную оси 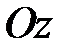 , и обозначим точки пересечения ее с осью
, и обозначим точки пересечения ее с осью 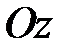 и кривой
и кривой 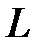 соответственно через
соответственно через 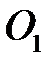 и
и 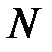 . Обозначим координаты точки
. Обозначим координаты точки 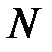 через
через 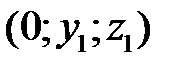 . Отрезки
. Отрезки 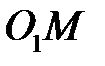 и
и 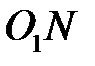 являются радиусами одной и той же окружности. Поэтому
являются радиусами одной и той же окружности. Поэтому 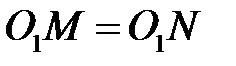 . Но
. Но 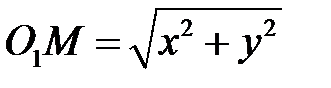 ,
, 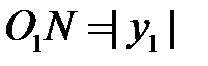 . Следовательно,
. Следовательно, 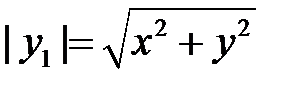 или
или 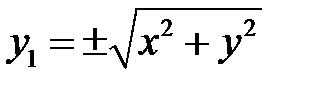 . Кроме того, очевидно,
. Кроме того, очевидно, 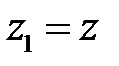 .
.
Так как точка 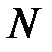 лежит на кривой
лежит на кривой 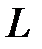 , то ее координаты удовлетворяют уравнению (22). Стало быть,
, то ее координаты удовлетворяют уравнению (22). Стало быть, 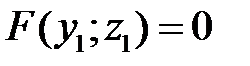 . Исключая вспомогательные координаты
. Исключая вспомогательные координаты 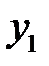 и
и 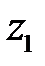 точки
точки 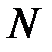 , приходим к уравнению
, приходим к уравнению
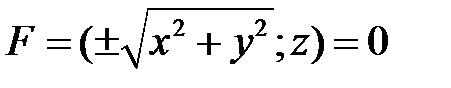 . (23)
. (23)
Уравнение (23) — искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точки М этой поверхности и не удовлетворяют координаты точек, не лежащих на поверхности вращения.
Как видно, уравнение (23) получается из (22) простой заменой 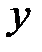 на
на 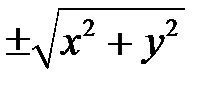 , координата
, координата 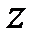 сохраняется.
сохраняется.
Понятно, что если кривая (22) вращается вокруг оси 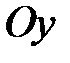 , то уравнение поверхности вращения имеет вид
, то уравнение поверхности вращения имеет вид
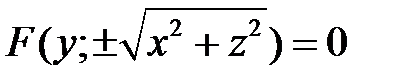 ;
;
если кривая лежит в плоскости 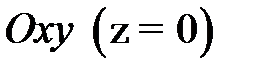 и ее уравнение
и ее уравнение 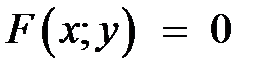 , то уравнение поверхности вращения, образованной вращением кривой вокруг оси
, то уравнение поверхности вращения, образованной вращением кривой вокруг оси 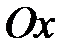 , есть
, есть 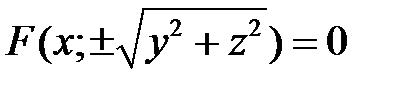 .
.
Так, например, вращая прямую 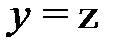 вокруг оси
вокруг оси 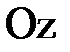 , получим поверхность вращения (ее уравнение
, получим поверхность вращения (ее уравнение 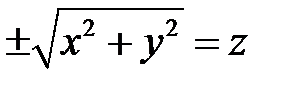 или
или 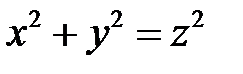 ). Она называется конусом второго порядка.
). Она называется конусом второго порядка.
Поверхность, образованная прямыми линиями, проходящими через данную точку 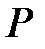 и пересекающими данную плоскую линию
и пересекающими данную плоскую линию 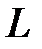 (не проходящую через
(не проходящую через 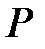 ), называется конической поверхностью или конусом. При этом линия
), называется конической поверхностью или конусом. При этом линия 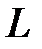 называется направляющей конуса, точка
называется направляющей конуса, точка 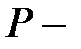 ее вершиной, а прямая, описывающая поверхность, называется образующей.
ее вершиной, а прямая, описывающая поверхность, называется образующей.
Пусть направляющая 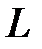 задана уравнениями
задана уравнениями
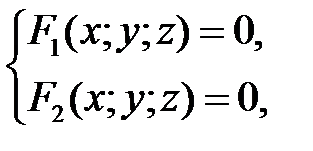 (24)
(24)
а точка 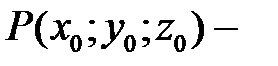 вершина конуса. Найдем уравнение конуса.
вершина конуса. Найдем уравнение конуса.
Возьмем на поверхности конуса произвольную точку 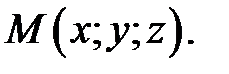 Образующая, проходящая через точки
Образующая, проходящая через точки 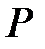 и
и 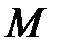 , пересечет направляющую
, пересечет направляющую 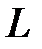 в некоторой точке
в некоторой точке 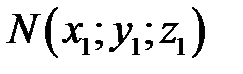 . Координаты точки
. Координаты точки 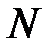 удовлетворяют уравнениям (24) направляющей:
удовлетворяют уравнениям (24) направляющей:
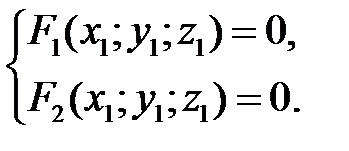 (25)
(25)
Канонические уравнения образующих, проходящих через точки 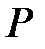 и
и 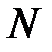 , имеют вид
, имеют вид
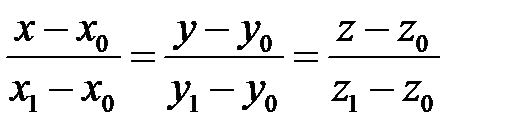 . (26)
. (26)
Исключая 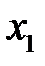 ,
, 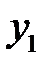 и
и 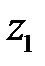 из уравнений (25) и (26), получим уравнение конической поверхности, связывающее текущие координаты
из уравнений (25) и (26), получим уравнение конической поверхности, связывающее текущие координаты 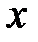 ,
, 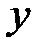 и
и 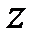 .
.
Пример. Составить уравнение конуса с вершиной в точке 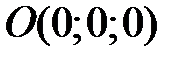 , если направляющей служит эллипс
, если направляющей служит эллипс 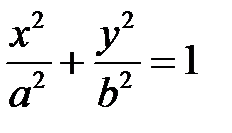 , лежащий в плоскости
, лежащий в плоскости 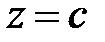 .
.
Решение: Пусть 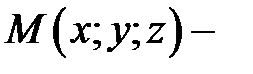 любая точка конуса. Канонические уравнения образующих, проходящих через точки
любая точка конуса. Канонические уравнения образующих, проходящих через точки 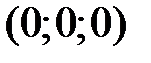 и точку
и точку 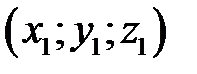 пересечения образующей
пересечения образующей 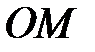 с эллипсом будут
с эллипсом будут 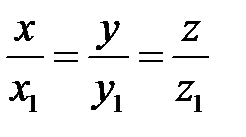 . Исключим
. Исключим 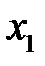 ,
, 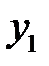 и
и 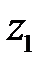 из этих уравнений и уравнения
из этих уравнений и уравнения
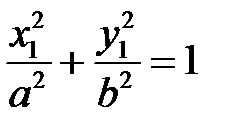 (27)
(27)
(точка 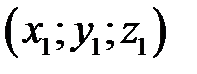 лежит на эллипсе),
лежит на эллипсе), 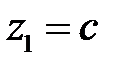 . Имеем,
. Имеем, 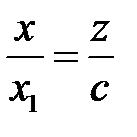 ,
, 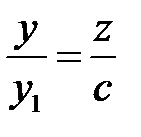 . Отсюда
. Отсюда 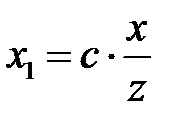 и
и 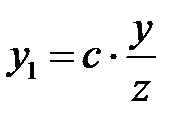 . Подставляя значения
. Подставляя значения 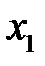 и
и 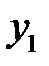 в уравнение эллипса (27), получим
в уравнение эллипса (27), получим
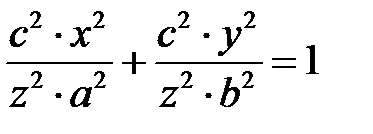 или
или 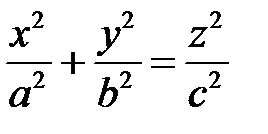 .
.
Это и есть искомое уравнение конуса.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|