Хелпикс

Главная

Контакты

Случайная статья



Найдем седловую точку S( x10, x20, l10 , l20, l30 ) , используя решение задачи, полученное графически.

⇐ ПредыдущаяСтр 5 из 5


Найдем   седловую точку   S( x10, x20, l10 , l20, l30 ) , используя решение задачи, полученное графически.

Графически получено оптимальное решение в точке М (4 ; 3 ) поэтому

 

S( 4 , 3 , l10 , l20, l30 ).

 

Для вычисления l10 , l20, l3  запишем функцию Лагранжа F(x,l).

F(x,l)= 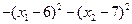   +l1(  ) +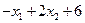

                                                                   

                                                                        + l2( ) +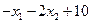

                                                                       

                                                                         + l3(  )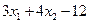                                                                         

 

Локальные условия Куна-Таккера:

 

              

                                                   

 

 

 

                                

 

 

 

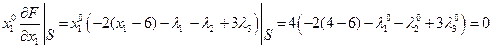
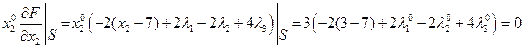
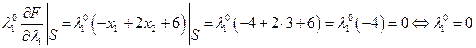
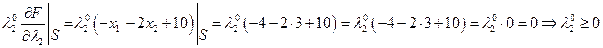
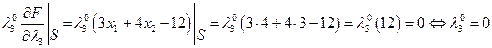
Подставим 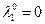 и 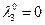 в 1-е и 2-е уравнения:

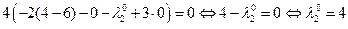
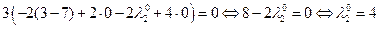
Седловая точка функции Лагранжа: S .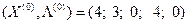

 

           Проверим условия cедловой точки:

 

 

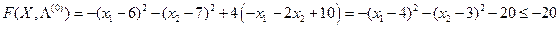
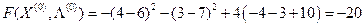
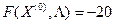
           Условия  (*) выполнены.

 

Ответ:  S 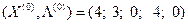– седловая точка.

 

91 - 100. Для двух предприятий выделено  единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим. если известно, что доход от x единиц, вложенных в первое предприятие, равен , а доход от  единиц, вложенных во второе предприятие, равен . Остаток средств к концу года составляет  для первого предприятия и  - для второго предприятия. Решить задачу методом динамического программирования.   

 

№ зад.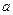
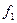
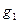
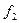
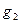
100. 3 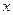0,6 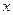4 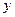0,4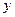

Решение. Процесс распределения средств разобъем на 4 этапа – по соответствующим годам.

 Пусть i  - сумма средств выделенных предприятиям в i-м году, xi - средства вложенные в первое предприятие в i-м году, yi – средства вложенные во второе предприятие в i-м году, тогда

 

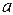i = xi 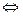+ yi      yi = 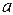i - xi

Остаток средств от обоих предприятий на i–ом шаге:

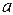i+1 = g1 (xi ) + g2 (yi ) =g1 (xi ) + g2 (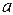i - xi) = 0,6 xi   + 0,4 (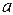i - xi) = 0,2xi   + 0,4 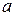i          

 

Пусть Fi – cуммарный  наибольший общий доход от обоих предприятий в i-м и последующих годах, тогда

 

Fi =  =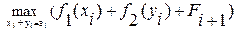

= =

 

=

 

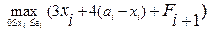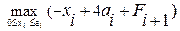
Пусть i = 5 тогда по условию F5 = 0.

i = 4, F4 = = = ,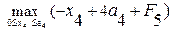

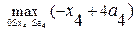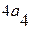 т.к. линейная убывающая функция достигает наибольшего значения в начале рассматриваемого промежутка 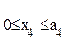, т.е. при .

 

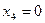i = 3, F3 = = =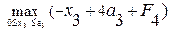

 

= ,

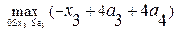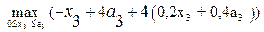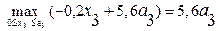т.к. линейная убывающая функция достигает наибольшего значения в начале 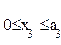 промежутка, т.е. при .

 

 

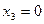i = 2, F2 = =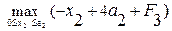

 

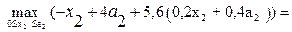
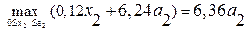, т.к. линейная возрастающая функция достигает наибольшего значения в конце рассматриваемого промежутка, т.е. при .

 

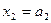i = 1, F1 = =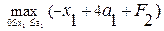

 

 

 

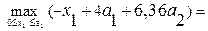
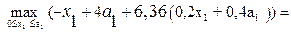
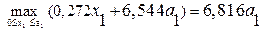
т.к. линейная возрастающая функция достигает наибольшего значения в конце рассматриваемого промежутка, т.е. при .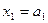

 

Итак наибольший общий доход   F1 = =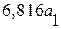

 

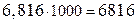
Составим оптимальное распределение средств по годам

 

Т.к. ,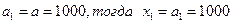

 

Далее получаем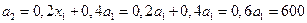

 

 

 

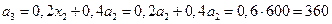
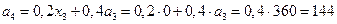
Остаток средств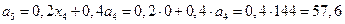

 

        Годы Предпр. Остаток
xi  

 

57,6
yi  

 

 


⇐ Предыдущая12345
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.