
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение. Согласно указанию 1) требуется минимизировать стоимость перевозок (суммарные затраты) S = S dijxij. Далее расстояние dij будем обозначать через cij и называть тарифом.
Решение. Согласно указанию 1) требуется минимизировать стоимость перевозок (суммарные затраты) S = S dijxij. Далее расстояние dij будем обозначать через cij и называть тарифом.
Первое базисное решение найдем по методу северо-западного угла.
 П
Б П
Б
| ai | |||||
7
  50 50
| 1
 40 40
| 7 | 4 | 9 | ||
| 4 | 3
 20 20
| 2 50 | 1
 0 0
| 5 | 2 | |
| 5 | 6 | 8 | 6 40 | 2 70 | 7 | |
| bj | 7 | 1 | 0 | -1 | -5 |
В клетку с тарифом d11 = c11 = 7 помещаем наибольший возможный груз x = 50 , далее выбираем клетку с тарифом 1 и помещаем туда груз 40 и т.д. При этом следим за тем, чтобы на каждом шаге, кроме последнего, из рассмотрения выбывали только одна строка или столбец, в противном случае в одном из выбывающих рядов ( в строке или в столбце) ставим ноль в клетку с наименьшим тарифом ( в данном случае в клетку (2, 4) с тарифом 1 ставим 0).
 Проверим является ли полученное базисное решение оптимальным с помощью метода потенциалов. Составим уравнения для всех базисных (загруженных) клеток:
Проверим является ли полученное базисное решение оптимальным с помощью метода потенциалов. Составим уравнения для всех базисных (загруженных) клеток:
cij = ai + bj (1)
Так как число уравнений m + n – 1 = 3 + 5 –1 = 7, а число потенциалов ai, bj равно m + n = 8, то пусть a1 = 0. Далее находим потенциалы из следствий уравнений (1):
bj = cij - ai или ai = cij - bj.

Результаты заносим в таблицу. Далее находим алгебраические суммы тарифов sij для всех свободных клеток из уравнений:
sij = cij – (ai + bj ) (2)
(Запишем только sij < 0, если есть)
s21 = 4 – (2+7)= - 5;
s31 = 5 – (7+7)= - 9; s32 = 6 – (7+1)= - 2.
Так как не все sij ³ 0, то базисное решение не является оптимальным.
Выбираем клетку ( 3 , 1 ) с наименьшей из отрицательных алгебраических сумм тарифов - 9 и строим цикл пересчета для получения нового базисного решения.

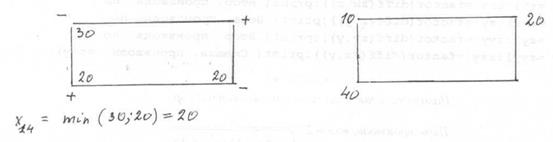
Перераспределяемый груз xij = min ( 50; 20; 40 ) = 20
 Запишем новое базисное решение в таблицу и проделаем процедуру пункта
Запишем новое базисное решение в таблицу и проделаем процедуру пункта  до тех пор пока не получим для всех свободных клеток sij ³ 0.
до тех пор пока не получим для всех свободных клеток sij ³ 0.
 П
Б П
Б
| ai | |||||
7
  30 30
| 1 60 | 7 |  4 4
| 9 | ||
| 4 | 3 | 2 50 | 1 20 | 5 | -7 | |
5
 20 20
| 6 | 8 | 6 20 | 2 70 | - 2 | |
| bj | 7 | 1 | 9 | 8 | 4 |
s13 = 7 – (0+9)= - 2; s14 = 4 – (0+8)= - 4;
 П
Б П
Б
| ai | |||||
| 7 10 | 1 60 | 7 | 4 20 | 9 | ||
| 4 | 3 | 2 50 | 1 20 | 5 | -3 | |
| 5 40 | 6 | 8 | 6 | 2 70 | -2 | |
| bj | 7 | 1 | 5 | 4 | 4 |
Так как для всех свободных клеток sij ³ 0, то полученное базисное решение является оптимальным.
Наименьшие суммарные затраты Smin = S cijxij = 10 · 7 + 60 · 1 + 20 · 4 + 50 ·2 + 20 · 1 + 40 · 5 + 70 · 2 = 670
Замечание. Данное решение не является единственным , так как клетка (2, 1 ) имеет
s21 = 4 – (-3+7)= 0 .
- нулевая алгебраическая сумма тарифов.
С помощью цикла пересчета клетки (2, 1 ) можно получить еще одно оптимальное решение.
81 - 90. Дана задача выпуклого программирования. Требуется:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|