
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дадим геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами
Дадим геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами
 |
x1 + 2 x2 £ 32
3x1 + 3x2 £ 60
3x1 + x2 £ 50
xi ³ 0, i = 1,2.
F = 4x1 + 2x2 (max).
Оптимальное решение находим в точках выхода линий уровня из области D в направлении градиента функции F.
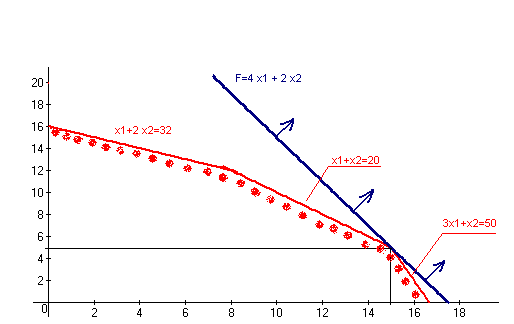
Ответ: план производства изделий А и В, обеспечивающий максимальную прибыль
денежных единиц от их реализации: изделий А - 15 штук и изделий В - 5 штук.
71 - 80. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2, А3 находится груз в количестве а1, а2, а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 - тонн груза. Расстояния в сотнях километров между пунктами поставки и потребления приведены в матрице-таблице D= (dij):
| Пункты поставки (базы – Б) | |||||
Пункты потребления
(потребители – П)
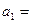 90,
90, 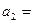 70,
70, 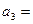 110,
110,
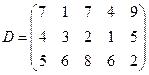
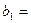 50,
50, 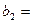 60,
60, 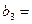 50,
50, 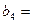 40,
40, 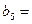 70.
70.