Хелпикс

Главная

Контакты

Случайная статья



найти решение графическим методом;

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒


   1) найти решение графическим методом;                     

   2) написать функцию Лагранжа данной задачи и найти ее седловую точку, используя решение задачи, полученное графически.                                                                      

8х. ,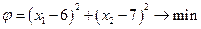
 

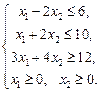
Решение. 1) найдем решение графическим методом.

 

 


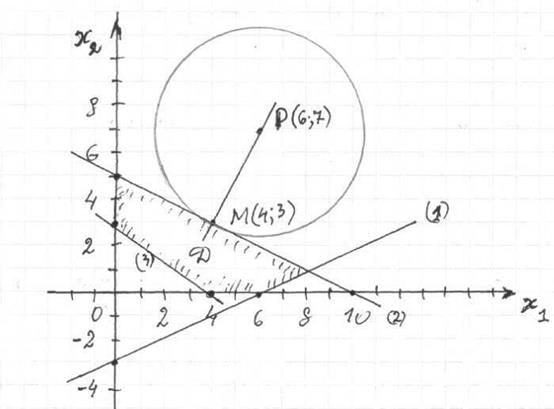
Система неравенств определяет область D допустимых значений, ограниченную тремя прямыми и координатными осями. График целевой функции j представляет собой окружность переменного радиуса с центром в точке P (6 , 7) (линии уровня целевой функции). Значение целевой функции графически представляет собой квадрат радиуса этой окружности. Минимальным радиусом, удовлетворяющим системе ограничений, будет такой радиус, который обеспечивает касание окружности с границей области так, как это показано на рисунке.     Точка М ( 4 ; 3 ) – точка входа линий уровня целевой функции в область D, поэтому jmin(М) =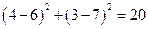

 

           Искомая точка M определяется при решении системы уравнений:

 

 

 

 

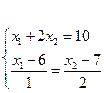
В этой системе 1-е уравнение определяет прямую (2), а 2-е – прямую, проходящую через точку P  перпендикулярно прямой  (2).

 

2) Запишем задачу в стандартном виде:

 

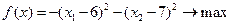
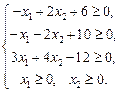
           Функция 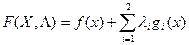 называется функцией Лагранжа, а переменные  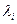- коэффициентами Лагранжа.

      Точка S 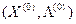 называется седловой точкой функции Лагранжа, если для любых  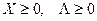выполняются неравенства:

 

                   (*)

 

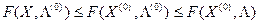Если функции 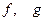 дифференцируемы, то условия, определяющие седловую точку (условия Куна-Таккера) следующие:

 

 

 


⇐ Предыдущая12345Следующая ⇒
  

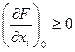
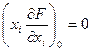
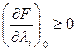
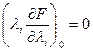
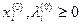
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.