Задание 2. Дифракция Фраунгофера на одномерной дифракционной решетке 2 страница
| Задание 2. 1. Вставьте в поворотный стол один из исследованных объектов (объект 4 или 5) и установите поворотный стол в начальное положение (нулевая координата). 2. Добейтесь максимальной поляризации света в вертикальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в вертикальное положение. | E излучения, прошедшего через поляризатор) установлена параллельно направлению рукоятки 1 шкалы поворотного держателя.
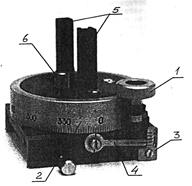 Рис. 12.
Модуль 13 (стол поворотный, рис.12) предназначен для установки объектов с возможностью поворота вокруг вертикальной оси, а также для отсчета угловых координат и углов поворота. Поворот стола производится ручкой 1. Отсчет угловых координат производится по основной шкале 2 (цена деления 20) и нониусу 3 (цена деления 0,50). Рычаг 4 поворачивают до совпадения его вертикальной риски с одним из делений основной шкалы и снимают отсчет по основной шкале. К полученному значению прибавляют отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10, при погрешности порядка 0,20. углы поворота определяют как разности угловых координат. Объекты вставляют в кронштейны 5; винтом 6 регулируют наклон платформы стола и установленного на столе объекта.
Набор объектов
При выполнении лабораторных работ помимо функциональных модулей используется также ряд объектов. Большая часть объектов – тонкие пластины, пленки или линзы, расположенные в средней плоскости соответствующего экрана. При установке экрана в кассету функционального модуля эта плоскость оказывается напротив риски рейтера или иной характерной отметки на модуле. Тем самым определяется координата объекта на оптической скамье.
Рис. 12.
Модуль 13 (стол поворотный, рис.12) предназначен для установки объектов с возможностью поворота вокруг вертикальной оси, а также для отсчета угловых координат и углов поворота. Поворот стола производится ручкой 1. Отсчет угловых координат производится по основной шкале 2 (цена деления 20) и нониусу 3 (цена деления 0,50). Рычаг 4 поворачивают до совпадения его вертикальной риски с одним из делений основной шкалы и снимают отсчет по основной шкале. К полученному значению прибавляют отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10, при погрешности порядка 0,20. углы поворота определяют как разности угловых координат. Объекты вставляют в кронштейны 5; винтом 6 регулируют наклон платформы стола и установленного на столе объекта.
Набор объектов
При выполнении лабораторных работ помимо функциональных модулей используется также ряд объектов. Большая часть объектов – тонкие пластины, пленки или линзы, расположенные в средней плоскости соответствующего экрана. При установке экрана в кассету функционального модуля эта плоскость оказывается напротив риски рейтера или иной характерной отметки на модуле. Тем самым определяется координата объекта на оптической скамье.
| |
Так как при прохождении через поляризатор свет полностью поляризуется, то при вращении пластинки в горизонтальной плоскости на экране можно заметить, что при некотором значении угла поворота интенсивность света должна быть минимальной. Такое значение угла поворота и есть угол Брюстера, т. е. свет практически не отражается, а точнее отражается лишь та часть свет, в котором колебания вектора 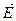 не параллельны плоскости падения (горизонтальная плоскость), т. к. поляризатор неидеальный. Найденный угол и будет являться углом Брюстера.
Эксперимент
1. Установка оборудования.
Для проведения работы, необходимо установить на оптической скамье модуль 12, представляющий собой поляризатор с нониусом, модуль 13 – стол поворотный, в который установлена плоскопараллельная пластинка (объект 4)) последовательно друг за другом.
2. Калибровка установки.
После установки приборов необходимо произвести калибровку установки. Сначала при помощи ручки 1 (рис. ) поворотного стола устанавливают его на нулевую угловую координату, рычаг 4 поворачивают до совпадения его вертикальной риски с нулевым делением основной шкалы.
Затем двумя передними винтами 6 и двумя задними винтами 2 излучателя (рис. ) добиваются совпадение падающего и отраженного света (отраженный свет должен попасть в трубку излучателя).
Так определяется положение нормали к пластинке.
3. Измерения.
Задание 1.
1. Добейтесь максимальной поляризации света в горизонтальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в горизонтальное положение так, чтобы нулевая координата оси поляризатора была напротив риски нониуса. не параллельны плоскости падения (горизонтальная плоскость), т. к. поляризатор неидеальный. Найденный угол и будет являться углом Брюстера.
Эксперимент
1. Установка оборудования.
Для проведения работы, необходимо установить на оптической скамье модуль 12, представляющий собой поляризатор с нониусом, модуль 13 – стол поворотный, в который установлена плоскопараллельная пластинка (объект 4)) последовательно друг за другом.
2. Калибровка установки.
После установки приборов необходимо произвести калибровку установки. Сначала при помощи ручки 1 (рис. ) поворотного стола устанавливают его на нулевую угловую координату, рычаг 4 поворачивают до совпадения его вертикальной риски с нулевым делением основной шкалы.
Затем двумя передними винтами 6 и двумя задними винтами 2 излучателя (рис. ) добиваются совпадение падающего и отраженного света (отраженный свет должен попасть в трубку излучателя).
Так определяется положение нормали к пластинке.
3. Измерения.
Задание 1.
1. Добейтесь максимальной поляризации света в горизонтальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в горизонтальное положение так, чтобы нулевая координата оси поляризатора была напротив риски нониуса.
| | | Объект №1 – сетка с шагом 1 мм, используется для калибровки увеличения оптических устройств.
Объект № 5 – плоскопараллельная стеклянная пластина толщиной 4-8 мм. Точное значение толщины указывается в описании работы или определяется самостоятельно.
Объекты № 15-24 и 27-36 – пленки с определенным распределением коэффициента пропускания. Качество пленок соответствует требованиям голографии. Пленки чувствительны к механическим воздействиям и их нельзя трогать пальцами.
Объект № 25 – раздвижная щель.
Объект №38 – фотодатчик, содержит фотодиод в светонепроницаемой оправе с входным окном. Датчик установлен на стандартном экране размерами 40Х80 мм, который вставляется в кронштейны поворотного стола, при этом окно датчика оказывается на уровне оптической оси установки. Фототок измеряют в режиме «короткого замыкания» датчика.
Объект № 39 – пластина слюды толщиной 30 – 60 мкм. В плоскости пластины находятся две главные оси кристалла, соответствующие показателям преломления n1=1,59, n2=1,594.
Объект №44 – кювета для жидкостей. Предназначена для изучения оптических явлений при прохождении света через жидкость. Длина столба жидкости равна 120 мм. Для заполнения жидкостью отворачивают крышку кюветы, снимают защитное стекло и наливают жидкость так, чтобы получить слегка выпуклый мениск. Затем кладут стекло на мениск и завинчивают без воздушных пузырей.
Объект № 45 – свободный экран, в который можно установить интересующий объект. Белая наклейка со шкалой служит экраном при наблюдениях в прямом пучке лазера.
Настройка установки
Настройка заключается в фиксации лазерного луча и центров оптических элементов на оптической оси установки, расположенной на высоте 40 мм от верхней плоскости рейтеров. Совместную настройку группы оптических элементов называют юстировкой. Индикатором | |
результате действия на них 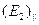 . Вместе с тем . Вместе с тем 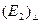 будет раскачивать электроны в направлении, перпендикулярном к плоскости падения, и такое излучение будет распространяться без всяких ограничений в направлении, удовлетворяющей условию (9.5), целиком определяя поляризацию отраженной волны.
Порядок выполнения работы
Для экспериментального определения угла Брюстера пользуются тем, что при некотором значении угла падения от границы раздела двух диэлектриков отразится только электромагнитная волна с такой поляризацией, в которой колебания вектора будет раскачивать электроны в направлении, перпендикулярном к плоскости падения, и такое излучение будет распространяться без всяких ограничений в направлении, удовлетворяющей условию (9.5), целиком определяя поляризацию отраженной волны.
Порядок выполнения работы
Для экспериментального определения угла Брюстера пользуются тем, что при некотором значении угла падения от границы раздела двух диэлектриков отразится только электромагнитная волна с такой поляризацией, в которой колебания вектора 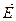 параллельны плоскости падения. В нашем эксперименте это горизонтальная плоскость, т. е. нужно добиться чтобы вектор параллельны плоскости падения. В нашем эксперименте это горизонтальная плоскость, т. е. нужно добиться чтобы вектор 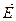 колебался именно в этой плоскости падения. Так как плоскость колебаний вектора колебался именно в этой плоскости падения. Так как плоскость колебаний вектора 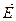 параллельна оси рукоятки излучателя, с помощью которой лазер поворачивается вокруг оптической оси, то нужно установить ее в горизонтальное положение, тем самым вектор параллельна оси рукоятки излучателя, с помощью которой лазер поворачивается вокруг оптической оси, то нужно установить ее в горизонтальное положение, тем самым вектор 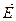 становится максимально поляризованным в горизонтальной плоскости, а чтобы добиться полной поляризации вектора становится максимально поляризованным в горизонтальной плоскости, а чтобы добиться полной поляризации вектора 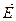 в этой плоскости, устанавливают за излучателем поляризатор, плоскость поляризации которого также должна быть горизонтальной (рис. 9.6). в этой плоскости, устанавливают за излучателем поляризатор, плоскость поляризации которого также должна быть горизонтальной (рис. 9.6).
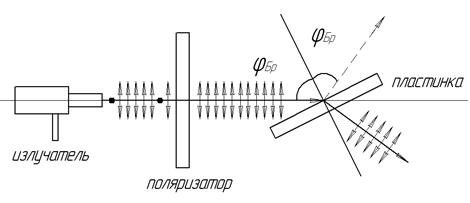 Рис. 9.6. Схема установки. Колебания вектора
Рис. 9.6. Схема установки. Колебания вектора 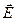 в плоскости падения условно обозначены стрелками, колебания, перпендикулярные плоскости пдания – точками. в плоскости падения условно обозначены стрелками, колебания, перпендикулярные плоскости пдания – точками.
| | | юстировки является микропроектор. Положение оптической оси после юстировки определяется положением центра линзы микропроектора.
Грубая юстировка. Поворотом винтов на корпусе лазера установите трубу с лазером в средней части корпуса и направьте пучок излучения вдоль оптической скамьи.
Точная юстировка. Установите микропроектор в положение с координатой риски 10,0 см, при этом точка выхода пучка после отражения от зеркала будет иметь координату 13,0 см и окажется напротив левого визирного креста экрана. Поворотом передних – считая от точки испускания излучения – винтов лазера совместите центр светового пятна с визирным крестом на экране. Отодвиньте микропроектор до положения с координатой риски 67,0 см, при этом точка выхода пучка после отражения от зеркала будет иметь координату 70,0 см и окажется напротив правого визирного креста экрана. Поворотом задних винтов излучателя совместите центр светового пятна с центром визирного креста. Операцию точной юстировки повторите 2-3 раза, пока смещение светового пятна от номинального положения при перемещении микропроектора не окажется меньше радиуса этого пятна.
При установке на рельс каждого нового оптического элемента прежде всего, с помощью винтов держателя этого элемента, добивайтесь возвращения центра пятна на экране в то же место, что и при юстировке лазерного луча. Это означает, что центр оптического элемента находится на оптической оси установки, и можно приступать к эксперименту или размещать на рельсе следующие элементы. В процессе эксперимента можно, смещая элементы винтами двухкоординатных держателей, перемещать картину на экране в положение, удобное для наблюдений или измерений.
Лабораторная работа №1
Измерение показателей преломления твердых тел
| |
Заметим, что отражение полностью поляризованной волны наблюдается тогда, когда нормали к преломленной и отраженной волнам взаимно перпендикулярны (рис. 9.4).
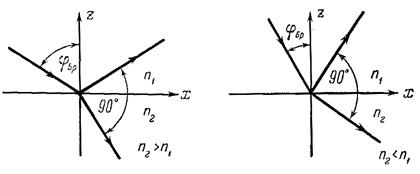 Рис. 9.4. Нормали к преломленной и ораженным волнам при падении света
на границу раздела двух сред под углом Брюстера перпендикулярны.
Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном к нормали к преломленной волне, не должна распространяться энергия, так как электрон не излучает в направлении, вдоль которого происходят его колебания (рис. 9.5).
Рис. 9.4. Нормали к преломленной и ораженным волнам при падении света
на границу раздела двух сред под углом Брюстера перпендикулярны.
Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном к нормали к преломленной волне, не должна распространяться энергия, так как электрон не излучает в направлении, вдоль которого происходят его колебания (рис. 9.5).
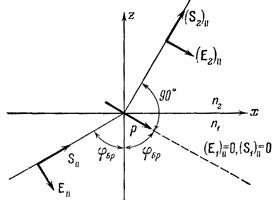 Рис. 9.5. К трактовке закона Брюстера с позиций электронной теории.
Вектор
Рис. 9.5. К трактовке закона Брюстера с позиций электронной теории.
Вектор  в падающей волне лежит в плоскости падения. Отраженная волна этой gоляризации отсутствует, т.к. электроны не излучают в направлении своих колебаний.
Легко заметить, что последнее ограничение относится лишь к колебаниям электронов в плоскости падения волны, происходящим в в падающей волне лежит в плоскости падения. Отраженная волна этой gоляризации отсутствует, т.к. электроны не излучают в направлении своих колебаний.
Легко заметить, что последнее ограничение относится лишь к колебаниям электронов в плоскости падения волны, происходящим в | | Цель работы: знакомство с устройством и работой лабораторного комплекса ЛКО-3П; ознакомление с методами определения показателей преломления прозрачных твердых тел.
Оборудование: модули: конденсор с экраном 5, объектив 6, микропроектор 2, поворотный стол 13; набор объектов: пластмассовая пластина 6, призма 9, стеклянная пластина 5.
Краткая теория
1.1. Общие сведения. Закон преломления и отражения света.
В геометрической оптике основным положением является приближение в котором длина волны света λ стремится к нулю. Причем световой поток в геометрической оптике считается совокупностью отдельных независимых световых лучей, каждый из которых подчиняется законам преломления и отражения света. В оптически изотропной среде лучи перпендикулярны к фронту волны в каждой точке фронта и описывают движение фронта световой волны в пространстве.
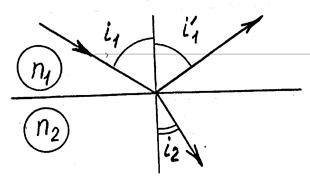 Рис. 1.1.
Доказательством прямолинейности распространения света служит образование тени. От точечного источника света возникает полная тень. Лучи, исходящие из одной точки, образуют расходящийся пучок (сечение пучка увеличивается). Лучи, сходящиеся в одну точку, образуют сходящийся пучок.
Рис. 1.1.
Доказательством прямолинейности распространения света служит образование тени. От точечного источника света возникает полная тень. Лучи, исходящие из одной точки, образуют расходящийся пучок (сечение пучка увеличивается). Лучи, сходящиеся в одну точку, образуют сходящийся пучок.
| |
вых, сразу видно, что если 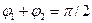 , то , то 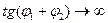 и, следовательно, и, следовательно, 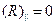 . Вместе с тем коэффициент отражения . Вместе с тем коэффициент отражения 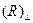 не обращается в нуль при не обращается в нуль при 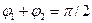 , так как знаменатель выражения (2.4) , так как знаменатель выражения (2.4) 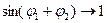 . Таким образом, получается, что при некотором значении угла падения от границы раздела отразится только электромагнитная волна с вполне определенной поляризацией. Волна, в которой колебания вектора . Таким образом, получается, что при некотором значении угла падения от границы раздела отразится только электромагнитная волна с вполне определенной поляризацией. Волна, в которой колебания вектора 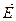 параллельны плоскости падения, вообще не отразится при параллельны плоскости падения, вообще не отразится при 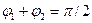 . Вектор . Вектор 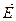 в отраженной волне (при выполнении условия в отраженной волне (при выполнении условия 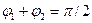 ) будет колебаться перпендикулярно к плоскости падения. В учебниках по оптике часто употребляют несколько иную терминологию. Так, например, в рассматриваемом случае говорят, что отраженный свет поляризован в плоскости падения. Отсюда видно, что плоскость поляризации света соответствует плоскости, перпендикулярной к направлению колебаний вектора ) будет колебаться перпендикулярно к плоскости падения. В учебниках по оптике часто употребляют несколько иную терминологию. Так, например, в рассматриваемом случае говорят, что отраженный свет поляризован в плоскости падения. Отсюда видно, что плоскость поляризации света соответствует плоскости, перпендикулярной к направлению колебаний вектора 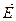 .
Для данного случая, впервые экспериментально обнаруженного Малю, очевидны следующие соотношения: если .
Для данного случая, впервые экспериментально обнаруженного Малю, очевидны следующие соотношения: если 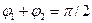 , то , то 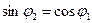 и, значит, и, значит,
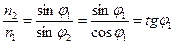 .
Эта зависимость угла, при котором наблюдается плоская поляризация отраженной волны, от отношения показателей преломления двух исследуемых диэлектриков носит название закона Брюстера, а соответствующий угол часто называют углом Брюстера .
Эта зависимость угла, при котором наблюдается плоская поляризация отраженной волны, от отношения показателей преломления двух исследуемых диэлектриков носит название закона Брюстера, а соответствующий угол часто называют углом Брюстера  . В этих обозначениях . В этих обозначениях
 . (9.5)
Для перехода световой волны (видимая область спектра) из воздуха в стекло . (9.5)
Для перехода световой волны (видимая область спектра) из воздуха в стекло  , что соответствует углу , что соответствует углу 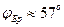 . .
| | При падении световой волны на плоскую границу раздела двух диэлектриков с разными значениями относительной диэлектрической проницаемости световая волна частично отражается и частично преломляется. Характеристиками сред в данном случае является скорость распространения света в них: 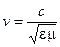 , где c= 3·108 м/с – скорость света в вакууме, ε – относительная диэлектрическая проницаемость среды, μ – относительная магнитная проницаемость среды (для подавляющего большинства диэлектрических сред , где c= 3·108 м/с – скорость света в вакууме, ε – относительная диэлектрическая проницаемость среды, μ – относительная магнитная проницаемость среды (для подавляющего большинства диэлектрических сред 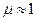 ). Отношение ). Отношение
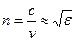 (1.1)
называется абсолютным показателем преломления света. Отношение (1.1)
называется абсолютным показателем преломления света. Отношение
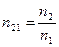 (1.2)
называется относительным показателем преломления света средой 2 по отношению к среде 1.
Формулы (1.1), (1.2) справедливы только для волн, частоты которых малы по сравнению с частотой процессов в атомах и молекулах среды. Вследствие дисперсии показателя преломления данные формулы справедливы лишь для монохроматических волн. Среды, в которых распространяются отраженная и преломленная волны, считаются полубесконечными, т.е. принимается, что на границе раздела сходятся только три волны: падающая, отраженная, преломленная, т.е. пренебрегают многократным отражением.
При падении световой волны на идеальную плоскую границу раздела 2-х диэлектриков, размеры которой значительно превышают длину волны, угол между направлением распространения отраженной волны и нормалью к границе раздела ι’1 (угол отражения) равен по абсолютной величине соответствующему углу для падающей волны ι1 (закон отражения, рис.1.1). Угол между направлением распространения преломленной волны и нормалью к границе раздела (угол преломления ι2) связан с углом падения законом преломления света: (1.2)
называется относительным показателем преломления света средой 2 по отношению к среде 1.
Формулы (1.1), (1.2) справедливы только для волн, частоты которых малы по сравнению с частотой процессов в атомах и молекулах среды. Вследствие дисперсии показателя преломления данные формулы справедливы лишь для монохроматических волн. Среды, в которых распространяются отраженная и преломленная волны, считаются полубесконечными, т.е. принимается, что на границе раздела сходятся только три волны: падающая, отраженная, преломленная, т.е. пренебрегают многократным отражением.
При падении световой волны на идеальную плоскую границу раздела 2-х диэлектриков, размеры которой значительно превышают длину волны, угол между направлением распространения отраженной волны и нормалью к границе раздела ι’1 (угол отражения) равен по абсолютной величине соответствующему углу для падающей волны ι1 (закон отражения, рис.1.1). Угол между направлением распространения преломленной волны и нормалью к границе раздела (угол преломления ι2) связан с углом падения законом преломления света:
| |
Последнее условие можно переписать в виде
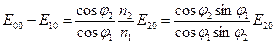 .
Отсюда легко получаются искомые зависимости .
Отсюда легко получаются искомые зависимости
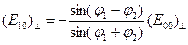 , , 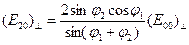 . (9.4)
Займемся анализом найденных соотношений. Прежде всего рассмотрим относительные интенсивности отраженной и преломленной волн. Проанализируем зависимость коэффициента отражения . (9.4)
Займемся анализом найденных соотношений. Прежде всего рассмотрим относительные интенсивности отраженной и преломленной волн. Проанализируем зависимость коэффициента отражения 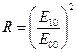 от угла падения (рис 9.3). от угла падения (рис 9.3).
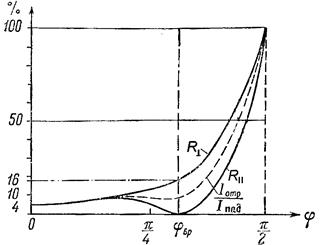 Рис.9.3. Зависимость коэффициента отражения R от угла падения
При переходе света из воздуха (n1»1) в стекло (n2»1,5).
Рассмотрение формул Френеля показывает, что компоненты
Рис.9.3. Зависимость коэффициента отражения R от угла падения
При переходе света из воздуха (n1»1) в стекло (n2»1,5).
Рассмотрение формул Френеля показывает, что компоненты 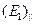 , и , и 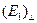 , по-разному изменяются с увеличением угла , по-разному изменяются с увеличением угла 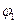 . Во-пер . Во-пер | | 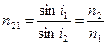 (1.3)
где n21 – относительный показатель преломления среды, в которой распространяется свет, относительно среды в которой распространяется падающий свет.
Если световая волна из оптически более плотной среды 1 падает на границу раздела с оптически менее плотной средой 2 (т.е. если (1.3)
где n21 – относительный показатель преломления среды, в которой распространяется свет, относительно среды в которой распространяется падающий свет.
Если световая волна из оптически более плотной среды 1 падает на границу раздела с оптически менее плотной средой 2 (т.е. если 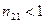 ), то при угле падения i1>iкр где siniкр=n21, величина sini2>1, что невозможно. Угол iкр при котором i2=900 и преломленная волна отсутствует, называется критическим углом падения света. Явления отражения света целиком в первую среду называется полным внутренним отражением света. Энергия падающей электромагнитной волны полностью возвращается в первую среду, но места захода падающей и выхода отраженной волны на границе раздела смещены друг относительно друга на расстояние порядка половины длины световой волны.
Отношение интенсивности отраженной волны к интенсивности падающей называется коэффициентом отражения света второй среды относительно первой. Отношение интенсивностей преломленной к интенсивности падающей волны называется коэффициентом пропускания второй среды относительно первой. ), то при угле падения i1>iкр где siniкр=n21, величина sini2>1, что невозможно. Угол iкр при котором i2=900 и преломленная волна отсутствует, называется критическим углом падения света. Явления отражения света целиком в первую среду называется полным внутренним отражением света. Энергия падающей электромагнитной волны полностью возвращается в первую среду, но места захода падающей и выхода отраженной волны на границе раздела смещены друг относительно друга на расстояние порядка половины длины световой волны.
Отношение интенсивности отраженной волны к интенсивности падающей называется коэффициентом отражения света второй среды относительно первой. Отношение интенсивностей преломленной к интенсивности падающей волны называется коэффициентом пропускания второй среды относительно первой.
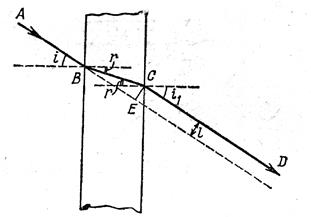 Рис. 1.2.
В геометрической оптике каждая точка источника света считается центром расходящегося
Рис. 1.2.
В геометрической оптике каждая точка источника света считается центром расходящегося
| |
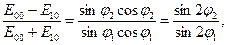
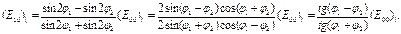 (9.2)
Складывая уравнения (2.1), получаем: (9.2)
Складывая уравнения (2.1), получаем:
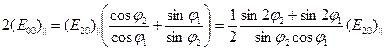 ,
откуда ,
откуда
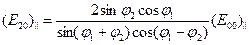 . (9.3)
2. Вектор . (9.3)
2. Вектор 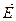 перпендикулярен к плоскости падения волны.
В этом случае выберем направление векторов перпендикулярен к плоскости падения волны.
В этом случае выберем направление векторов 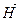 , ,  и и 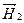 согласно рис. 9.2. На нем векторы согласно рис. 9.2. На нем векторы 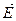 , , 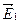 и и 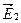 направлены от читателя перпендикулярно к плоскости чертежа. направлены от читателя перпендикулярно к плоскости чертежа.
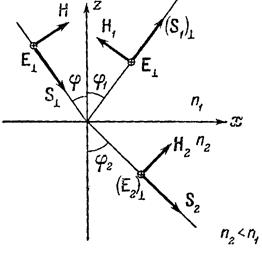 Рис. 9.2. Направления векторов
Рис. 9.2. Направления векторов 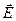 и и 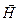 на границе раздела.
Вектор на границе раздела.
Вектор 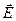 перпендикулярен плоскости падения луча.
Для проекций амплитуд исследуемых векторов на оси получим соотношения перпендикулярен плоскости падения луча.
Для проекций амплитуд исследуемых векторов на оси получим соотношения
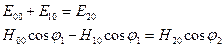
| | пучка лучей, называемого гомоцентрическим. Если после отражений и преломлений пучок сходится также в одну точку, то он тоже гомоцентрический. Центр отраженного или преломленного пучка называется изображением соответствующей точки источника света. Если каждой точке источника света соответствует одна точка изображения, то изображение называют стигматическим. Сходственные точки источника и изображения, а также соответствующие лучи и пучки света называются сопряженными. Задачей геометрической оптики является построение сопряженных изображений.
1.2. Прохождение света через плоскопараллельную пластинку.
Пусть луч АВ (рис.1.2) падает на плоскопараллельную стеклянную пластинку. В стекле он преломится и пойдет в направлении ВС. В точке С он снова преломится и выйдет из пластинки в направлении CD. Докажем, что луч CD, выходящий из пластинки, параллелен падающему на пластинку лучу АВ.
Для преломления в точке В имеем:
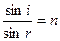 , (1.4)
где n – показатель преломления пластинки. Для преломления в точке С закон (1.3) дает: , (1.4)
где n – показатель преломления пластинки. Для преломления в точке С закон (1.3) дает:
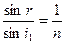 , (1.5)
так как в этом случае луч выходит из пластинки в воздух. Перемножив выражения (1.4) и (1.5), находим: , (1.5)
так как в этом случае луч выходит из пластинки в воздух. Перемножив выражения (1.4) и (1.5), находим:
 , (1.6)
или, так как ι<900 и i1<900, i=i1, откуда следует, что лучи АВ и CD параллельны.
Луч CD смещен в сторону относительно падающего луча АВ. Величина смещения h=EC зависит от толщины пластинки и углов падения и преломления. Смещение, очевидно, тем меньше, чем тоньше пластинка.
Расстояние, на которое смещает пластинка лучи света можно найти по формуле: , (1.6)
или, так как ι<900 и i1<900, i=i1, откуда следует, что лучи АВ и CD параллельны.
Луч CD смещен в сторону относительно падающего луча АВ. Величина смещения h=EC зависит от толщины пластинки и углов падения и преломления. Смещение, очевидно, тем меньше, чем тоньше пластинка.
Расстояние, на которое смещает пластинка лучи света можно найти по формуле:
| |
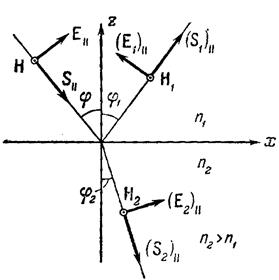 Рис. 9.1.Направления векторов
Рис. 9.1.Направления векторов  и и 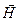 на границе раздела.
Вектор на границе раздела.
Вектор  лежит в плоскости падения.
Направление векторов лежит в плоскости падения.
Направление векторов 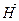 , , 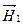 и и 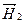 определяется выбором направления для определяется выбором направления для 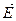 , , 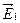 и и 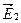 . В данном случае векторы . В данном случае векторы 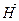 , , 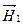 и и 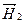 направлены одинаково — перпендикулярно к плоскости чертежа по направлению к читателю. Для проекций амплитуд векторов направлены одинаково — перпендикулярно к плоскости чертежа по направлению к читателю. Для проекций амплитуд векторов 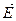 и и 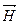 имеем: имеем:
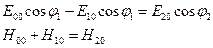 .
Учитывая, что .
Учитывая, что 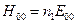 , , 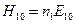 , , 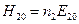 , а также , а также 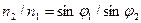 , находим: , находим:
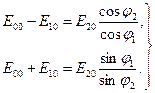 (9.1)
Тогда (9.1)
Тогда
| |  , (1.7)
где d – толщина пластинки.
1.3. Преломление света в призме.
Пусть луч АВ падает на одну из граней призмы (рис.1.3), преломившись в точке В, луч пойдет по направлению ВС и, вторично преломившись в точке С, выйдет из призмы воздух. Найдем угол D, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим p. Из четырехугольника BQCN в котором углы при В и С – прямые, найдем, что угол BNC равен 1800-p. Пользуясь этим, из четырехугольника BMCN находим: , (1.7)
где d – толщина пластинки.
1.3. Преломление света в призме.
Пусть луч АВ падает на одну из граней призмы (рис.1.3), преломившись в точке В, луч пойдет по направлению ВС и, вторично преломившись в точке С, выйдет из призмы воздух. Найдем угол D, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим p. Из четырехугольника BQCN в котором углы при В и С – прямые, найдем, что угол BNC равен 1800-p. Пользуясь этим, из четырехугольника BMCN находим:
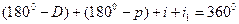 , (1.8)
отсюда: , (1.8)
отсюда:
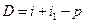 . (1.9)
Угол p, как внешний угол в треугольнике BCN, равен: . (1.9)
Угол p, как внешний угол в треугольнике BCN, равен:
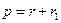 , (1.10) , (1.10)
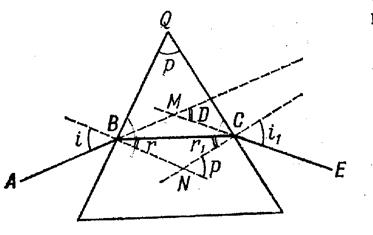 Рис. 1.3.
Рис. 1.3.
| |
|

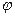 должен наблюдаться выраженный минимум коэффициента отражения, т. е. интенсивность света должна быть минимальной. Данное значение угла поворота и есть угол Брюстера.
4. Вычислите по формуле
должен наблюдаться выраженный минимум коэффициента отражения, т. е. интенсивность света должна быть минимальной. Данное значение угла поворота и есть угол Брюстера.
4. Вычислите по формуле 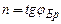 коэффициент преломления исследуемого объекта.
5. Повторите опыт еще 4 раза при других положениях модулей 12 и 13.
6. Выполните аналогичные измерения, заменив объект 4 объектом 5.
7. Результаты для каждого объекта поместите в отдельной таблице:
коэффициент преломления исследуемого объекта.
5. Повторите опыт еще 4 раза при других положениях модулей 12 и 13.
6. Выполните аналогичные измерения, заменив объект 4 объектом 5.
7. Результаты для каждого объекта поместите в отдельной таблице:
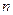
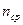
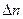
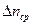
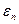 , %
, % 
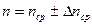 ,
, 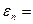 …%
…% Рис. 12.
Модуль 13 (стол поворотный, рис.12) предназначен для установки объектов с возможностью поворота вокруг вертикальной оси, а также для отсчета угловых координат и углов поворота. Поворот стола производится ручкой 1. Отсчет угловых координат производится по основной шкале 2 (цена деления 20) и нониусу 3 (цена деления 0,50). Рычаг 4 поворачивают до совпадения его вертикальной риски с одним из делений основной шкалы и снимают отсчет по основной шкале. К полученному значению прибавляют отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10, при погрешности порядка 0,20. углы поворота определяют как разности угловых координат. Объекты вставляют в кронштейны 5; винтом 6 регулируют наклон платформы стола и установленного на столе объекта.
Набор объектов
При выполнении лабораторных работ помимо функциональных модулей используется также ряд объектов. Большая часть объектов – тонкие пластины, пленки или линзы, расположенные в средней плоскости соответствующего экрана. При установке экрана в кассету функционального модуля эта плоскость оказывается напротив риски рейтера или иной характерной отметки на модуле. Тем самым определяется координата объекта на оптической скамье.
Рис. 12.
Модуль 13 (стол поворотный, рис.12) предназначен для установки объектов с возможностью поворота вокруг вертикальной оси, а также для отсчета угловых координат и углов поворота. Поворот стола производится ручкой 1. Отсчет угловых координат производится по основной шкале 2 (цена деления 20) и нониусу 3 (цена деления 0,50). Рычаг 4 поворачивают до совпадения его вертикальной риски с одним из делений основной шкалы и снимают отсчет по основной шкале. К полученному значению прибавляют отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10, при погрешности порядка 0,20. углы поворота определяют как разности угловых координат. Объекты вставляют в кронштейны 5; винтом 6 регулируют наклон платформы стола и установленного на столе объекта.
Набор объектов
При выполнении лабораторных работ помимо функциональных модулей используется также ряд объектов. Большая часть объектов – тонкие пластины, пленки или линзы, расположенные в средней плоскости соответствующего экрана. При установке экрана в кассету функционального модуля эта плоскость оказывается напротив риски рейтера или иной характерной отметки на модуле. Тем самым определяется координата объекта на оптической скамье.
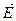 не параллельны плоскости падения (горизонтальная плоскость), т. к. поляризатор неидеальный. Найденный угол и будет являться углом Брюстера.
Эксперимент
1. Установка оборудования.
Для проведения работы, необходимо установить на оптической скамье модуль 12, представляющий собой поляризатор с нониусом, модуль 13 – стол поворотный, в который установлена плоскопараллельная пластинка (объект 4)) последовательно друг за другом.
2. Калибровка установки.
После установки приборов необходимо произвести калибровку установки. Сначала при помощи ручки 1 (рис. ) поворотного стола устанавливают его на нулевую угловую координату, рычаг 4 поворачивают до совпадения его вертикальной риски с нулевым делением основной шкалы.
Затем двумя передними винтами 6 и двумя задними винтами 2 излучателя (рис. ) добиваются совпадение падающего и отраженного света (отраженный свет должен попасть в трубку излучателя).
Так определяется положение нормали к пластинке.
3. Измерения.
Задание 1.
1. Добейтесь максимальной поляризации света в горизонтальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в горизонтальное положение так, чтобы нулевая координата оси поляризатора была напротив риски нониуса.
не параллельны плоскости падения (горизонтальная плоскость), т. к. поляризатор неидеальный. Найденный угол и будет являться углом Брюстера.
Эксперимент
1. Установка оборудования.
Для проведения работы, необходимо установить на оптической скамье модуль 12, представляющий собой поляризатор с нониусом, модуль 13 – стол поворотный, в который установлена плоскопараллельная пластинка (объект 4)) последовательно друг за другом.
2. Калибровка установки.
После установки приборов необходимо произвести калибровку установки. Сначала при помощи ручки 1 (рис. ) поворотного стола устанавливают его на нулевую угловую координату, рычаг 4 поворачивают до совпадения его вертикальной риски с нулевым делением основной шкалы.
Затем двумя передними винтами 6 и двумя задними винтами 2 излучателя (рис. ) добиваются совпадение падающего и отраженного света (отраженный свет должен попасть в трубку излучателя).
Так определяется положение нормали к пластинке.
3. Измерения.
Задание 1.
1. Добейтесь максимальной поляризации света в горизонтальной плоскости. Для этого установите рукоятку 4 излучателя и рукоятку поляризатора в горизонтальное положение так, чтобы нулевая координата оси поляризатора была напротив риски нониуса.
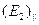 . Вместе с тем
. Вместе с тем 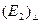 будет раскачивать электроны в направлении, перпендикулярном к плоскости падения, и такое излучение будет распространяться без всяких ограничений в направлении, удовлетворяющей условию (9.5), целиком определяя поляризацию отраженной волны.
Порядок выполнения работы
Для экспериментального определения угла Брюстера пользуются тем, что при некотором значении угла падения от границы раздела двух диэлектриков отразится только электромагнитная волна с такой поляризацией, в которой колебания вектора
будет раскачивать электроны в направлении, перпендикулярном к плоскости падения, и такое излучение будет распространяться без всяких ограничений в направлении, удовлетворяющей условию (9.5), целиком определяя поляризацию отраженной волны.
Порядок выполнения работы
Для экспериментального определения угла Брюстера пользуются тем, что при некотором значении угла падения от границы раздела двух диэлектриков отразится только электромагнитная волна с такой поляризацией, в которой колебания вектора 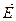 параллельны плоскости падения. В нашем эксперименте это горизонтальная плоскость, т. е. нужно добиться чтобы вектор
параллельны плоскости падения. В нашем эксперименте это горизонтальная плоскость, т. е. нужно добиться чтобы вектор  Рис. 9.6. Схема установки. Колебания вектора
Рис. 9.6. Схема установки. Колебания вектора 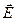 в плоскости падения условно обозначены стрелками, колебания, перпендикулярные плоскости пдания – точками.
в плоскости падения условно обозначены стрелками, колебания, перпендикулярные плоскости пдания – точками.
 Рис. 9.4. Нормали к преломленной и ораженным волнам при падении света
на границу раздела двух сред под углом Брюстера перпендикулярны.
Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном к нормали к преломленной волне, не должна распространяться энергия, так как электрон не излучает в направлении, вдоль которого происходят его колебания (рис. 9.5).
Рис. 9.4. Нормали к преломленной и ораженным волнам при падении света
на границу раздела двух сред под углом Брюстера перпендикулярны.
Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном к нормали к преломленной волне, не должна распространяться энергия, так как электрон не излучает в направлении, вдоль которого происходят его колебания (рис. 9.5).
 Рис. 9.5. К трактовке закона Брюстера с позиций электронной теории.
Вектор
Рис. 9.5. К трактовке закона Брюстера с позиций электронной теории.
Вектор 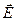 в падающей волне лежит в плоскости падения. Отраженная волна этой gоляризации отсутствует, т.к. электроны не излучают в направлении своих колебаний.
Легко заметить, что последнее ограничение относится лишь к колебаниям электронов в плоскости падения волны, происходящим в
в падающей волне лежит в плоскости падения. Отраженная волна этой gоляризации отсутствует, т.к. электроны не излучают в направлении своих колебаний.
Легко заметить, что последнее ограничение относится лишь к колебаниям электронов в плоскости падения волны, происходящим в  Рис. 1.1.
Доказательством прямолинейности распространения света служит образование тени. От точечного источника света возникает полная тень. Лучи, исходящие из одной точки, образуют расходящийся пучок (сечение пучка увеличивается). Лучи, сходящиеся в одну точку, образуют сходящийся пучок.
Рис. 1.1.
Доказательством прямолинейности распространения света служит образование тени. От точечного источника света возникает полная тень. Лучи, исходящие из одной точки, образуют расходящийся пучок (сечение пучка увеличивается). Лучи, сходящиеся в одну точку, образуют сходящийся пучок.
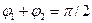 , то
, то 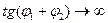 и, следовательно,
и, следовательно, 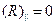 . Вместе с тем коэффициент отражения
. Вместе с тем коэффициент отражения 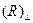 не обращается в нуль при
не обращается в нуль при 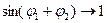 . Таким образом, получается, что при некотором значении угла падения от границы раздела отразится только электромагнитная волна с вполне определенной поляризацией. Волна, в которой колебания вектора
. Таким образом, получается, что при некотором значении угла падения от границы раздела отразится только электромагнитная волна с вполне определенной поляризацией. Волна, в которой колебания вектора 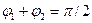 . Вектор
. Вектор 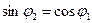 и, значит,
и, значит,
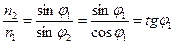 .
Эта зависимость угла, при котором наблюдается плоская поляризация отраженной волны, от отношения показателей преломления двух исследуемых диэлектриков носит название закона Брюстера, а соответствующий угол часто называют углом Брюстера
.
Эта зависимость угла, при котором наблюдается плоская поляризация отраженной волны, от отношения показателей преломления двух исследуемых диэлектриков носит название закона Брюстера, а соответствующий угол часто называют углом Брюстера  . В этих обозначениях
. В этих обозначениях
 . (9.5)
Для перехода световой волны (видимая область спектра) из воздуха в стекло
. (9.5)
Для перехода световой волны (видимая область спектра) из воздуха в стекло  , что соответствует углу
, что соответствует углу 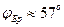 .
.
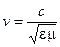 , где c= 3·108 м/с – скорость света в вакууме, ε – относительная диэлектрическая проницаемость среды, μ – относительная магнитная проницаемость среды (для подавляющего большинства диэлектрических сред
, где c= 3·108 м/с – скорость света в вакууме, ε – относительная диэлектрическая проницаемость среды, μ – относительная магнитная проницаемость среды (для подавляющего большинства диэлектрических сред 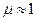 ). Отношение
). Отношение
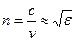 (1.1)
называется абсолютным показателем преломления света. Отношение
(1.1)
называется абсолютным показателем преломления света. Отношение
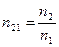 (1.2)
называется относительным показателем преломления света средой 2 по отношению к среде 1.
Формулы (1.1), (1.2) справедливы только для волн, частоты которых малы по сравнению с частотой процессов в атомах и молекулах среды. Вследствие дисперсии показателя преломления данные формулы справедливы лишь для монохроматических волн. Среды, в которых распространяются отраженная и преломленная волны, считаются полубесконечными, т.е. принимается, что на границе раздела сходятся только три волны: падающая, отраженная, преломленная, т.е. пренебрегают многократным отражением.
При падении световой волны на идеальную плоскую границу раздела 2-х диэлектриков, размеры которой значительно превышают длину волны, угол между направлением распространения отраженной волны и нормалью к границе раздела ι’1 (угол отражения) равен по абсолютной величине соответствующему углу для падающей волны ι1 (закон отражения, рис.1.1). Угол между направлением распространения преломленной волны и нормалью к границе раздела (угол преломления ι2) связан с углом падения законом преломления света:
(1.2)
называется относительным показателем преломления света средой 2 по отношению к среде 1.
Формулы (1.1), (1.2) справедливы только для волн, частоты которых малы по сравнению с частотой процессов в атомах и молекулах среды. Вследствие дисперсии показателя преломления данные формулы справедливы лишь для монохроматических волн. Среды, в которых распространяются отраженная и преломленная волны, считаются полубесконечными, т.е. принимается, что на границе раздела сходятся только три волны: падающая, отраженная, преломленная, т.е. пренебрегают многократным отражением.
При падении световой волны на идеальную плоскую границу раздела 2-х диэлектриков, размеры которой значительно превышают длину волны, угол между направлением распространения отраженной волны и нормалью к границе раздела ι’1 (угол отражения) равен по абсолютной величине соответствующему углу для падающей волны ι1 (закон отражения, рис.1.1). Угол между направлением распространения преломленной волны и нормалью к границе раздела (угол преломления ι2) связан с углом падения законом преломления света:
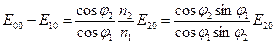 .
Отсюда легко получаются искомые зависимости
.
Отсюда легко получаются искомые зависимости
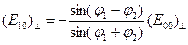 ,
, 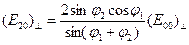 . (9.4)
Займемся анализом найденных соотношений. Прежде всего рассмотрим относительные интенсивности отраженной и преломленной волн. Проанализируем зависимость коэффициента отражения
. (9.4)
Займемся анализом найденных соотношений. Прежде всего рассмотрим относительные интенсивности отраженной и преломленной волн. Проанализируем зависимость коэффициента отражения 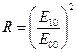 от угла падения (рис 9.3).
от угла падения (рис 9.3).
 Рис.9.3. Зависимость коэффициента отражения R от угла падения
При переходе света из воздуха (n1»1) в стекло (n2»1,5).
Рассмотрение формул Френеля показывает, что компоненты
Рис.9.3. Зависимость коэффициента отражения R от угла падения
При переходе света из воздуха (n1»1) в стекло (n2»1,5).
Рассмотрение формул Френеля показывает, что компоненты 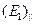 , и
, и 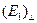 , по-разному изменяются с увеличением угла
, по-разному изменяются с увеличением угла 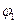 . Во-пер
. Во-пер 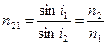 (1.3)
где n21 – относительный показатель преломления среды, в которой распространяется свет, относительно среды в которой распространяется падающий свет.
Если световая волна из оптически более плотной среды 1 падает на границу раздела с оптически менее плотной средой 2 (т.е. если
(1.3)
где n21 – относительный показатель преломления среды, в которой распространяется свет, относительно среды в которой распространяется падающий свет.
Если световая волна из оптически более плотной среды 1 падает на границу раздела с оптически менее плотной средой 2 (т.е. если 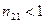 ), то при угле падения i1>iкр где siniкр=n21, величина sini2>1, что невозможно. Угол iкр при котором i2=900 и преломленная волна отсутствует, называется критическим углом падения света. Явления отражения света целиком в первую среду называется полным внутренним отражением света. Энергия падающей электромагнитной волны полностью возвращается в первую среду, но места захода падающей и выхода отраженной волны на границе раздела смещены друг относительно друга на расстояние порядка половины длины световой волны.
Отношение интенсивности отраженной волны к интенсивности падающей называется коэффициентом отражения света второй среды относительно первой. Отношение интенсивностей преломленной к интенсивности падающей волны называется коэффициентом пропускания второй среды относительно первой.
), то при угле падения i1>iкр где siniкр=n21, величина sini2>1, что невозможно. Угол iкр при котором i2=900 и преломленная волна отсутствует, называется критическим углом падения света. Явления отражения света целиком в первую среду называется полным внутренним отражением света. Энергия падающей электромагнитной волны полностью возвращается в первую среду, но места захода падающей и выхода отраженной волны на границе раздела смещены друг относительно друга на расстояние порядка половины длины световой волны.
Отношение интенсивности отраженной волны к интенсивности падающей называется коэффициентом отражения света второй среды относительно первой. Отношение интенсивностей преломленной к интенсивности падающей волны называется коэффициентом пропускания второй среды относительно первой.
 Рис. 1.2.
В геометрической оптике каждая точка источника света считается центром расходящегося
Рис. 1.2.
В геометрической оптике каждая точка источника света считается центром расходящегося
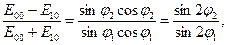
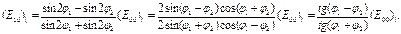 (9.2)
Складывая уравнения (2.1), получаем:
(9.2)
Складывая уравнения (2.1), получаем:
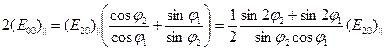 ,
откуда
,
откуда
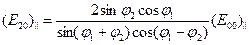 . (9.3)
2. Вектор
. (9.3)
2. Вектор 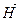 ,
,  и
и 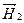 согласно рис. 9.2. На нем векторы
согласно рис. 9.2. На нем векторы 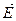 ,
, 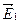 и
и 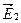 направлены от читателя перпендикулярно к плоскости чертежа.
направлены от читателя перпендикулярно к плоскости чертежа.
 Рис. 9.2. Направления векторов
Рис. 9.2. Направления векторов 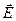 и
и 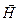 на границе раздела.
Вектор
на границе раздела.
Вектор 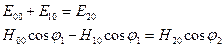
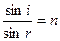 , (1.4)
где n – показатель преломления пластинки. Для преломления в точке С закон (1.3) дает:
, (1.4)
где n – показатель преломления пластинки. Для преломления в точке С закон (1.3) дает:
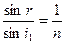 , (1.5)
так как в этом случае луч выходит из пластинки в воздух. Перемножив выражения (1.4) и (1.5), находим:
, (1.5)
так как в этом случае луч выходит из пластинки в воздух. Перемножив выражения (1.4) и (1.5), находим:
 , (1.6)
или, так как ι<900 и i1<900, i=i1, откуда следует, что лучи АВ и CD параллельны.
Луч CD смещен в сторону относительно падающего луча АВ. Величина смещения h=EC зависит от толщины пластинки и углов падения и преломления. Смещение, очевидно, тем меньше, чем тоньше пластинка.
Расстояние, на которое смещает пластинка лучи света можно найти по формуле:
, (1.6)
или, так как ι<900 и i1<900, i=i1, откуда следует, что лучи АВ и CD параллельны.
Луч CD смещен в сторону относительно падающего луча АВ. Величина смещения h=EC зависит от толщины пластинки и углов падения и преломления. Смещение, очевидно, тем меньше, чем тоньше пластинка.
Расстояние, на которое смещает пластинка лучи света можно найти по формуле:
 Рис. 9.1.Направления векторов
Рис. 9.1.Направления векторов  и
и 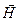 на границе раздела.
Вектор
на границе раздела.
Вектор 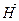 ,
, 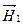 и
и 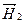 определяется выбором направления для
определяется выбором направления для 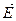 ,
, 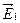 и
и 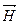 имеем:
имеем:
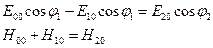 .
Учитывая, что
.
Учитывая, что 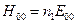 ,
, 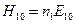 ,
, 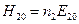 , а также
, а также 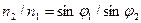 , находим:
, находим:
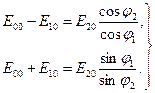 (9.1)
Тогда
(9.1)
Тогда
 , (1.7)
где d – толщина пластинки.
1.3. Преломление света в призме.
Пусть луч АВ падает на одну из граней призмы (рис.1.3), преломившись в точке В, луч пойдет по направлению ВС и, вторично преломившись в точке С, выйдет из призмы воздух. Найдем угол D, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим p. Из четырехугольника BQCN в котором углы при В и С – прямые, найдем, что угол BNC равен 1800-p. Пользуясь этим, из четырехугольника BMCN находим:
, (1.7)
где d – толщина пластинки.
1.3. Преломление света в призме.
Пусть луч АВ падает на одну из граней призмы (рис.1.3), преломившись в точке В, луч пойдет по направлению ВС и, вторично преломившись в точке С, выйдет из призмы воздух. Найдем угол D, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим p. Из четырехугольника BQCN в котором углы при В и С – прямые, найдем, что угол BNC равен 1800-p. Пользуясь этим, из четырехугольника BMCN находим:
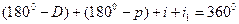 , (1.8)
отсюда:
, (1.8)
отсюда:
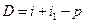 . (1.9)
Угол p, как внешний угол в треугольнике BCN, равен:
. (1.9)
Угол p, как внешний угол в треугольнике BCN, равен:
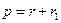 , (1.10)
, (1.10)
 Рис. 1.3.
Рис. 1.3.