Задание 2. Дифракция Фраунгофера на одномерной дифракционной решетке 1 страница
При проведении расчета предполагается наличие определенных соотношений между электрическими моментами, вызываемыми плоской волной в разных участках (радикалах) изучаемой сложной молекулы, и учитывается изменение фазы волны в её пределах.
В результате расчета находим
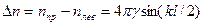 ,
где ,
где 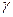 - некоторая константа, а - некоторая константа, а 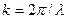 - волновое число. Нетрудно заметить, что при l=0 имеем - волновое число. Нетрудно заметить, что при l=0 имеем 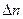 =0, и плоскость поляризации не вращается. =0, и плоскость поляризации не вращается.
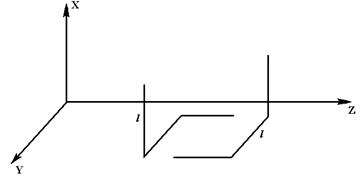 Рис. 10.6.
Рис. 10.6.
| | ФЕДЕРАЦИИ ПО РЫБОЛОВСТВУ
АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ФИЗИКИ
ФИЗИЧЕСКИЙ ПРАКТИКУМ
ОПТИКА
учебно-методическое
пособие
 АСТРАХАНЬ – 2003
АСТРАХАНЬ – 2003
| |
В случае кристаллов главной причиной различия скоростей следует считать асимметрию внешней формы (отсутствие центра симметрии) — об этом говорит уже упоминавшаяся выше возможность различать кристалл правого и левого кварца по внешнему виду. Для аморфных однородных тел нужно связать исследуемое явление со строением сложных молекул активной среды.
Этот вопрос был подробно рассмотрен М. Борном (1915 г.), который показал, что описанный выше эффект можно объяснить, если учесть взаимодействие электромагнитного поля с веществом в пределах одной молекулы. При построении теории принималось во внимание, что все оптически активные вещества существуют в двух модификациях, характеризующихся правым и левым вращением плоскости поляризации, и рассматривались сложные асимметричные молекулы с пространственной структурой, не имеющие ни центра симметрии, ни плоскости симметрии. Наиболее простая модель такой молекулы — отрезок спирали.
Пусть на такую молекулу, диаметр витка которой равен a, падает плоско поляризованная волна Е = Ех (рис.10.5). Она вызовет движение зарядов, направленное вдоль оси х. Но если заряды будут двигаться вдоль спирали, то неизбежно возникнет их движение и вдоль оси у. Следовательно, можно говорить об y- компоненте волны в веществе, наличие которой должно привести к отклонению плоскости колебаний от направления Е = Еx. Расчет должен быть связан с изменением фазы волны в пределах одной молекулы (вместо ωt нужно взять ωt-ka), а его результат покажет, будет ли такое изменение существенно. На первый взгляд этот эффект кажется пренебрежимо малым, так как для оптической области отношение размера молекулы к длине волны порядка 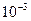 , но возможность выявления в эксперименте чрезвычайно малых , но возможность выявления в эксперименте чрезвычайно малых 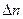 не позволяет заранее отвергнуть подобное предложение.
Так, например, для модели асимметричной молекулы, изображенной на рис.10.6. будет иметь место поворот плоскости поляризации волны, распространяющейся вдоль оси z, причем величина не позволяет заранее отвергнуть подобное предложение.
Так, например, для модели асимметричной молекулы, изображенной на рис.10.6. будет иметь место поворот плоскости поляризации волны, распространяющейся вдоль оси z, причем величина 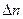 оказывается зависящей от размера молекулы l. оказывается зависящей от размера молекулы l.
| | | Учебно-методическое пособие для студентов инженерно-технических специальностей всех форм обучения. Включает описания деяти лабораторных работ по волновой оптике (разделы «геометрическая оптика», «фотометрия», «интерференция света», «дифракция света», «поляризация света»), выполняемых на лабораторном оптическом комплексе ЛКО-3П фирмы ВЛАДОС (г. Москва).
Авторы:
к.ф.м.н Карибьянц В.Р. (введение, работы №№ 1 – 10),
Кузьмин С.И. (работы №№ 1 – 7),
Чешев В.Г. (работы №№ 1 – 7),
Ковалев С. (работа № 8),
Филин (работа № 9),
Им И. (работа № 10)
Под редакцией к.ф.м.н. В.Р.Карибьянца.
Рецензенты: к.ф.м.н., доц. В.И.Евдашкин, к.ф.м.н. В.Ю.Маньков.
Учебно- методическое пособие рассмотрено и утверждено к печати на заседании кафедры физики АГТУ
(протокол № от 2003).
| |
Здесь множители, выделенные снизу фигурной скобкой, являются проекциями на оси х и у амплитуд суммарного колебания.
Рассмотрение (10.2) и (10.3) показывает, что фазы колебаний 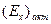 и и 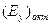 одинаковы. Следовательно, между колебанием вдоль оси х и колебанием вдоль оси у нет сдвига фаз одинаковы. Следовательно, между колебанием вдоль оси х и колебанием вдоль оси у нет сдвига фаз 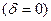 , и в результате сложения этих колебаний получится плоско поляризованная волна. В результате прохождения в активной среде пути z = d плоскость поляризации повернется на угол φ. Из сравнения проекций амплитуды , и в результате сложения этих колебаний получится плоско поляризованная волна. В результате прохождения в активной среде пути z = d плоскость поляризации повернется на угол φ. Из сравнения проекций амплитуды 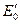 на оси у и х определяем значение угла φ : на оси у и х определяем значение угла φ :
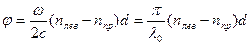 (10.4)
Итак можно считать, что в рамках феноменологической электромагнитной теории света вращение плоскости поляризации получило объяснение. Однако (10.4)
Итак можно считать, что в рамках феноменологической электромагнитной теории света вращение плоскости поляризации получило объяснение. Однако
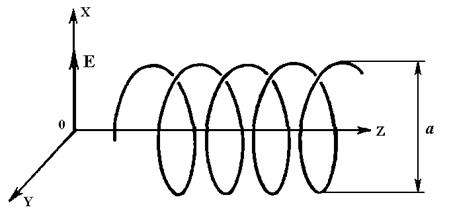 Рис. 10.5.
эта теория не способна объяснить, почему скорость волны в правовращающем веществе отлична от ее скорости в левовращающем (
Рис. 10.5.
эта теория не способна объяснить, почему скорость волны в правовращающем веществе отлична от ее скорости в левовращающем ( 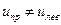 ). Если попытаться ответить на этот вопрос с позиций молекулярной теории, то нужно предположить, что вращение плоскости поляризации связано, с асимметрией строения оптически активного вещества. ). Если попытаться ответить на этот вопрос с позиций молекулярной теории, то нужно предположить, что вращение плоскости поляризации связано, с асимметрией строения оптически активного вещества. | | Введение
В настоящее учебно-методическое пособие включены описания десяти лабораторных работ по геометрической и волновой оптике, выполняющихся на базе лабораторного комплекса ЛКО-3П фирмы «Владос» (г. Москва).
Пособие составлено в соответствии с рабочими программами по физике для инженерно-технических специальностей и может быть использовано при работе со студентами всех форм обучения. Каждая лабораторная работа помимо подробного описания учебного эксперимента содержит краткое изложение соответствующей теории. При отборе теоретического материала авторы стремились по возможности избежать излишнего дублирования распространенных учебников и сложившихся лекционных курсов: большее внимание уделено вопросам, включенным в программу, но традиционно слабо освещаемым на лекциях (например, вывод формул Френеля, физический механизм вращения плоскости поляризации света и др.). Описания всех работ снабжены контрольными вопросами и списком дополнительной литературы.
Рекомендуемое аудиторное время на выполнение и отчет по каждой лабораторной работе – 4 академических часа. В течение учебного семестра студентам специальностей, учебными планами по физике которых предусмотрено 16 или 18 часов лабораторных работ, рекомендуется выполнить 4 работы: №№ 1, 4, 6 и 8. Студентам специальностей, предусматривающих 34 или 36 аудиторных часов лабораторных работ, рекомендуется выполнить 7 работ, из которых 4 перечислены выше, а еще 3 либо назначаются ведущим преподавателем, либо выбираются по усмотрению самих студентов.
При написании пособия была использована следующая литература:
- Описание работ фирмы «Владос».
- И.В.Савельев. Курс общей физики. Том 2. М.: Наука, 1978, 480 с.
- Ландсберг. Оптика.
- Волновая физика.
- Т.И.Трофимова. Курс физики. М.: Высшая школа, 1998, 542 с.
- Б.М.Яворский, А.А.Пинский. Основы физики. Том 2. М.: Наука, 1974, 464 с.
- Н.Н.Майсова. Практикум по курсу общей физики. М.: Высшая школа, 1970, 448 с.
| |
Правое вращение: Левое вращение:
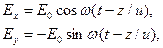 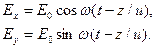 (10.1) (10.1)  Отсюда вытекает законность разложения плоско поляризованного колебания на два колебания поляризованных по кругу с правым и левым вращением. Для неактивного вещества
Отсюда вытекает законность разложения плоско поляризованного колебания на два колебания поляризованных по кругу с правым и левым вращением. Для неактивного вещества 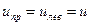 , и если, например, , и если, например, 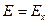 , то обе равные по величине и противоположные по знаку y-компоненты в сумме дадут нуль.
Теперь учтем сделанное выше предположение, что в активном веществе , то обе равные по величине и противоположные по знаку y-компоненты в сумме дадут нуль.
Теперь учтем сделанное выше предположение, что в активном веществе 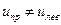 . Запишем теперь выражение для волны, распространяющейся в активном веществе: x- компонента напряженности электрического поля . Запишем теперь выражение для волны, распространяющейся в активном веществе: x- компонента напряженности электрического поля 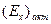 равна сумме равна сумме 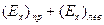 , а y- компонента , а y- компонента 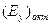 - сумме - сумме 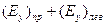 . Вместо . Вместо 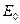 в(10.1) нужно ввести другую амплитуду в(10.1) нужно ввести другую амплитуду 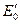 , меньшую , меньшую 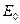 , так как часть энергии отразилась при входе в среду.
Итак, x- компонента волны в оптически активной среде запишется в виде: , так как часть энергии отразилась при входе в среду.
Итак, x- компонента волны в оптически активной среде запишется в виде:
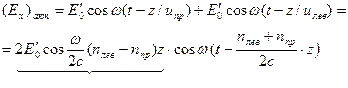 (10.2)
Аналогично для y- компоненты имеем (10.2)
Аналогично для y- компоненты имеем
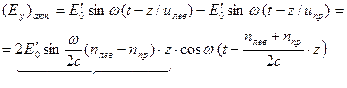 (10.3) (10.3)
| |
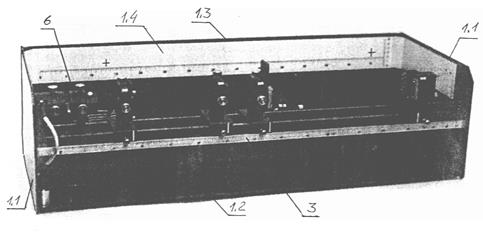 Рис.1. Общий вид лабораторной установки ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П предназначен для постановки лабораторных работ по оптике в физическом практикуме вузов. Позволяет изучать закономерности геометрической оптики, интерференции, дифракции, поляризации, а также их применение к решению измерительных задач.
Общий вид установки ЛКО-3П приведен на рис.1. Каркас установки состоит из двух боковин 1.1, стянутых оптической скамьей 3, плитой-основанием 1.2 и задней стенкой 1.3. В задней части каркаса размещена кассета с объектами. Вдоль каркаса размещена оптическая скамья 3, состоящая из двух рельс со шкалой (линейкой) с ценой деления 2 мм. Оптическая ось установки расположена симметрично относительно оптической скамьи на высоте 45 мм от верхнего края рельс.
Излучатель 6 (лазер в держателе с 5 степенями свободы) установлен на оптической оси установки над оптической скамьей. С помощью отражателя микропроектора исследуемое излучение направляется на экран, расположенный на задней стенке каркаса.
Рис.1. Общий вид лабораторной установки ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П предназначен для постановки лабораторных работ по оптике в физическом практикуме вузов. Позволяет изучать закономерности геометрической оптики, интерференции, дифракции, поляризации, а также их применение к решению измерительных задач.
Общий вид установки ЛКО-3П приведен на рис.1. Каркас установки состоит из двух боковин 1.1, стянутых оптической скамьей 3, плитой-основанием 1.2 и задней стенкой 1.3. В задней части каркаса размещена кассета с объектами. Вдоль каркаса размещена оптическая скамья 3, состоящая из двух рельс со шкалой (линейкой) с ценой деления 2 мм. Оптическая ось установки расположена симметрично относительно оптической скамьи на высоте 45 мм от верхнего края рельс.
Излучатель 6 (лазер в держателе с 5 степенями свободы) установлен на оптической оси установки над оптической скамьей. С помощью отражателя микропроектора исследуемое излучение направляется на экран, расположенный на задней стенке каркаса.
| |
Для того чтобы результирующее колебание осталось плоско поляризованным, неизбежно должна повернуться плоскость симметрии. Для определения направления колебаний в результирующей плоско поляризованной волне нужно сложить две поляризованные по кругу волны после прохождения ими равного пути в оптически активной среде, то есть найти плоскость симметрии, которая (см. рис. 10.4) должна разделить пополам разность углов 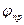 и и 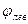 . Отсюда ясно, что плоскость колебаний вектора Е в результирующей плоско поляризованной волне повернется по отношению к направлению колебаний в исходной волне на угол . Отсюда ясно, что плоскость колебаний вектора Е в результирующей плоско поляризованной волне повернется по отношению к направлению колебаний в исходной волне на угол
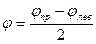 Нетрудно получить основные соотношения для угла поворота плоскости поляризации в привычных обозначениях электромагнитной теории. Если плоско поляризованная волна описывалась выражением
Нетрудно получить основные соотношения для угла поворота плоскости поляризации в привычных обозначениях электромагнитной теории. Если плоско поляризованная волна описывалась выражением
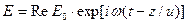 ,
то аналитическое выражение для волны, поляризованной по кругу, нужно записать в виде ,
то аналитическое выражение для волны, поляризованной по кругу, нужно записать в виде
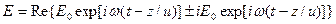 .
Это ясно из того, что круговое колебание всегда можно получить сложением двух взаимно перпендикулярных колебаний равной амплитуды с разностью фаз .
Это ясно из того, что круговое колебание всегда можно получить сложением двух взаимно перпендикулярных колебаний равной амплитуды с разностью фаз 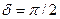 . Так как . Так как 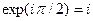 , то появление разности фаз , то появление разности фаз 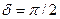 между компонентами Ех и Еу эквивалентно умножению одной из них на i, а знак ± соответствует правому или левому вращению.
При определении знака вращения следует иметь в виду, что при правом вращении компонента Еу опережает Ех на между компонентами Ех и Еу эквивалентно умножению одной из них на i, а знак ± соответствует правому или левому вращению.
При определении знака вращения следует иметь в виду, что при правом вращении компонента Еу опережает Ех на 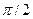 , т.е. , т.е. 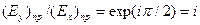 , а при левом вращении Еу отстает от Ех на , а при левом вращении Еу отстает от Ех на 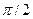 т. е. т. е. 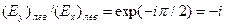 . Следовательно (учитывая, что . Следовательно (учитывая, что 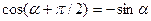 ), имеем: ), имеем:
| | На задней стенке каркаса размещен экран 1.4. Он содержит шкалу длиной 73 см с ценой деления 1мм. Ноль шкалы экрана расположен напротив ноля линейки оптической скамьи (смещение не более 1 мм). Над шкалой изображены два визирных креста с координатами 13,0 и 70,0 см, используемые при настройке установки. Центры крестов находятся на уровне оптической оси установки.
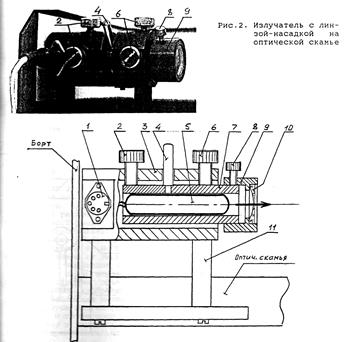 Схема излучателя приведена на рис.2. Лазер, смонтированный со схемой стабилизации тока в оправе 5, вставлен в трубу 7, закрепленную подвижно в корпусе 3. Корпус установлен на двух стойках 11. Двумя передними винтами 6 и двумя задними винтами 2 лазер можно перемещать относительно корпуса, подбирая нужное положение и направление пучка излучения. Поляризация излучения – линейная. Плоскость колебаний вектора Е параллельна оси рукоятки 4, с помощью которой лазер поворачивается вокруг оптической оси. Насадка 9 с рассеивающей линзой 10 (объект 42) позволяет получить расходящийся пучок излучения. Насадка крепится на трубе излучателя винтом 8. Питание подается через разъем 1.
Схема излучателя приведена на рис.2. Лазер, смонтированный со схемой стабилизации тока в оправе 5, вставлен в трубу 7, закрепленную подвижно в корпусе 3. Корпус установлен на двух стойках 11. Двумя передними винтами 6 и двумя задними винтами 2 лазер можно перемещать относительно корпуса, подбирая нужное положение и направление пучка излучения. Поляризация излучения – линейная. Плоскость колебаний вектора Е параллельна оси рукоятки 4, с помощью которой лазер поворачивается вокруг оптической оси. Насадка 9 с рассеивающей линзой 10 (объект 42) позволяет получить расходящийся пучок излучения. Насадка крепится на трубе излучателя винтом 8. Питание подается через разъем 1.
| |
(«левого» и «правого») равна удвоенной проекции любого из них на диаметр, т. е. вектору, направление которого постоянно, а величина изменяется по периодическому закону с частотой w. Это и есть плоско поляризованное колебание. Френель предположил, что в оптически активном веществе скорость распространения волны с правым вращением отлична от скорости распространения для волны с левым вращением, т. е. 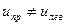 . В силу этого все оптически активные вещества можно подразделить на «правые» ( . В силу этого все оптически активные вещества можно подразделить на «правые» ( 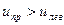 ) и «левые» ( ) и «левые» ( 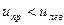 ). ).
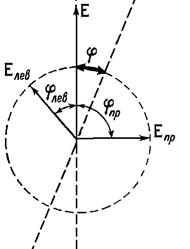 Рис. 10.4.
Рассмотрим, что произойдет с плоско поляризованной волной, распространяющейся в оптически активной среде. Разложим исходную волну Е на две волны, поляризованные по правому и левому кругу, скорости распространения которых в данном веществе не равны. Очевидно, что время, необходимое каждой волне для прохождения одного и того же отрезка в исследуемой активной среде, окажется различным. Следовательно, векторы Епр и Елев повернутся на различные углы
Рис. 10.4.
Рассмотрим, что произойдет с плоско поляризованной волной, распространяющейся в оптически активной среде. Разложим исходную волну Е на две волны, поляризованные по правому и левому кругу, скорости распространения которых в данном веществе не равны. Очевидно, что время, необходимое каждой волне для прохождения одного и того же отрезка в исследуемой активной среде, окажется различным. Следовательно, векторы Епр и Елев повернутся на различные углы 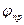 и и 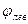 . На рис.10.4, иллюстрирующем эти рассуждения, jпр выбран больше, чем φлев . . На рис.10.4, иллюстрирующем эти рассуждения, jпр выбран больше, чем φлев .
| |
 Рис. 3.
В комплексе ЛКО-3П установлен регулируемый стабилизированный источник тока для лазерного излучателя (рис.3). Разъем питания лазера соединен кабелем с разъемом «ЛАЗЕР» источника тока. К разъему питания «ПИТ» источника тока подключен переносной блок питания.
Ручкой «ТОК» регулируют ток лазера в пределах 20 – 60 мА. Для измерения тока измеряют выведенное на гнезда “U/R” напряжение U на резисторе R=100 Ом, включенном последовательно с лазером. Ток лазера I=U/R.
Функциональные модули
При выполнении лабораторных работ на комплексе ЛКО-3П используются 8 функциональных модулей.
Функциональные модули размещены и установлены на рейтерах (двухкоординатном и поворотном держателях). Рейтеры обеспечивают установку модулей на оптической скамье и перемещение модулей вдоль оптической скамьи. Держатели обеспечивают юстировочные перемещения модулей. Номера модулей нанесены на их корпусах.
Рис. 3.
В комплексе ЛКО-3П установлен регулируемый стабилизированный источник тока для лазерного излучателя (рис.3). Разъем питания лазера соединен кабелем с разъемом «ЛАЗЕР» источника тока. К разъему питания «ПИТ» источника тока подключен переносной блок питания.
Ручкой «ТОК» регулируют ток лазера в пределах 20 – 60 мА. Для измерения тока измеряют выведенное на гнезда “U/R” напряжение U на резисторе R=100 Ом, включенном последовательно с лазером. Ток лазера I=U/R.
Функциональные модули
При выполнении лабораторных работ на комплексе ЛКО-3П используются 8 функциональных модулей.
Функциональные модули размещены и установлены на рейтерах (двухкоординатном и поворотном держателях). Рейтеры обеспечивают установку модулей на оптической скамье и перемещение модулей вдоль оптической скамьи. Держатели обеспечивают юстировочные перемещения модулей. Номера модулей нанесены на их корпусах.
| |
Все оптически активные вещества существуют в дух разновидностях – правовращающей и левовращающей. Существуют право- и левовращающий кварц, право- и левовращающий сахар и т.д. Молекулы и кристаллы одной разновидности являются зеркальным отражением молекул и кристаллов другой разновидности (рис.10.2.).
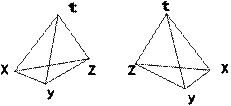 Рис. 10.2.
Рис. 10.2.
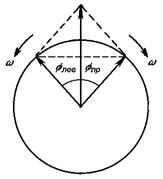 Рис. 10.3.
Эксперименты, подобные описанным выше, легли в основу метода определения концентрации оптически активного вещества путем измерения угла поворота плоскости поляризации. Данный метод имеет многочисленные практические приложения — в частности им пользуются для определения концентрации сахара в производственных растворах и биологических объектах (кровь, моча).
Интерпретация вращения плоскости поляризации была дана впервые Френелем. При изложении сущности формальной теории Френеля прежде всего установим, что любое плоско поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением. Это ясно из геометрического построения, приведенного на рис.10.3. Действительно, сумма двух векторов
Рис. 10.3.
Эксперименты, подобные описанным выше, легли в основу метода определения концентрации оптически активного вещества путем измерения угла поворота плоскости поляризации. Данный метод имеет многочисленные практические приложения — в частности им пользуются для определения концентрации сахара в производственных растворах и биологических объектах (кровь, моча).
Интерпретация вращения плоскости поляризации была дана впервые Френелем. При изложении сущности формальной теории Френеля прежде всего установим, что любое плоско поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением. Это ясно из геометрического построения, приведенного на рис.10.3. Действительно, сумма двух векторов | | 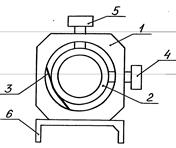 Рис. 4.
Двухкоординатный держатель (рис.4) состоит из корпуса 1 и обоймы 2, удерживаемой пружинами 3 и перемещаемой двумя винтами 4 и 5 в пределах 2 мм от среднего положения по горизонтали и по вертикали. Корпус закреплен на рейтере 6. обойма может поворачиваться на произвольный угол округ горизонтальной оси (оптической оси установки). Такие держатели имеют модули 5,6,8.
Рис. 4.
Двухкоординатный держатель (рис.4) состоит из корпуса 1 и обоймы 2, удерживаемой пружинами 3 и перемещаемой двумя винтами 4 и 5 в пределах 2 мм от среднего положения по горизонтали и по вертикали. Корпус закреплен на рейтере 6. обойма может поворачиваться на произвольный угол округ горизонтальной оси (оптической оси установки). Такие держатели имеют модули 5,6,8.
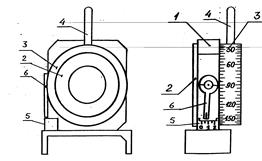 Рис. 5.
Поворотный держатель (рис.5) состоит из корпуса 1 и обоймы 2, соединенной с круговой шкалой 3. Поворот обоймы вокруг оси О-О производится рукояткой 4. Отсчет угловых координат производится по основной шкале 3 (цена деления 20) и нониусу 5 (цена деления 0,50). Рычаг 6 поворачивают до совпадения его горизонтальной риски с одним из делений основной шкалы и снимают отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10 при погрешности
Рис. 5.
Поворотный держатель (рис.5) состоит из корпуса 1 и обоймы 2, соединенной с круговой шкалой 3. Поворот обоймы вокруг оси О-О производится рукояткой 4. Отсчет угловых координат производится по основной шкале 3 (цена деления 20) и нониусу 5 (цена деления 0,50). Рычаг 6 поворачивают до совпадения его горизонтальной риски с одним из делений основной шкалы и снимают отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10 при погрешности | |
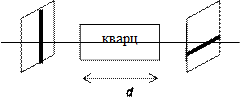 Рис. 10.1.
После введения между поляризатором и анализатором пластинки кварца толщиной d свет начинает проходить через данную оптическую систему. Свет распространяется вдоль оптической оси кварца. Повернув анализатор на угол
Рис. 10.1.
После введения между поляризатором и анализатором пластинки кварца толщиной d свет начинает проходить через данную оптическую систему. Свет распространяется вдоль оптической оси кварца. Повернув анализатор на угол 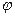 , снова получаем темноту. Опыт даёт , снова получаем темноту. Опыт даёт 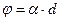 , где d – путь луча, пройденный в кристалле и α - удельная постоянная вращения, причем αсильно зависит от длины волны , где d – путь луча, пройденный в кристалле и α - удельная постоянная вращения, причем αсильно зависит от длины волны 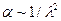 .
В опытах с растворами все выполняется также как и в предыдущем случае, но вместо кварца между поляризаторами вводится кювета с раствором оптически активного вещества. Если обозначить длину кюветы через d, концентрацию вещества через с, то из опыта следует: .
В опытах с растворами все выполняется также как и в предыдущем случае, но вместо кварца между поляризаторами вводится кювета с раствором оптически активного вещества. Если обозначить длину кюветы через d, концентрацию вещества через с, то из опыта следует: 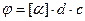 , где [α] - удельная постоянная вращения для данного вещества. Она также сильно зависит от длины волны ( , где [α] - удельная постоянная вращения для данного вещества. Она также сильно зависит от длины волны ( 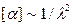 ) и слабо от температуры раствора.
Опыт показывает, что разные модификации одного оптически активного кристаллического вещества (например, разные образцы кварца) вращают плоскость поляризации вправо или влево (если смотреть навстречу световому лучу). Таким образом, различают правое вращение (по часовой стрелке) и левое вращение (против часовой стрелки). Направление вращения луча (относительно луча) не зависит от направления распространения луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл ещё раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации. ) и слабо от температуры раствора.
Опыт показывает, что разные модификации одного оптически активного кристаллического вещества (например, разные образцы кварца) вращают плоскость поляризации вправо или влево (если смотреть навстречу световому лучу). Таким образом, различают правое вращение (по часовой стрелке) и левое вращение (против часовой стрелки). Направление вращения луча (относительно луча) не зависит от направления распространения луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл ещё раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации.
| | порядка 0,20. Углы поворота определяют как разности угловых координат.
Для введения модуля в оптическую схему следует поставить соответствующий рейтер на оптическую скамью. При необходимости рейтер может быть закреплен на оптической скамье винтом.
На рейтерах нанесены риски, определяющие положение характерных точек модулей и позволяющие определять координаты этих точек, по шкале оптической скамьи.
| Модуль
| Положение риски
| | М2. микропроектор
| Объектная плоскость линзы микропроектора, она же плоскость размещения объектов в кассете (рис.6).
| | М5. конденсор
| Фокальная плоскость линзы, она же – плоскость экрана.
| | М6. объектив
| Плоскость расположения объектива (тонкая линза).
| | М8. М10. кассеты
| Плоскость размещения объектов в кассетах.
| | М13. Стол поворотный
| Положение центра стола (место размещения объектов).
| 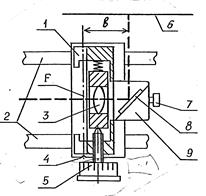
Рис. 6.
| |
|
Лабораторная работа №10
Изучение явления вращения плоскости поляризации света
Цель работы:изучить явление вращения плоскости поляризации света; осовоить метод определения постоянной вращения растворов оптически активных веществ.
Приборы и материалы: модули: кассета в двухкоординатном держателе 8, два идеальных поляризатора 12, стол поворотный 13, мультиметр; объекты: фотодатчик диодный 38, две кюветы 44 с растворами сахара (с известной и неизвестной концентрациями).
Краткая теория
Некоторые вещества, называемые оптически активными, обладают способностью вращения плоскости поляризации проходящего через них плоско поляризованного света (подробнее о поляризации света см. краткую теорию к л.р.№8). К числу таких веществ принадлежат кристаллические тела (например, кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, винной кислоты и др.). Кристаллические вещества сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптической оси кристалла (т.е. отсутствует явление двойного лучепреломления).
Классическим объектом для демонстрации вращения плоскости поляризации служит одноосный кристалл. Схема опыта представлена на рис.10.1. Поляризатор и анализатор установлены так, что не пропускают свет (скрещены).
| | Модуль 2 (микропроектор, рис.6) предназначен для наблюдения на экране установки мелкомасштабных распределений интенсивности и изучаемых объектов, а также для измерения размеров объектов и распределений интенсивности.
На рис.6 приведен вид сверху на этот модуль, установленный на оптической скамье 2. Объекты или распределения интенсивности, расположенные в объектной плоскости кассеты 1, изображаются линзой 3 на экране 6. Необходимый для этого поворот пучка осуществляется отражением от зеркала 8, закрепленного на кронштейне 9.
Для наблюдений в прямом пучке кронштейн 9 с зеркалом можно снять, отвернув два винта 7.
Расстояние b=30 мм полезно знать при «нацеливании» изображения на нужную точку экрана с соблюдением перпендикулярно отраженного пучка по отношению к оптической оси.
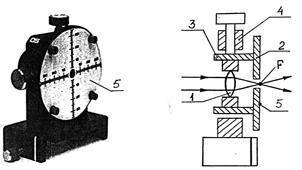 Рис. 7.
Модуль 5 (конденсор, рис.7) содержит короткофокусную линзу 1 и экран 2, расположенный в фокальной плоскости линзы и установленный посредством обоймы 3 в двухкоординатном держателе 4. На экране нанесена двухкоординатная шкала 5. Пучок лазерного излучения собирается в фокусе линзы F, формируя «точечный источник» в плоскости экрана.
Рис. 7.
Модуль 5 (конденсор, рис.7) содержит короткофокусную линзу 1 и экран 2, расположенный в фокальной плоскости линзы и установленный посредством обоймы 3 в двухкоординатном держателе 4. На экране нанесена двухкоординатная шкала 5. Пучок лазерного излучения собирается в фокусе линзы F, формируя «точечный источник» в плоскости экрана.
| |
| 3. После этого при помощи ручки 1 поворотного стола вращайте объект 4(5) по часовой стрелке и наблюдайте за поведением интенсивности отраженного от пластинки пучка. Вы заметите, что интенсивность света при любых значениях угла поворота практически одинакова, даже в окрестности угла Брюстера для исследуемого объекта.
4. Объясните отсутствие зависимости интенсивности отраженного от пластинки луча от угла падения.
Сделайте вывод о проделанной работе.
Контрольные вопросы
1. В чем отличие естественного и поляризованного света?
2. Является ли поляризованным свет солнца, лампы накаливания, люминесцентной лампы, лазера?
3. Выведите формулы Френеля.
4. Выведите закон Брюстера из формул Френеля.
5. Как объяснить закон Брюстера с позиций электронной теории?
6. Докажите, что при падении света на границу раздела двух диэлектриков под углом Брюстера отраженный и преломленный лучи будут взаимно перпендикулярны.
Литература
1. И.В. Савельев. Курс общей физики, т.2
2. Г.С. Ландсберг. Оптика
3. Д.В. Сивухин. Общий курс физики. Оптика.
| |   Рис. 8. Рис. 9.
Модуль 6 (объектив, рис.8) содержит тонкую линзу с фокусным расстоянием F=+100 мм в двухкоординатном держателе. Предназначен для формирования пучков излучения (как правило, совместно с модулем 5) и для опытов по геометрической оптике.
Модуль 8 (рис.9) содержит кассету для установки экранов с изучаемыми объектами в двухкоординатном держателе.
Рис. 8. Рис. 9.
Модуль 6 (объектив, рис.8) содержит тонкую линзу с фокусным расстоянием F=+100 мм в двухкоординатном держателе. Предназначен для формирования пучков излучения (как правило, совместно с модулем 5) и для опытов по геометрической оптике.
Модуль 8 (рис.9) содержит кассету для установки экранов с изучаемыми объектами в двухкоординатном держателе.
  Рис. 10. Рис. 11.
Модуль 10 (рис. 10) содержит кассету, а модуль 12 (рис.11) – поляризатор, которые могут поворачиваться вокруг оптической оси установки. Плоскость поляризатора (т.е. плоскость колебаний вектора
Рис. 10. Рис. 11.
Модуль 10 (рис. 10) содержит кассету, а модуль 12 (рис.11) – поляризатор, которые могут поворачиваться вокруг оптической оси установки. Плоскость поляризатора (т.е. плоскость колебаний вектора | |
|

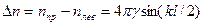 ,
где
,
где 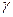 - некоторая константа, а
- некоторая константа, а 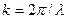 - волновое число. Нетрудно заметить, что при l=0 имеем
- волновое число. Нетрудно заметить, что при l=0 имеем 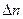 =0, и плоскость поляризации не вращается.
=0, и плоскость поляризации не вращается.
 Рис. 10.6.
Рис. 10.6.
 АСТРАХАНЬ – 2003
АСТРАХАНЬ – 2003
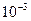 , но возможность выявления в эксперименте чрезвычайно малых
, но возможность выявления в эксперименте чрезвычайно малых 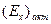 и
и 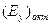 одинаковы. Следовательно, между колебанием вдоль оси х и колебанием вдоль оси у нет сдвига фаз
одинаковы. Следовательно, между колебанием вдоль оси х и колебанием вдоль оси у нет сдвига фаз 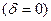 , и в результате сложения этих колебаний получится плоско поляризованная волна. В результате прохождения в активной среде пути z = d плоскость поляризации повернется на угол φ. Из сравнения проекций амплитуды
, и в результате сложения этих колебаний получится плоско поляризованная волна. В результате прохождения в активной среде пути z = d плоскость поляризации повернется на угол φ. Из сравнения проекций амплитуды 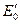 на оси у и х определяем значение угла φ :
на оси у и х определяем значение угла φ :
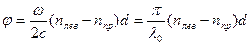 (10.4)
Итак можно считать, что в рамках феноменологической электромагнитной теории света вращение плоскости поляризации получило объяснение. Однако
(10.4)
Итак можно считать, что в рамках феноменологической электромагнитной теории света вращение плоскости поляризации получило объяснение. Однако
 Рис. 10.5.
эта теория не способна объяснить, почему скорость волны в правовращающем веществе отлична от ее скорости в левовращающем (
Рис. 10.5.
эта теория не способна объяснить, почему скорость волны в правовращающем веществе отлична от ее скорости в левовращающем ( 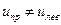 ). Если попытаться ответить на этот вопрос с позиций молекулярной теории, то нужно предположить, что вращение плоскости поляризации связано, с асимметрией строения оптически активного вещества.
). Если попытаться ответить на этот вопрос с позиций молекулярной теории, то нужно предположить, что вращение плоскости поляризации связано, с асимметрией строения оптически активного вещества. 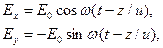
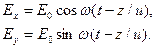 (10.1)
(10.1)  Отсюда вытекает законность разложения плоско поляризованного колебания на два колебания поляризованных по кругу с правым и левым вращением. Для неактивного вещества
Отсюда вытекает законность разложения плоско поляризованного колебания на два колебания поляризованных по кругу с правым и левым вращением. Для неактивного вещества 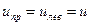 , и если, например,
, и если, например, 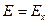 , то обе равные по величине и противоположные по знаку y-компоненты в сумме дадут нуль.
Теперь учтем сделанное выше предположение, что в активном веществе
, то обе равные по величине и противоположные по знаку y-компоненты в сумме дадут нуль.
Теперь учтем сделанное выше предположение, что в активном веществе 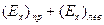 , а y- компонента
, а y- компонента 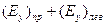 . Вместо
. Вместо 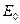 в(10.1) нужно ввести другую амплитуду
в(10.1) нужно ввести другую амплитуду 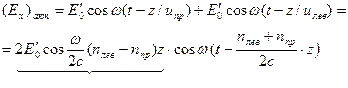 (10.2)
Аналогично для y- компоненты имеем
(10.2)
Аналогично для y- компоненты имеем
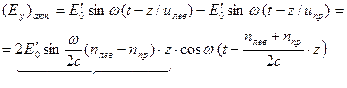 (10.3)
(10.3)
 Рис.1. Общий вид лабораторной установки ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П предназначен для постановки лабораторных работ по оптике в физическом практикуме вузов. Позволяет изучать закономерности геометрической оптики, интерференции, дифракции, поляризации, а также их применение к решению измерительных задач.
Общий вид установки ЛКО-3П приведен на рис.1. Каркас установки состоит из двух боковин 1.1, стянутых оптической скамьей 3, плитой-основанием 1.2 и задней стенкой 1.3. В задней части каркаса размещена кассета с объектами. Вдоль каркаса размещена оптическая скамья 3, состоящая из двух рельс со шкалой (линейкой) с ценой деления 2 мм. Оптическая ось установки расположена симметрично относительно оптической скамьи на высоте 45 мм от верхнего края рельс.
Излучатель 6 (лазер в держателе с 5 степенями свободы) установлен на оптической оси установки над оптической скамьей. С помощью отражателя микропроектора исследуемое излучение направляется на экран, расположенный на задней стенке каркаса.
Рис.1. Общий вид лабораторной установки ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П
Лабораторный оптический комплекс ЛКО-3П предназначен для постановки лабораторных работ по оптике в физическом практикуме вузов. Позволяет изучать закономерности геометрической оптики, интерференции, дифракции, поляризации, а также их применение к решению измерительных задач.
Общий вид установки ЛКО-3П приведен на рис.1. Каркас установки состоит из двух боковин 1.1, стянутых оптической скамьей 3, плитой-основанием 1.2 и задней стенкой 1.3. В задней части каркаса размещена кассета с объектами. Вдоль каркаса размещена оптическая скамья 3, состоящая из двух рельс со шкалой (линейкой) с ценой деления 2 мм. Оптическая ось установки расположена симметрично относительно оптической скамьи на высоте 45 мм от верхнего края рельс.
Излучатель 6 (лазер в держателе с 5 степенями свободы) установлен на оптической оси установки над оптической скамьей. С помощью отражателя микропроектора исследуемое излучение направляется на экран, расположенный на задней стенке каркаса.
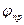 и
и 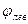 . Отсюда ясно, что плоскость колебаний вектора Е в результирующей плоско поляризованной волне повернется по отношению к направлению колебаний в исходной волне на угол
. Отсюда ясно, что плоскость колебаний вектора Е в результирующей плоско поляризованной волне повернется по отношению к направлению колебаний в исходной волне на угол
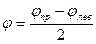 Нетрудно получить основные соотношения для угла поворота плоскости поляризации в привычных обозначениях электромагнитной теории. Если плоско поляризованная волна описывалась выражением
Нетрудно получить основные соотношения для угла поворота плоскости поляризации в привычных обозначениях электромагнитной теории. Если плоско поляризованная волна описывалась выражением
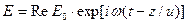 ,
то аналитическое выражение для волны, поляризованной по кругу, нужно записать в виде
,
то аналитическое выражение для волны, поляризованной по кругу, нужно записать в виде
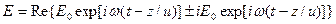 .
Это ясно из того, что круговое колебание всегда можно получить сложением двух взаимно перпендикулярных колебаний равной амплитуды с разностью фаз
.
Это ясно из того, что круговое колебание всегда можно получить сложением двух взаимно перпендикулярных колебаний равной амплитуды с разностью фаз 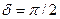 . Так как
. Так как 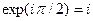 , то появление разности фаз
, то появление разности фаз 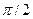 , т.е.
, т.е. 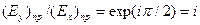 , а при левом вращении Еу отстает от Ех на
, а при левом вращении Еу отстает от Ех на 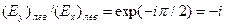 . Следовательно (учитывая, что
. Следовательно (учитывая, что 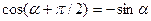 ), имеем:
), имеем:
 Схема излучателя приведена на рис.2. Лазер, смонтированный со схемой стабилизации тока в оправе 5, вставлен в трубу 7, закрепленную подвижно в корпусе 3. Корпус установлен на двух стойках 11. Двумя передними винтами 6 и двумя задними винтами 2 лазер можно перемещать относительно корпуса, подбирая нужное положение и направление пучка излучения. Поляризация излучения – линейная. Плоскость колебаний вектора Е параллельна оси рукоятки 4, с помощью которой лазер поворачивается вокруг оптической оси. Насадка 9 с рассеивающей линзой 10 (объект 42) позволяет получить расходящийся пучок излучения. Насадка крепится на трубе излучателя винтом 8. Питание подается через разъем 1.
Схема излучателя приведена на рис.2. Лазер, смонтированный со схемой стабилизации тока в оправе 5, вставлен в трубу 7, закрепленную подвижно в корпусе 3. Корпус установлен на двух стойках 11. Двумя передними винтами 6 и двумя задними винтами 2 лазер можно перемещать относительно корпуса, подбирая нужное положение и направление пучка излучения. Поляризация излучения – линейная. Плоскость колебаний вектора Е параллельна оси рукоятки 4, с помощью которой лазер поворачивается вокруг оптической оси. Насадка 9 с рассеивающей линзой 10 (объект 42) позволяет получить расходящийся пучок излучения. Насадка крепится на трубе излучателя винтом 8. Питание подается через разъем 1.
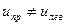 . В силу этого все оптически активные вещества можно подразделить на «правые» (
. В силу этого все оптически активные вещества можно подразделить на «правые» ( 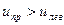 ) и «левые» (
) и «левые» ( 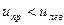 ).
).
 Рис. 10.4.
Рассмотрим, что произойдет с плоско поляризованной волной, распространяющейся в оптически активной среде. Разложим исходную волну Е на две волны, поляризованные по правому и левому кругу, скорости распространения которых в данном веществе не равны. Очевидно, что время, необходимое каждой волне для прохождения одного и того же отрезка в исследуемой активной среде, окажется различным. Следовательно, векторы Епр и Елев повернутся на различные углы
Рис. 10.4.
Рассмотрим, что произойдет с плоско поляризованной волной, распространяющейся в оптически активной среде. Разложим исходную волну Е на две волны, поляризованные по правому и левому кругу, скорости распространения которых в данном веществе не равны. Очевидно, что время, необходимое каждой волне для прохождения одного и того же отрезка в исследуемой активной среде, окажется различным. Следовательно, векторы Епр и Елев повернутся на различные углы  Рис. 3.
В комплексе ЛКО-3П установлен регулируемый стабилизированный источник тока для лазерного излучателя (рис.3). Разъем питания лазера соединен кабелем с разъемом «ЛАЗЕР» источника тока. К разъему питания «ПИТ» источника тока подключен переносной блок питания.
Ручкой «ТОК» регулируют ток лазера в пределах 20 – 60 мА. Для измерения тока измеряют выведенное на гнезда “U/R” напряжение U на резисторе R=100 Ом, включенном последовательно с лазером. Ток лазера I=U/R.
Функциональные модули
При выполнении лабораторных работ на комплексе ЛКО-3П используются 8 функциональных модулей.
Функциональные модули размещены и установлены на рейтерах (двухкоординатном и поворотном держателях). Рейтеры обеспечивают установку модулей на оптической скамье и перемещение модулей вдоль оптической скамьи. Держатели обеспечивают юстировочные перемещения модулей. Номера модулей нанесены на их корпусах.
Рис. 3.
В комплексе ЛКО-3П установлен регулируемый стабилизированный источник тока для лазерного излучателя (рис.3). Разъем питания лазера соединен кабелем с разъемом «ЛАЗЕР» источника тока. К разъему питания «ПИТ» источника тока подключен переносной блок питания.
Ручкой «ТОК» регулируют ток лазера в пределах 20 – 60 мА. Для измерения тока измеряют выведенное на гнезда “U/R” напряжение U на резисторе R=100 Ом, включенном последовательно с лазером. Ток лазера I=U/R.
Функциональные модули
При выполнении лабораторных работ на комплексе ЛКО-3П используются 8 функциональных модулей.
Функциональные модули размещены и установлены на рейтерах (двухкоординатном и поворотном держателях). Рейтеры обеспечивают установку модулей на оптической скамье и перемещение модулей вдоль оптической скамьи. Держатели обеспечивают юстировочные перемещения модулей. Номера модулей нанесены на их корпусах.
 Рис. 10.2.
Рис. 10.2.
 Рис. 10.3.
Эксперименты, подобные описанным выше, легли в основу метода определения концентрации оптически активного вещества путем измерения угла поворота плоскости поляризации. Данный метод имеет многочисленные практические приложения — в частности им пользуются для определения концентрации сахара в производственных растворах и биологических объектах (кровь, моча).
Интерпретация вращения плоскости поляризации была дана впервые Френелем. При изложении сущности формальной теории Френеля прежде всего установим, что любое плоско поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением. Это ясно из геометрического построения, приведенного на рис.10.3. Действительно, сумма двух векторов
Рис. 10.3.
Эксперименты, подобные описанным выше, легли в основу метода определения концентрации оптически активного вещества путем измерения угла поворота плоскости поляризации. Данный метод имеет многочисленные практические приложения — в частности им пользуются для определения концентрации сахара в производственных растворах и биологических объектах (кровь, моча).
Интерпретация вращения плоскости поляризации была дана впервые Френелем. При изложении сущности формальной теории Френеля прежде всего установим, что любое плоско поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением. Это ясно из геометрического построения, приведенного на рис.10.3. Действительно, сумма двух векторов  Рис. 4.
Двухкоординатный держатель (рис.4) состоит из корпуса 1 и обоймы 2, удерживаемой пружинами 3 и перемещаемой двумя винтами 4 и 5 в пределах 2 мм от среднего положения по горизонтали и по вертикали. Корпус закреплен на рейтере 6. обойма может поворачиваться на произвольный угол округ горизонтальной оси (оптической оси установки). Такие держатели имеют модули 5,6,8.
Рис. 4.
Двухкоординатный держатель (рис.4) состоит из корпуса 1 и обоймы 2, удерживаемой пружинами 3 и перемещаемой двумя винтами 4 и 5 в пределах 2 мм от среднего положения по горизонтали и по вертикали. Корпус закреплен на рейтере 6. обойма может поворачиваться на произвольный угол округ горизонтальной оси (оптической оси установки). Такие держатели имеют модули 5,6,8.
 Рис. 5.
Поворотный держатель (рис.5) состоит из корпуса 1 и обоймы 2, соединенной с круговой шкалой 3. Поворот обоймы вокруг оси О-О производится рукояткой 4. Отсчет угловых координат производится по основной шкале 3 (цена деления 20) и нониусу 5 (цена деления 0,50). Рычаг 6 поворачивают до совпадения его горизонтальной риски с одним из делений основной шкалы и снимают отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10 при погрешности
Рис. 5.
Поворотный держатель (рис.5) состоит из корпуса 1 и обоймы 2, соединенной с круговой шкалой 3. Поворот обоймы вокруг оси О-О производится рукояткой 4. Отсчет угловых координат производится по основной шкале 3 (цена деления 20) и нониусу 5 (цена деления 0,50). Рычаг 6 поворачивают до совпадения его горизонтальной риски с одним из делений основной шкалы и снимают отсчет по нониусу. Таким методом можно снимать отсчеты с разрешением 0,10 при погрешности  Рис. 10.1.
После введения между поляризатором и анализатором пластинки кварца толщиной d свет начинает проходить через данную оптическую систему. Свет распространяется вдоль оптической оси кварца. Повернув анализатор на угол
Рис. 10.1.
После введения между поляризатором и анализатором пластинки кварца толщиной d свет начинает проходить через данную оптическую систему. Свет распространяется вдоль оптической оси кварца. Повернув анализатор на угол 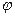 , снова получаем темноту. Опыт даёт
, снова получаем темноту. Опыт даёт 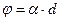 , где d – путь луча, пройденный в кристалле и α - удельная постоянная вращения, причем αсильно зависит от длины волны
, где d – путь луча, пройденный в кристалле и α - удельная постоянная вращения, причем αсильно зависит от длины волны 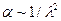 .
В опытах с растворами все выполняется также как и в предыдущем случае, но вместо кварца между поляризаторами вводится кювета с раствором оптически активного вещества. Если обозначить длину кюветы через d, концентрацию вещества через с, то из опыта следует:
.
В опытах с растворами все выполняется также как и в предыдущем случае, но вместо кварца между поляризаторами вводится кювета с раствором оптически активного вещества. Если обозначить длину кюветы через d, концентрацию вещества через с, то из опыта следует: 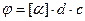 , где [α] - удельная постоянная вращения для данного вещества. Она также сильно зависит от длины волны (
, где [α] - удельная постоянная вращения для данного вещества. Она также сильно зависит от длины волны ( 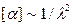 ) и слабо от температуры раствора.
Опыт показывает, что разные модификации одного оптически активного кристаллического вещества (например, разные образцы кварца) вращают плоскость поляризации вправо или влево (если смотреть навстречу световому лучу). Таким образом, различают правое вращение (по часовой стрелке) и левое вращение (против часовой стрелки). Направление вращения луча (относительно луча) не зависит от направления распространения луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл ещё раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации.
) и слабо от температуры раствора.
Опыт показывает, что разные модификации одного оптически активного кристаллического вещества (например, разные образцы кварца) вращают плоскость поляризации вправо или влево (если смотреть навстречу световому лучу). Таким образом, различают правое вращение (по часовой стрелке) и левое вращение (против часовой стрелки). Направление вращения луча (относительно луча) не зависит от направления распространения луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл ещё раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации.

 Рис. 7.
Модуль 5 (конденсор, рис.7) содержит короткофокусную линзу 1 и экран 2, расположенный в фокальной плоскости линзы и установленный посредством обоймы 3 в двухкоординатном держателе 4. На экране нанесена двухкоординатная шкала 5. Пучок лазерного излучения собирается в фокусе линзы F, формируя «точечный источник» в плоскости экрана.
Рис. 7.
Модуль 5 (конденсор, рис.7) содержит короткофокусную линзу 1 и экран 2, расположенный в фокальной плоскости линзы и установленный посредством обоймы 3 в двухкоординатном держателе 4. На экране нанесена двухкоординатная шкала 5. Пучок лазерного излучения собирается в фокусе линзы F, формируя «точечный источник» в плоскости экрана.

 Рис. 8. Рис. 9.
Модуль 6 (объектив, рис.8) содержит тонкую линзу с фокусным расстоянием F=+100 мм в двухкоординатном держателе. Предназначен для формирования пучков излучения (как правило, совместно с модулем 5) и для опытов по геометрической оптике.
Модуль 8 (рис.9) содержит кассету для установки экранов с изучаемыми объектами в двухкоординатном держателе.
Рис. 8. Рис. 9.
Модуль 6 (объектив, рис.8) содержит тонкую линзу с фокусным расстоянием F=+100 мм в двухкоординатном держателе. Предназначен для формирования пучков излучения (как правило, совместно с модулем 5) и для опытов по геометрической оптике.
Модуль 8 (рис.9) содержит кассету для установки экранов с изучаемыми объектами в двухкоординатном держателе.

 Рис. 10. Рис. 11.
Модуль 10 (рис. 10) содержит кассету, а модуль 12 (рис.11) – поляризатор, которые могут поворачиваться вокруг оптической оси установки. Плоскость поляризатора (т.е. плоскость колебаний вектора
Рис. 10. Рис. 11.
Модуль 10 (рис. 10) содержит кассету, а модуль 12 (рис.11) – поляризатор, которые могут поворачиваться вокруг оптической оси установки. Плоскость поляризатора (т.е. плоскость колебаний вектора