
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Круговая поляризация
Круговая поляризация

Пустm два когерентных пучка совмещаются, причем поляризации перпендикулярны.

 если разность фаз =0 , то вектор результирующего поля будет под углом:
если разность фаз =0 , то вектор результирующего поля будет под углом:
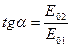 и если
и если 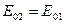 , то
, то  .
.
Таким образом, результирующий пучок света является плоскопараллельным.
Если же сдвиг по фазе =  , то при х=0
, то при х=0 
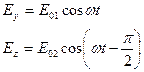
В последовательные моменты времени:
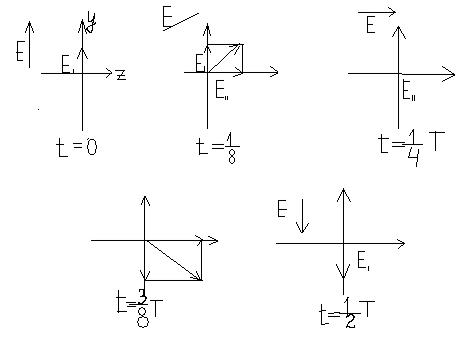
Таким образом, результирующий вектор 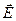 остается постоянным по величине и вращается по часовой стрелке вокруг х. такая поляризация называется левой круговой.
остается постоянным по величине и вращается по часовой стрелке вокруг х. такая поляризация называется левой круговой.
Если смещать пучки одинаковой интенсивности один, из которых имеет левую, а другой правую круговую поляризацию, то в результате получим плоскополяризованный пучок (отдельные фотоны имеют круговую поляризацию).
Если сложить два колебания с разными амплитудами, имеющий разность фаз, то результирующий вектор Е будет вращаться, скользя по эллипсу, т.е эллиптическая поляризация.
Поляризаторы и анализаторы
Пучок неполяризованного света можно поляризовать, если пропустить его через поляризатор.
Рассмотрим сначала для микроволн. Экран, изготовленный из тонких параллельных проволочек является ,в этом случае хорошим поляризатором.
Если пучок микроволнового излучения поляризовать вертикально и проволочки тоже натянуть вертикально, то в каждой проволочке индуцируется ток I.
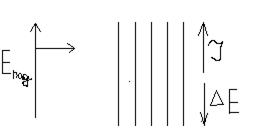
Индуцированный ток излучает поля  . Поэтому справа от поляризатора результирующее поле
. Поэтому справа от поляризатора результирующее поле 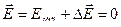 и поляризатор ведет себя как отражатель, который не пропускает пучок. Если же проволочки перпендикулярны
и поляризатор ведет себя как отражатель, который не пропускает пучок. Если же проволочки перпендикулярны 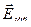 , то вертикальным токам «негде» индуцировать. Поэтому не возникает дополнительного излучения и падающая волна проходит без искажений. Примем за ось поляризатора перпендикуляр к линии, в направлении которой расположены проволочки.
, то вертикальным токам «негде» индуцировать. Поэтому не возникает дополнительного излучения и падающая волна проходит без искажений. Примем за ось поляризатора перпендикуляр к линии, в направлении которой расположены проволочки.

 Поляризатор будет излучать поля
Поляризатор будет излучать поля  под прямым углом к оси. Поскольку
под прямым углом к оси. Поскольку  компенсирует составляющую поля
компенсирует составляющую поля 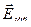 в этом направлении, то результирующее поле Е будет представлять собой составляющую поля
в этом направлении, то результирующее поле Е будет представлять собой составляющую поля 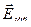 параллельную оси и
параллельную оси и  или
или 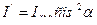
Таким образом  , случай идеального поляризатора интенсивность пропорциональна
, случай идеального поляризатора интенсивность пропорциональна  , где α- угол между плоскостью поляризации света и осью поляризатора (закон Малика).
, где α- угол между плоскостью поляризации света и осью поляризатора (закон Малика).
Излучение после прохождения поляризатора оказывается плоскополяризованный в направлении оси поляризатора. На этом же принципе основано действие светового поляроидного фильтра. Он изготавливается из вещества, состоящего из длинных параллельных цепочек молекул, вдоль которых может течь электрический ток. В случае неполяризованного света составляющие поля 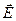 параллельны цепочкам поглощаются и в пучке остаются лишь те составляющие поля, которые параллельны оси поляризатора.
параллельны цепочкам поглощаются и в пучке остаются лишь те составляющие поля, которые параллельны оси поляризатора.
Например, кристалл турмалина пропускает лишь волны, для которых 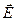 параллельны оси кристалла. Поэтому происходит ослабление интенсивности неполяризованного света в 2раза и свет становиться поляризованным.
параллельны оси кристалла. Поэтому происходит ослабление интенсивности неполяризованного света в 2раза и свет становиться поляризованным.

Если взять два кристалла, то до второго доходит поляризованный свет и в зависимости от ориентации через второй кристалл проходит часть потока согласно закону Малюса. Явлении поляризации света имеет место и при отражении им преломлении света на границе двух диэлектриков. Видно усиление и ослабление света за пластинкой турмалина.
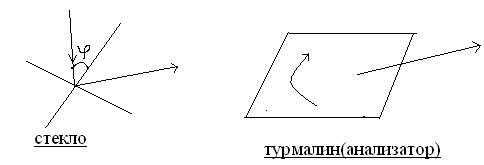
Можно использовать два зеркала (стекло)
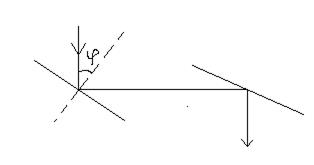
Изменяя угол наклона зеркала к лучу можно убедиться, что доля поляризованного света зависит от угла падения φ. При определенном угле падения отраженный луч оказывается полностью поляризованным  (закон Брюстера 1815 г.)
(закон Брюстера 1815 г.)
Формулы Френеля
Рассчитаем амплитуды и фазы, отраженных о границы раздела диэлектриков световых волн и волн, прошедших через границу раздела.
Два подхода:
1) можно детально рассмотреть воздействие световой волны на электрические заряды атомов среды. Электромагнитные волны возбуждают их колебания, и затем излучение вторичных волн. Их интерференция с волной, падающей, на среду приводит, к возникновению отраженной и преломленной волн. Но решение задачи очень громоздко.
2) Из решения системы уравнений Максвелла. Свойства среды при этом задаются её 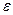 .
.
Граничные условия для электромагнитного поля для тангенциальных компонент

В первой среде результирующее значение поля вблизи границы = сумме полей падающей и отраженной волн, а внутри второй среды – лишь полем проходящей волны.
- для тонких волн

а)  повернуты на π, т.к. при отражении скачок фазы =π.
повернуты на π, т.к. при отражении скачок фазы =π.

б) целесообразно рассматривать два случая, когда 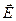 либо лежит в плоскости падения, либо перпендикулярно к ней.
либо лежит в плоскости падения, либо перпендикулярно к ней. 
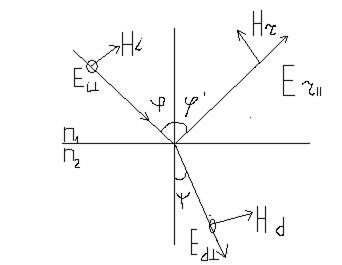
Результаты вычисления 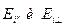 позволяют решить задачу от отражений и преломлений света произвольной поляризации.
позволяют решить задачу от отражений и преломлений света произвольной поляризации.
Для случая а) граничные условия будут:
Тангенциальная составляющая  (*)
(*)
Нормальная составляющая терпит разрыв  (**)
(**)
Из закона преломления
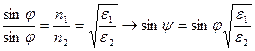
Тогда из (**):
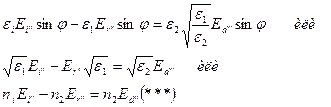
Из (*):

A из (***):
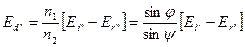
Приравнивая, получим:
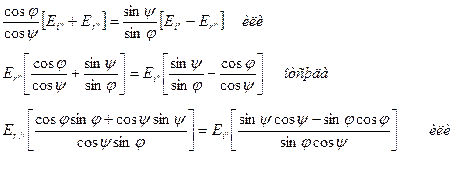
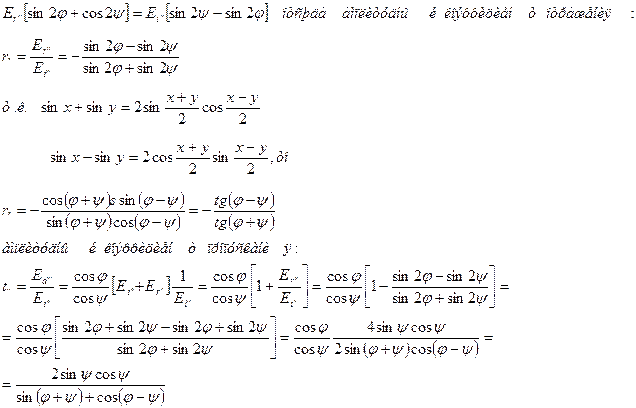 Для компонент перпендикуляра плоскости падения (случай б) граничные условия будут:
Для компонент перпендикуляра плоскости падения (случай б) граничные условия будут:
Тангенциальная составляющая 
Нормальная составляющая 
Второе условие получено для магнитного вектора с учетом того, что 
 и для тангенциальной составляющей Н.
и для тангенциальной составляющей Н.
Аналогично выше изложенному:

Формулы Френеля дают возможность рассчитать амплитуду каждой из компонент 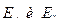 . Поэтому они содержат полное решение задачи о степени поляризации отраженного и преломленного света, за меру степени поляризации принимается
. Поэтому они содержат полное решение задачи о степени поляризации отраженного и преломленного света, за меру степени поляризации принимается

Физический смысл закона Брюстера.
При выводе формул Френеля мы пользовались граничными условиями для электромагнитного поля, не прибегая к представлениям о вторичных волнах, испускаемых атомами. Привлечем эти рассуждения для истолкования закона Брюстера:

Падающая волна возбуждает в среде 2 колебания электрические, которые становятся источниками вторичных волн, которые и дают отраженный свет. Направление колебания совпадает с направлением электрического вектора световой волны. Т.е. для среды 2 оно перпендикулярна к ОС. Представим это колебание как сумму двух колебаний 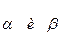 перпендикулярных к друг другу. т.е. мы изображаем колебания эл. в молекуле как суперпозицию колебаний 2-х элементарных излучателей, оси которых направлены по
перпендикулярных к друг другу. т.е. мы изображаем колебания эл. в молекуле как суперпозицию колебаний 2-х элементарных излучателей, оси которых направлены по 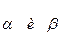 .
.
Пусть свет падает под углом Брюстера, т.е.  . тогда ОВ перпендикулярна ОС, т.е. ОВ параллельна α. Но колеблющийся заряд не излучает электромагнитных волн вдоль направления своего движения. Таким образом, по направлению ОВ идет свет посылаемый излучателями типа β, направление колебания которых перпендикулярна ОВ. Таким образом, отраженный свет, оказывается полностью поляризован, перпендикулярно плоскости падения.
. тогда ОВ перпендикулярна ОС, т.е. ОВ параллельна α. Но колеблющийся заряд не излучает электромагнитных волн вдоль направления своего движения. Таким образом, по направлению ОВ идет свет посылаемый излучателями типа β, направление колебания которых перпендикулярна ОВ. Таким образом, отраженный свет, оказывается полностью поляризован, перпендикулярно плоскости падения.
Двойное лучепреломление.
Большой интерес представляет рассмотрение особенностей прохождения света через некоторые кристаллы, называемые двоякопреломляющими. Узкий пучок света, проходя через плоскопараллельную пластину такого кристалла, например исландского шпата ( 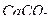 ), раздваивается (даже при нулевом угле падения). Если вращать такой кристалл вокруг падающего угла, то один из лучей остается неподвижным (обыкновенный луч), а другой поворачивается вокруг первого (необыкновенный луч), хотя углом падения при этом не меняется. На выходе лучи оказываются линейно поляризованными во взаимно перпендикулярных плоскостях.
), раздваивается (даже при нулевом угле падения). Если вращать такой кристалл вокруг падающего угла, то один из лучей остается неподвижным (обыкновенный луч), а другой поворачивается вокруг первого (необыкновенный луч), хотя углом падения при этом не меняется. На выходе лучи оказываются линейно поляризованными во взаимно перпендикулярных плоскостях.
В кристалле можно найти такое направление, вдоль которого раздвоение нормально падающего луча отсутствует - это оптическая ось кристалла. плоскость содержащая оптическую ось и падающий луч называется главной плоскостью (главным сечением) для данного луча. Особенность падения светового луча в кристалле связаны с его анизотропией. Значение  , а следовательно и скорости распространения света
, а следовательно и скорости распространения света  (и показателя преломления n) также неодинаковы.
(и показателя преломления n) также неодинаковы.
Для одноосного кристалла (если х соответствует оптической оси):

Таким образом, направление векторов  в отличие от изотропной среды уже не совпадают друг с другом.
в отличие от изотропной среды уже не совпадают друг с другом.  (нормаль к волновому фронту).
(нормаль к волновому фронту).

 (вектор Умова-Пойптинга)
(вектор Умова-Пойптинга)

Все это усложняет рассмотрения условий распространения света. Поэтому ограничимся лишь простейшими случаями.
а) 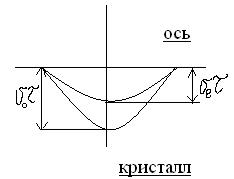 б)
б) 
Пусть узкий пучок света падает перпендикулярно на поверхность кристалла, у которого оптическая ось параллельна поверхности тогда плоскости чертежа являются главной плоскостью данного луча.
По Гюйгенсу вторичный волновой фронт обыкновенного луча изобразиться полуокружностью радиуса  , где
, где  - время распространения луча в кристалле. Волновой фронт необыкновенного луча изобразится полуэллипсом. Если необыкновенный луч распространяется медленно, то полуэллипс вписан в полуокружность (а) имея точки касания с ней по концам диаметра (т.е. на оптической оси). Такой кристалл называется положительным. Если же скорость необыкновенного луча больше чем обыкновенного (отрицательный кристалл), то полуокружность оказывается вписанной в полуэллипс (б).
- время распространения луча в кристалле. Волновой фронт необыкновенного луча изобразится полуэллипсом. Если необыкновенный луч распространяется медленно, то полуэллипс вписан в полуокружность (а) имея точки касания с ней по концам диаметра (т.е. на оптической оси). Такой кристалл называется положительным. Если же скорость необыкновенного луча больше чем обыкновенного (отрицательный кристалл), то полуокружность оказывается вписанной в полуэллипс (б).
Разность между  довольно значительно. Например, для исландского шпата
довольно значительно. Например, для исландского шпата  ; для кварца
; для кварца  .
.
Если вращать чертеж вокруг падающего луча, то полуокружность станет полусферой, а полуэллипс - полуэллипсом вращения.
Рассмотрим некоторые простые случаи:
а) луч параллельна оптической оси. Условия распространения лучей с любой поляризацией одинаковы и они не раздваиваются.

б) Луч перпендикулярна оси. Электромагнитный вектор, лежащий в главной плоскости параллельно оси. Электромагнитный вектор  оси лежит при этом в плоскости
оси лежит при этом в плоскости  к главной. Поэтому условия распространения для этих составляющих электрического поля световой волны неодинаковы: лучи не раздваиваются, но имеют разную скорость распространения.
к главной. Поэтому условия распространения для этих составляющих электрического поля световой волны неодинаковы: лучи не раздваиваются, но имеют разную скорость распространения.
в) Если луч идет под углом к оси, то условия распространения составляющих также неодинаковы: лучи распространяются по различным направлениям и с разными скоростями.
Легко видеть, что луч с электрическим вектором  оси во всех случаях находиться в одинаковых условиях, так что законы его распространения не меняются. Это и есть обыкновенный луч.
оси во всех случаях находиться в одинаковых условиях, так что законы его распространения не меняются. Это и есть обыкновенный луч.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|