Геометрическая оптика как предельный случай волновой оптики.

Геометрическая оптика как предельный случай волновой оптики.

Наблюдения показывают, что в свободном пространстве свет от точечного источника Р в точку А распространяется по прямой линии.

С точки зрения волновой оптики это можно объяснить:

Согласно принципу Гюгенса-Френеля амплитуда электромагнитного поля в точке А равна сумме амплитуд волн от вторичных сферических источников расположенных на вспомогательной поверхности Е, разбитой на зоны Френеля. Из диаграммы Френеля следует, что результирующая амплитуда в А в два раза меньше амплитуды поля создаваемого лишь первой зоной Френеля с радиусом . Таким образом, поля в А в основном определяется первой зоной. Так как выбор вспомогательной поверхности произволен, то можно представить себе на пути от Р к А множества таких поверхностей в каждой из которых определена своя первая зона Френеля.

Мысленно соединим центры первых зон линией, а края отдельных зон соединим поверхностью. Форма такой поверхности похожа на сильно вытянутый эллипсоид с осью РА. Приняв а+b=с=соnst получим 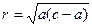и при будет max.

Ясно, что внутри объема, ограниченного эллипсоидом (объем Френеля) в основном и распространяется свет. Радиусы поперечных сечений объема Френеля ~ 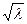и предельном случае λ→0 объем Френеля стягивается в линию, которую и называют лугом света. С физической точки зрения луч света- это жгут с поперечным размером равным размеру первой зоны Френеля. В пределах этой области поля световой волны, амплитуда которой равна амплитуде поля в пределах первой зоны Френеля, а фаза равна фазе поля в этой же области. Ясно, что при этом реальные изменения амплитуды и фазы поля в направлении перпендикулярно направлению распространения света очень малы const. Таким образом, амплитуда поля распространяющегося вдоль луча может быть выражена . Величину Ф(xyz) называют эйконал(от греческого - изображение).

Из волнового уравнения при λ→0 можно получить уравнение для определения и Ф. Из этих уравнений следует, что лучи распространяются по нормам к поверхности равного эйконала или равной фазы, называемых волновыми поверхностями. Для изохронных сред форма волновой поверхности совпадает с фронтами волны.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒