
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Принцип Ферма. Законы отражения и преломления.
Принцип Ферма. Законы отражения и преломления.
В предельном случае перехода к геометрической оптике (λ→0) распространения волнового фронта может быть найдено простым построением. В каждой точке волнового фронта построим сферу с радиусом 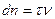 ,где
,где  - скорость волны,
- скорость волны, 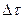 -б/м промежуток времени. Поверхность
-б/м промежуток времени. Поверхность  огибающая эти сферы также есть поверхность равной фазы , так как все точки её будут иметь к моменту
огибающая эти сферы также есть поверхность равной фазы , так как все точки её будут иметь к моменту 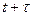 те же фазы, что и точки поверхности F к моменту t. Отрезки прямых dn соединяющие точки фронта F
те же фазы, что и точки поверхности F к моменту t. Отрезки прямых dn соединяющие точки фронта F
С точкой касания соответствующей сферы и огибающей, представляют собой элементы луча, перпендикулярные к поверхности фронта.
Продолжая построения можно шаг за шагом определить поверхность равной фазы и в то же время найти направление лучей (из отрезков dn). Таким образом, действительный путь распространениясвета (луч) есть путь, для нахождения которого свету требуется min время по сравнению с любым другим мыслимым путем между теми же точками.
Действительно от А до В вдоль луча свет проходит за время 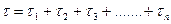 , где
, где 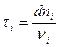 т.е.
т.е.
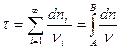
Всякий другой путь больше и 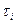 отличается, больше, чем при распространении по нормам. Таким образом, действительно путь распространения света (луч) соответствует min времени распространения (принцип Френеля).
отличается, больше, чем при распространении по нормам. Таким образом, действительно путь распространения света (луч) соответствует min времени распространения (принцип Френеля).
Эта теорема в геометрической оптике представляет аксиому, сформулированную Ферма (1660г.) как общий закон распространения света.
Для однородной среды этот принцип приводит к закону прямолинейного распространения согласно геометрической аксиоме о том, что прямая есть кратчайшее расстояние между двумя точками.
Для случая перехода через границу различных сред этот принцип дает законы отражения и преломления света. Любой путь 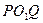 лежащей вне плоскости падения проходиться светом за большее время, чем путь POQ проведенный в плоскости падения. И в согласии с принципом Ферма путь, требующий минимального времени должен лежать в плоскости падения (т.е плоскости перпендикулярна к границе раздела и проходящая через P и Q).
лежащей вне плоскости падения проходиться светом за большее время, чем путь POQ проведенный в плоскости падения. И в согласии с принципом Ферма путь, требующий минимального времени должен лежать в плоскости падения (т.е плоскости перпендикулярна к границе раздела и проходящая через P и Q).
Таким образом, получим первый закон преломления.
Чтобы из всех путей от Р до Q лежащих в плоскости падения выбрать путь, требующий min времени, исследуем как меняется это время в зависимости от положения точки О.
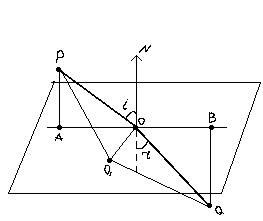
Путь АО=х; РА= 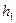 ; QB=
; QB= 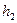 ; AB=P; OB=P-x.
; AB=P; OB=P-x.
Время распространения света по пути POQ будет:
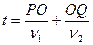 , где
, где  скорости света в этих средах.
скорости света в этих средах.
Или 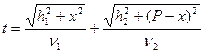
Условие min времени есть 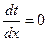 т.е.
т.е.
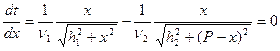
или 
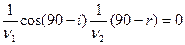
т.е. 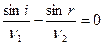 или
или 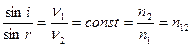 относительный показатель преломления среды 2 относительно среды 1.
относительный показатель преломления среды 2 относительно среды 1.
Абсолютный показатель 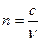 .
.
Для малых углов закон преломления 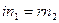 .
.
При формальной замене 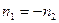 получаем закон отражения
получаем закон отражения 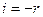 . Таким образом, любую формулу, выведенную для преломляющих систем можно использовать для описания явлений в отражающих системах.
. Таким образом, любую формулу, выведенную для преломляющих систем можно использовать для описания явлений в отражающих системах.
Понятие: Если пучок лучей имеет одну общую вершину, то его называют гомоцентрическим.
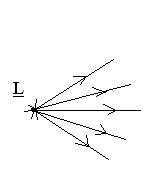
Если после отражения и преломления это пучок превращается в пучок, сходящийся также в точку, то гомоцентричность сохраняется и эта точка 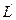 сопряжена с L, или является изображением точки L.
сопряжена с L, или является изображением точки L.
 Систему,сохраняющую гомоцентричность пучка называют стигматической.В противном случае – астигматической.
Систему,сохраняющую гомоцентричность пучка называют стигматической.В противном случае – астигматической.
 Так как в практической оптике обычно ставиться задача получения изображений, точно передающих форму источника, то важнейшим вопросом лучевой оптики является выяснение условий сохранения гомоцентричности пучков.
Так как в практической оптике обычно ставиться задача получения изображений, точно передающих форму источника, то важнейшим вопросом лучевой оптики является выяснение условий сохранения гомоцентричности пучков.
Отражение и преломление света на плоской границе раздела. Призмы. Световоды.
Луч света, достигнув плоской границы раздела 2-х сред частично отражается частично проходит, неиспытывая преломление.
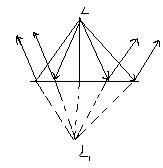 так как угол падения равен углу отражения, то гомоцентричность отражения лучей сохраняется. Лучи сойдутся на расстоянии а от границы раздела( если их продолжить назад). Т.е. плоская граница создает мнимое изображение точечного источника. Если источник протяженный, то каждой точке его поверхности будет соответствовать свое изображение и изображение источника будет прямым и мнимым.
так как угол падения равен углу отражения, то гомоцентричность отражения лучей сохраняется. Лучи сойдутся на расстоянии а от границы раздела( если их продолжить назад). Т.е. плоская граница создает мнимое изображение точечного источника. Если источник протяженный, то каждой точке его поверхности будет соответствовать свое изображение и изображение источника будет прямым и мнимым.
Для преломленных лучей гомоцентричноть пучка нарушается. Это связано с тем, что по закону преломления пропорциональны между собой не значения углов падения и преломления, а их синусы. Но если углы падения малы, то гомоцентричность пучков при преломлении практически сохраняется. При наблюдении из оптически более плотной среды будет казаться, что источник света находиться на расстоянии 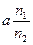 от границы раздела; а из менее оптически плотной среды кажется, что на расстоянии
от границы раздела; а из менее оптически плотной среды кажется, что на расстоянии 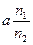 . Именно поэтому нам кажется, что предметы, находящиеся в воде. Как бы уменьшаются в размерах.
. Именно поэтому нам кажется, что предметы, находящиеся в воде. Как бы уменьшаются в размерах.
Из закона преломления, примененного к случаю падения луча из оптически более плотной сферы (скорость света 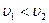 ) следует, что угол преломления больше угла падения
) следует, что угол преломления больше угла падения 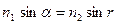
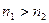 .
.
Но если угол падения удовлетворяет условию 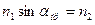 или
или 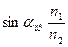 , то угол преломления равен
, то угол преломления равен 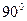 , т.е. преломленный луч скользит по границе раздела. Такой угол называется предельным. При дальнейшем увеличении угла падения проникновение луча вглубь второй среды прекращается и наступает полное отражение.
, т.е. преломленный луч скользит по границе раздела. Такой угол называется предельным. При дальнейшем увеличении угла падения проникновение луча вглубь второй среды прекращается и наступает полное отражение.
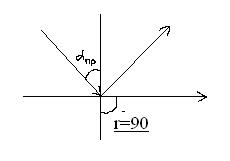 строгое рассмотрение вопроса с волновой точки зрения показывает, что в действительности волна проникает во вторую среду на глубину ~λ.
строгое рассмотрение вопроса с волновой точки зрения показывает, что в действительности волна проникает во вторую среду на глубину ~λ.
Полное отражение находит различные практические применения.
Так как для системы стекло-воздух 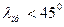 то призмы позволяют изменять ход луча так, что отражение происходи почти без потерь.
то призмы позволяют изменять ход луча так, что отражение происходи почти без потерь.
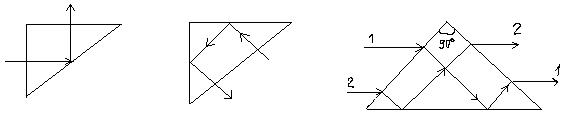
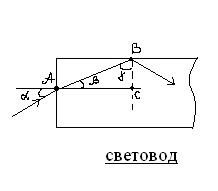
Если ввести свет в тонкую стеклянную трубку с её торца, то испытывая на стенках полное отражение, луч будет следовать вдоль трубки даже при сложных её изгибах. На этом принципе работают световоды – тонкие прозрачные волокна, позволяющие проводить световой пучок по искривленному пути (волоконная оптика). Луч, вошедший в световод по углом α встретит поверхность световода по углом 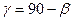 , где
, где 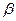 - угол преломления. Чтобы при этом возникло полное отражение надо чтобы
- угол преломления. Чтобы при этом возникло полное отражение надо чтобы 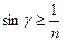 , где n – показатель преломления световода.
, где n – показатель преломления световода.
Так как 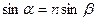 или
или 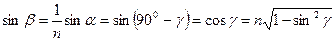 , но так как
, но так как 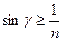 , то
, то  . Пологая , что
. Пологая , что 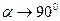 получим
получим 
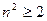 . Таким образом, даже при почти скользящем падении луч испытывает в световоде полное отражение если
. Таким образом, даже при почти скользящем падении луч испытывает в световоде полное отражение если 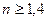 . В действительности световод набирается из тонких гибких волокон с n, окруженных оболочкой с
. В действительности световод набирается из тонких гибких волокон с n, окруженных оболочкой с 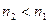 .
.
Каждое волокно передает по световоду небольшой участок изображения, получающее на выходе световода.
Призма.
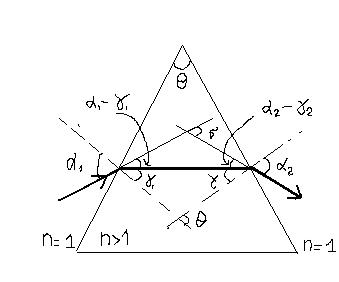
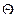 - преломляющий угол
- преломляющий угол
б - угол отклонения луча;
так как б- внешний угол ∆,то 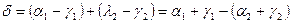
но 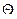 так же есть внешний угол другого ∆ и поэтому
так же есть внешний угол другого ∆ и поэтому 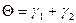 , т.е.
, т.е. 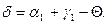 так как
так как 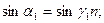
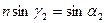 , то Исследуем на экстремум функцию угла отклонения луча. Беря производную от б по γ, и приравняв к нулю:
, то Исследуем на экстремум функцию угла отклонения луча. Беря производную от б по γ, и приравняв к нулю: 
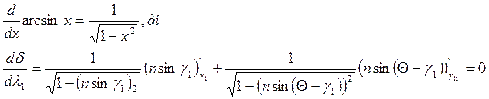
Или
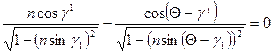 . Если
. Если 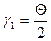 , то это удовлетворяется; а так как
, то это удовлетворяется; а так как 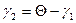 , то
, то 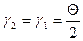
 , т.е. ход лучей должен быть симметричным. При этом получается min угол отклонения, так как при
, т.е. ход лучей должен быть симметричным. При этом получается min угол отклонения, так как при 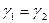 и
и 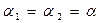 , т.е.
, т.е. 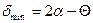 . Отсюда
. Отсюда 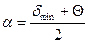 , а так как
, а так как 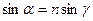 , то
, то 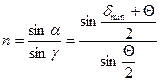
Это уравнение применяется для определения n по углу минимального отклонения.
Опыт показывает, что стеклянные призмы сильнее преломляют коротковолновую часть спектра (синие лучи), и что нет линейной связи между 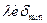 . Мера дисперсии
. Мера дисперсии 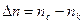 (с- синий, к- красный).
(с- синий, к- красный).
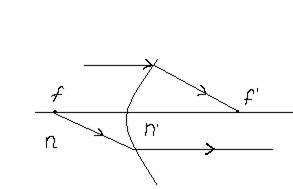
Отражение и преломление света на сферической поверхности раздела.
Будем рассматривать только те лучи, направление распространения которых с нормалью к поверхности составляет малые углы. Т.е. sin и tg можно заменить значениями углов (параксиальные лучи).
Введем прямоугольную систему координат с началом О на сферической поверхности. Тогда все расстояния, отчитываемые влево меньше О, а вправо больше О. Вертикальные отрезки отчитываемые вверх больше О, а вниз меньше О.
Углы меньше О если их sin меньше О.Если углы отчитываемые от нормали к сферической поверхности не совпадают с выбранной осью абсцисс, то больше нуля если поворот луча к нормали против часовой стрелки. 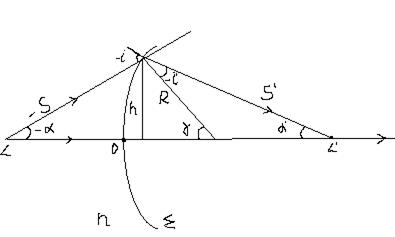
Рассмотрим преломление 2-х лучей: одного вдоль оси абсцисс и другого под углом ~ (-α). Первый луч не изменит направление. Второй падая под углом (-i)преломится под углом ~ (-i’). Причем для параксиальных лучей 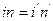 .
.
Так как i внешний в треугольнике, то 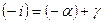 , т.е.
, т.е. 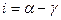
аналогично 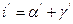 .
.
так как 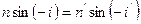 или
или 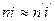 или
или 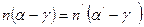
т.е. 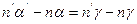 , но
, но 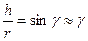 , отсюда
, отсюда 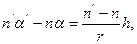
а так как 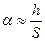 ;
; 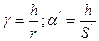 , то
, то 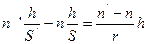 или
или 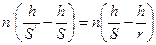
или же 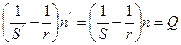 т.е. преломлении параксиальных лучей на сферической поверхности остается постоянной некоторая величина Q (инвариант Аббе).
т.е. преломлении параксиальных лучей на сферической поверхности остается постоянной некоторая величина Q (инвариант Аббе).
Преобразим полученное выражение:
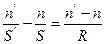 (*)
(*)
Если источник бесконечно далеко, т.е. 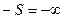 , то после преломления лучи собираются в точке называемой задним фокусом сферической поверхности
, то после преломления лучи собираются в точке называемой задним фокусом сферической поверхности 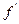 . Значение
. Значение 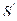 тогда
тогда 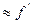 .
.
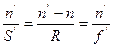

Если источник поместить в точку 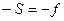 , т.е. в передний фокус сферической поверхности, то
, т.е. в передний фокус сферической поверхности, то 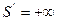 и лучи распространяются параллельно друг другу.
и лучи распространяются параллельно друг другу.
Причем 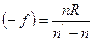 .
.
Величину, 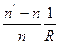 определяющую переднее фокусное расстояние называется оптической силой сферической поверхности.
определяющую переднее фокусное расстояние называется оптической силой сферической поверхности.
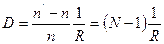 ; где
; где 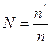
Если в (*) заменить n на 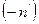 то получим формулу сферического зеркала
то получим формулу сферического зеркала
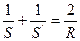 .
.
Величина 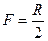 называется фокусным расстоянием зеркала. Если R>0, то
называется фокусным расстоянием зеркала. Если R>0, то 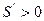 , т.е. изображение даваемое выпуклым зеркалом всегда мнимое.
, т.е. изображение даваемое выпуклым зеркалом всегда мнимое.
Если R>0, то 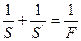 или,
или, 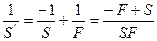 т.е.
т.е. 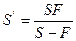 и в зависимости от значения S может быть как мнимое, так и действительным.
и в зависимости от значения S может быть как мнимое, так и действительным.
Если R→∞ , то 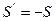 и следовательно изображение даваемое плоским зеркалом всегда мнимое.
и следовательно изображение даваемое плоским зеркалом всегда мнимое.
Лучи света, от источника конечных размеров пройдя через сферические поверхности раздела, могут дать стигматическое изображение предмета.
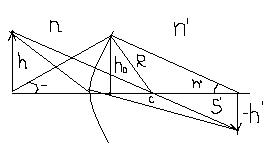
Линейное увлечение V есть отношение поперечного размера изображения 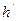 к поперечному размеру изображения h.
к поперечному размеру изображения h. 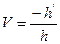

Угловым увеличением W называется отношение значения угла  под которым лучи сходятся в точку изображения , к значению угла и под которым соответствующие лучи выходят от источника.
под которым лучи сходятся в точку изображения , к значению угла и под которым соответствующие лучи выходят от источника.
Из подобия треугольников:
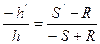 или
или 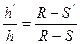 , но
, но 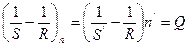 т.е.
т.е. 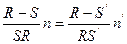 но
но 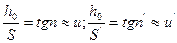 т.е.
т.е. 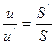 поэтому
поэтому 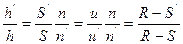 или nuh=
или nuh= 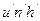 теорема Лагранжа- Гельмгольца т.е. произведение линейного увеличения
теорема Лагранжа- Гельмгольца т.е. произведение линейного увеличения 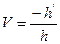 . Углового увеличения
. Углового увеличения 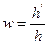 и отношение показателей преломления 2-х сред к
и отношение показателей преломления 2-х сред к 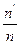 для сферической поверхности есть величина постоянная n=1:
для сферической поверхности есть величина постоянная n=1: 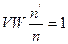

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|