Хелпикс

Главная

Контакты

Случайная статья



Вычисление длины дуги кривой, заданной в прямоугольных координатах

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒


Вычисление длины дуги кривой, заданной в прямоугольных координатах

Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.

Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).

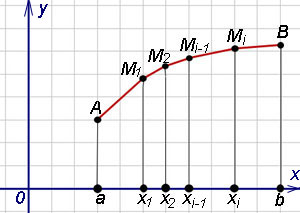
Возьмём на дуге AB точки A, M1, M2, ..., Mi, ..., B с абсциссами x0 = a, x1, x2, ..., xi, ..., b = xn и проведём хорды AM1, M1M2, ..., Mn-1B, длины которых обозначим соответственно через Δs1, Δs2, ..., Δsn. Тогда получим ломаную AM1M2 ... Mn-1B, вписанную в дугу AB. Длина ломаной равна

.

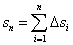Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:

.

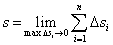Этот предел интегральной суммы равен определённому интегралу

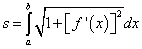(1).

Формула выше и есть формула для вычисления дуги кривой.

Пример 1.Найти длину дуги кривой 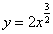, если .

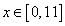Решение. Находим производную данной функции:

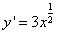
Используем формулу (1), подставляя найденную производную:

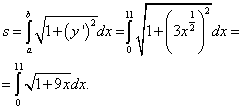
Производим подстановку:

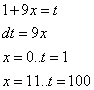
Далее находим:

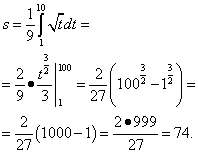
Ответ: длина дуги кривой равна 74.

Пример 2.Найти длину окружности .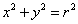

Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:

,

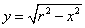откуда находим производную функции:

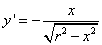
Используем формулу (1) подставляя в неё производную, получаем:

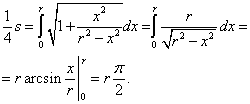
Ответ: длина всей окружности равна .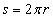

Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:

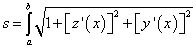. (2)


⇐ Предыдущая12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.