
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла
Пример 1.Найти площадь фигуры, ограниченной графиком функции 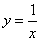 , осью абсцисс (Ox) и прямыми x = 1, x = 3.
, осью абсцисс (Ox) и прямыми x = 1, x = 3.
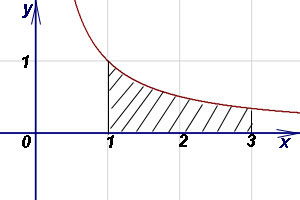
Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):
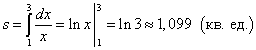 .
.
Пример 2.Найти площадь фигуры, ограниченной графиком функции 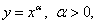 , прямой x = 1 и осью абсцисс (Ox).
, прямой x = 1 и осью абсцисс (Ox).
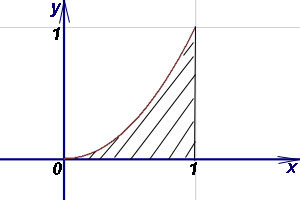
Решение. Результат применения формулы (1):
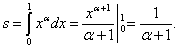
Если 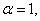 то s = 1/2; если
то s = 1/2; если 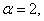 то s = 1/3, и т.д.
то s = 1/3, и т.д.
Пример 3.Найти площадь фигуры, ограниченной графиком функции 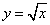 , осью абсцисс (Ox) и прямой x = 4.
, осью абсцисс (Ox) и прямой x = 4.
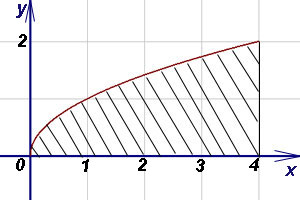
Решение. Фигура, соответствующая условию задачи - криволинейная трапеция, у которой левый отрезок выродился в точку. Пределами интегрирования служат 0 и 4. Поскольку 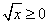 , по формуле (1) находим площадь криволинейной трапеции:
, по формуле (1) находим площадь криволинейной трапеции:
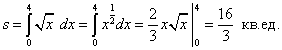 .
.
Пример 4.Найти площадь фигуры, ограниченной линиями 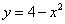 ,
, 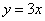 ,
, 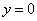 и находящейся в 1-й четверти.
и находящейся в 1-й четверти.
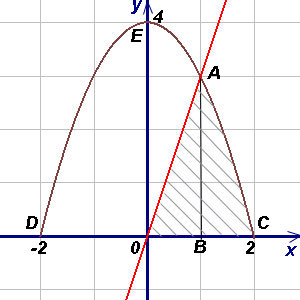
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры, заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной трапеции ABC. При вычислении площади треугольника OAB пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC - абсциссы точек A и C (A является точкой пересечения прямой OA и параболы, а C - точкой пересечения параболы с осью Ox). Решая совместно (как систему) уравнения прямой и параболы, получим 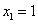 (абсциссу точки A) и
(абсциссу точки A) и 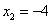 (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим
(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично получим 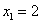 ,
, 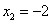 (абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
(абсциссы точек C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
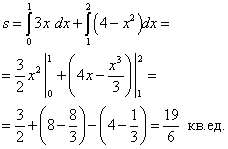
Пример 5.Найти площадь криволинейной трапеции ACDB, если уравнение кривой CD 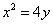 и абсциссы A и B соответственно 1 и 2.
и абсциссы A и B соответственно 1 и 2.
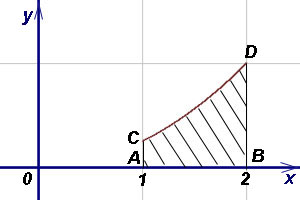
Решение. Выразим данное уравнение кривой через игрек: 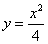 Площадь криволинейной трапеции находим по формуле (1):
Площадь криволинейной трапеции находим по формуле (1):
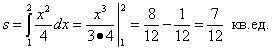 .
.
Пример 6.Найти площадь фигуры, ограниченной параболой 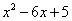 и осью абсцисс (Ox).
и осью абсцисс (Ox).
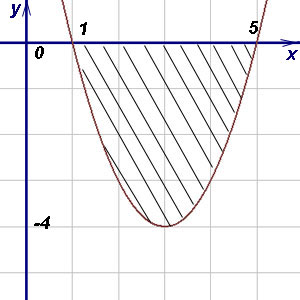
Решение. Данная фигура расположена ниже оси абсцисс. Поэтому для вычисления её площади воспользуемся формулой (2). Пределами интегрирования являются абсциссы 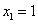 и
и 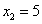 точек пересечения параболы с осью Ox. Следовательно,
точек пересечения параболы с осью Ox. Следовательно,
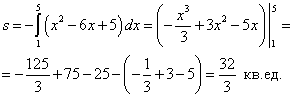
Пример 7.Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.
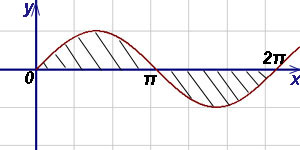
Решение. Площадь данной фигуры можем найти по формуле (2):
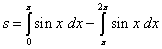 .
.
Найдём отдельно каждое слагаемое:
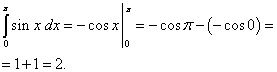 .
.
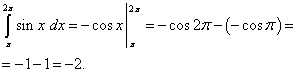 .
.
Окончательно находим площадь:
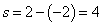 .
.
Пример 8.Найти площадь фигуры, заключённой между параболой 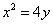 и кривой
и кривой 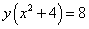 .
.
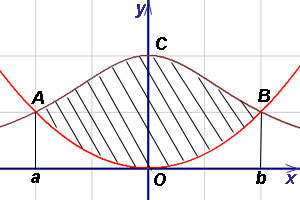
Решение. Выразим уравнения линий через игрек:
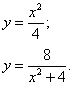
Площадь по формуле (2) получим как
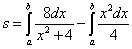 ,
,
где a и b - абсциссы точек A и B. Найдём их, решая совместно уравнения:
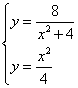
Отсюда
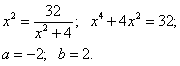
Окончательно находим площадь:
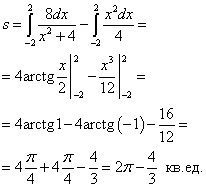
И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|