
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
й способ вычисления определенного интеграла-по формуле Ньютона-Лейбница
1-й способ вычисления определенного интеграла-по формуле Ньютона-Лейбница
Если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,
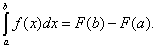 (38)
(38)
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
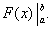
Поэтому формулу Ньютона-Лейбница будем записывать и так:
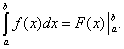 (39)
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
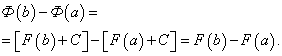
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разность F(b) - F(a). Полученное число и будет определённым интегралом..
При a = b по определению принимается
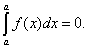
Пример 1.Вычислить определённый интеграл

Решение. Сначала найдём неопределённый интеграл:
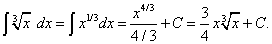
Применяя формулу Ньютона-Лейбница к первообразной
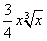
(при С = 0), получим
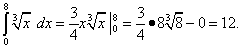
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2.Вычислить определённый интеграл
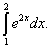
Решение. Используя формулу
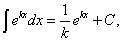
получим
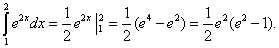
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|