
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
й способ -вычисление определённых интегралов методом интегрирования по частям
2-й способ -вычисление определённых интегралов методом интегрирования по частям
При выводе формулы интегрирования по частям в неопределенном интеграле было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b , получим
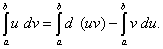
Первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
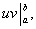
получаем формулу интегрирования по частям для вычисления определенного интеграла:
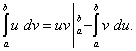 (**)
(**)
Пример 6.Вычислить определённый интеграл
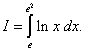
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (**) находим
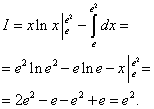
3-й способ вычисления определённого интеграла- метод замены переменной.
Пусть
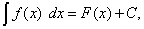
где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
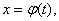
то в соответствии с формулой (16) можно записать
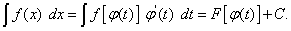
В этом выражении
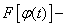
первообразная функция для
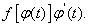
В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна
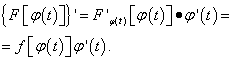
Пусть α и β – значения переменной t , при которых функция
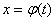
принимает соответственно значения a и b, т.е.
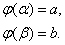
Тогда
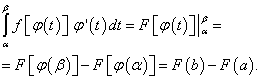
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть
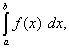
поскольку F(x) – первообразная для f(x).
Итак,
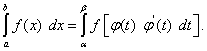 (50)
(50)
Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
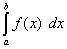
после замены переменной
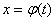
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами 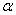 и
и 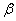 . Чтобы найти новые пределы, нужно в уравнение
. Чтобы найти новые пределы, нужно в уравнение
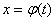
поставить значения x = aи x = b, т.е. решить уравнения
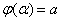
и
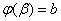
относительно 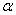 и
и 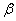 . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
. После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9.Вычислить определённый интеграл
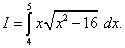
Решение. Произведём замену переменной, полагая
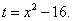
Тогда dt = 2x dx, откуда x dx = (1/2) dt, и подынтегральное выражение преобразуется так:
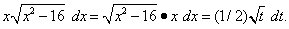
Найдём новые пределы интегрирования. Подстановка значений x = 4и x = 5в уравнение
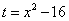
даёт
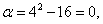
а
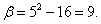
Используя теперь формулу (50), получим
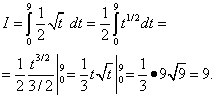
После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|