Лабораторная работа. Решение прямой и обратной задач магниторазведки для шара.

Лабораторная работа. Решение прямой и обратной задач магниторазведки для шара.

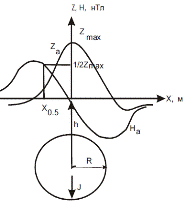
Геологические тела, имеющие форму шара, в природных условиях встретить трудно. Однако при приблизительных расстояниях от центра залежи до кромки тела по трем взаимно перпендикулярным осям х, у, z геологическое тело неправильной формы в достаточно удаленной точке наблюдения можно уподобить шару. Магнитные аномалии от реальных тел неправильной формы иногда похожи на аномалии от шара. Для профиля, проходящего через точку проекции центра шара на поверхность наблюдений, значения Z_a и H_a определяются по формулам:

;

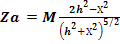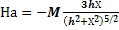
   где М = V·J = 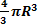·J - магнитный момент шара [A×m²]; h - глубина до центра шара (м); Х – расстояние от начала координат до точки наблюдения (м);   R – радиус шара (м);          V – объём шара (м³); J – намагниченность шара (А/м).

   Значения Z_a и H_a определяются в системе СИ в А/м и переводятся в гаммы (γ). 1А/м=10³СГС, 1А/м=4𝝅10³γ, 1Э=79,6А/м, 1Э=10⁵γ, 1нТл (единица магнитной индукции) для воздуха приблизительно равна 1γ (единица напряженности магнитного поля).

  Задание 1. Вычисление значений Z_a и H_a – компонент магнитного поля для вертикально намагниченного шара. (Прямая задача).

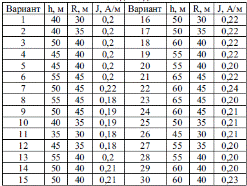
    По данным R, h, J, которые согласно заданному варианту, выбираются из таблицы 1, необходимо рассчитать значения Z_a и H_a в следующих точках профиля:0 м, ±5 м, ±10 м, ±20 м, ±40 м, ±60 м, ± 80м, ±100 м, ±200 м, ±400 м, ±800м. Вычисления производятся с точностью до целых единиц нТл и представляются в виде таблицы 2. Рассчитанные поля Z_a и H_a в гаммах необходимо перевести в нТл и изобразить в виде графиков вдоль профиля, откладывая по оси абсцисс расстояния точек наблюдений от эпицентра залежи, по оси ординат – значения поля.



  h (м) =               R (м) =                   J (А/м) =               V (м³) =                       М (А·м²) =

Z_a нТл H_a нТл

-400

-200

-100

…

-5

…

12 3 4 5 6 7 8 9 10 Следующая ⇒