
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Учебный элемент № 3. УЧЕБНЫЙ ЭЛЕМЕНТ № 4
Учебный элемент № 3
Цель: закрепить навыки решения логарифмических уравнений вида 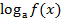 =
= 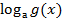
Рекомендации к выполнению:
Помните, что решение таких уравнений основано на том, что такое уравнение равносильно уравнению f(x) =g(x) при дополнительных условиях f(x) > 0 ,g(x) > 0.
Можно при решении таких уравнений использовать следующую схему:
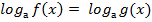
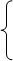 | |||
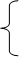 | |||
f(x) =g(x) f(x) = g (x)
f(x) > 0 или g(x) > 0
Внимательно разберите данные ниже решения и выполните задания самостоятельной работы.
Пример: Решите уравнения. 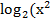 -3х + 1) =
-3х + 1) = 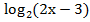
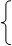 х2- 3х +1 = 2х -3,
х2- 3х +1 = 2х -3,
2х – 3 >0;
Решим уравнение х2 -3х + 1 = 2х – 3
х2 – 3х + 1 – 2х + 3 = 0
х2 - 5х +4 = 0
D= 25 -16 = 9
х1 = 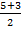 = 4, х2 =
= 4, х2 = 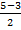 = 1
= 1
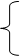 |
x = 4 или х = 1
x > 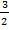
х = 4 Ответ: 4.
Пример: Решите уравнение lg(x2 +75) – lg (x -4) =2
Решение: lg(x2 +75) – lg(x-4) = 2
 Найдем ОДЗ : х2 +75 > 0
Найдем ОДЗ : х2 +75 > 0
x - 4 > 0
 |
x –любое число
х > 4 ОДЗ: (4; +∞)
lg(x2 +75)=2 + lg (х-4)
lg (x2 +75) = lg 100 +lg (x-4)
lg (x2 +75) = lg (100x – 400)
x2 +75 = 100x – 400
x2 -100x +75 +400 =0
x2 -100x +475 = 0
D = 1002 – 4 1 475 = 100 000 – 1900 = 8100
x1 = 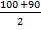 =95
=95
x2 = 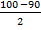 = 5 95 и 5 входят в ОДЗ
= 5 95 и 5 входят в ОДЗ
Ответ: 95; 5.
Выполните самостоятельную работу.
| I вариант | II вариант |
1. 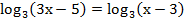 (2 б) (2 б)
| 1. 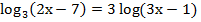 (2 б) (2 б)
|
| 2. lg(х2 -17) = lg (х+3) (3 б) | 2. 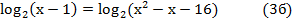
|
3. 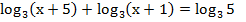 (4 б) (4 б)
| 3. lg(х+1) + lg(x-1) = lg32 (4б) |
УЧЕБНЫЙ ЭЛЕМЕНТ № 4
Цель: закрепить умения решать простейшие логарифмические неравенства.
Рекомендации к выполнению:
Решение логарифмических неравенств основано на том, что функция у = 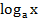 при а>1 является монотонно возрастающей на своей области определения, а при 0<a<1монотонно убывающей на своей области определения.
при а>1 является монотонно возрастающей на своей области определения, а при 0<a<1монотонно убывающей на своей области определения.
При переходе от простейшего неравенства к равносильным системам неравенств, не содержащих знака логарифма следует учитывать область допустимых значений исходного неравенства.
При решении логарифмических неравенств пользуйтесь следующей схемой:
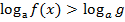 (x) (x)
a > 1 0 < a < 1
g(x) > 0 f(x) > 0
|
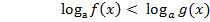
a> 1 0 < a < 1
f(x) > 0 g(x) > 0 |
Пример: 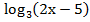 < 2
< 2
Решение: 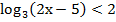
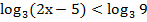
Функция у = 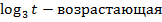
 2х-5< 9
2х-5< 9
2х-5 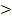 0;
0;
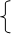 2х <14
2х <14
2х >5;
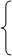 |
х <7
х>2,5 х 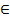 (2,5; 7)
(2,5; 7)
Ответ: х 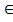 (2,5; 7)
(2,5; 7)
Выполните письменную самостоятельную работу.
| Iвариант | IIвариант |
1. 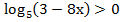 (1 б) (1 б)
| 1 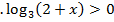 (1б) (1б)
|
2 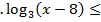 1 (1 б) 1 (1 б)
| 2 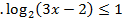 (1 б) (1 б)
|
3 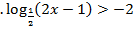 (1 б) (1 б)
| 3 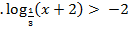 (1 б) (1 б)
|
| 4. lg (x2 +2x+2) < 1 (2 б) | 4. lg(x2 +x+4) < 1 (2 б) |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|


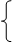
 f(x) > g(x) f(x) < g(x)
f(x) > g(x) f(x) < g(x)

 f(x) < g(x) f(x) > g(x)
f(x) < g(x) f(x) > g(x)