
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задания для самостоятельной работы
7) 4х-5ּ2х+4=0
Представим 4х как 22х, получим:
22х-5ּ2х+4=0
Введем подстановку: 2х обозначим переменной t. Cледовательно: 22х=t2. Получим:
t2-5t+4=0
Найдем корни уравнения по теореме Виета:
t1=1
t2=4
Заменим t на 2х:
2х=1
Заметим, что 20=1
2х=20
Приравняем показатели:
х=0
2х=4
Заметим, что 4=22
2х=22
Приравняем показатели:
х=2
Уравнение имеет два действительных корня 0 и 2.
Ответ: х = 0 и х = 2.
Примеры решения неравенств:
1) 45-2x<0,25.
Представим правую часть в виде: 0,25=(25/100)=(1/4)=4-1;
45-2x<4-1; функция у=4х с основанием 4>1 возрастает на R, в связи с этим, опуская основания степеней, знак неравенства сохраним:
5-2x<-1; — 2x<-1-5; — 2x<-6 |:(-2) при делении обеих частей неравенства на отрицательное число, знак неравенства меняют на противоположный: x>3.
Ответ: (3; +∞).
2) 0,42х+1≥0,16.
Представим число 0,16 в виде степени числа 0,4. Получаем: 0,42х+1≥0,42; основание степеней – число 0,4 — удовлетворяет условию: 0<0,4<1; в связи с этим, опускаем основания степеней, а знак неравенства меняем на противоположный:
2х+1≤2; 2х≤2-1; 2х≤1 |:2 x≤0,5.
Ответ: (-∞; 0,5].
3) 23-x+21-x>40. Применим формулу: ax+y=ax∙ay. Запишем неравенство в виде:
23∙2-x+21∙2-x>40; Вынесем общий множитель за скобки:
2-x∙(23+21)>40; упрощаем левую часть:
2-x∙(8+2)>40;
2-x∙10>40 |:10
2-x>4;
2-x>22; основание степени — число 2>1,значит, знак неравенства сохраняем:
— x>2 |:(-1) при делении обеих частей неравенства на отрицательное число — знак неравенства меняют на противоположный: x<-2.
Ответ: (-∞; -2).
Задания для самостоятельной работы
Решите уравнения:
* 1. 3х = 81.
* 2. 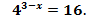
* 3. 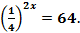
* 4. 
* 5. 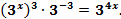
* 6. 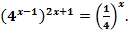
* 7. 2ּ3х+1 – 3х = 15.
* 8. 36х – 4 6х – 12 = 0.
Решите неравенства:
* 1. 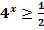 .
.
* 2. 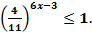
* 3. 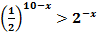 .
.
* 4. 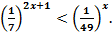
* 5. 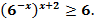
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|