Тройные интегралы

Тройные интегралы

Повторный интеграл в пространстве вводится аналогично повторному интегралу на плоскости.

Пусть функция 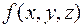непрерывна в правильной области 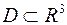, причём 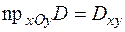– правильная область в :

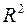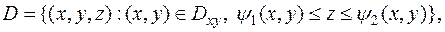
Зафиксируем точку 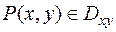и проинтегрируем непрерывную функцию 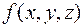–функцию одной переменной 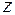! – по отрезку 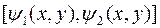. Очевидно, что полученный интеграл будет зависеть от координат точки :

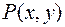Можно показать, что функция 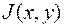– непрерывная. Следовательно, существует повторный интеграл от этой функции по области :

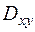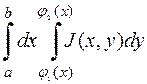
или, окончательно,

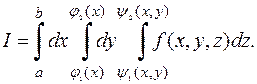(3)

Эта конструкция и называется повторным интегралом в 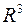. Ещё раз заметим, что вычисление такого интеграла производится справа налево! Избегайте грубых ошибок: в пределах интегрирования внутренних интегралов могут быть только внешние переменные.

Очевидно, что кроме рассмотренного порядка интегрирования (сначала по 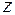, потом по 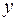и, наконец, по 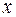) существуют и другие порядки, причём все они приводят к одному и тому же числу .

Пример. Расставить пределы интегрирования в повторном интеграле от функции 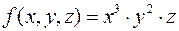по области ограниченной поверхностями , , , .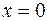

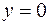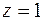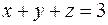Решение. Все указанные поверхности – это плоскост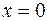и: и 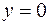– координатные, 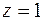– параллельна координатной . Вместе с четвёртой плоскостью они ограничивают некий тетраэдр. Его проекция на 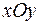– это треугольник ограниченный осями 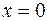, 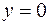и прямой, которая является проекцией линии пересечения гране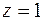й и 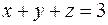. Исключая переменную 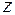из этих уравнений, получим уравнение проекции: .

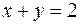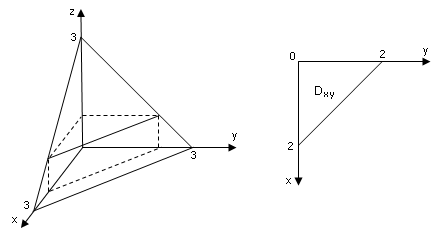
Рис.9

Итак, для точек области 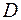имеем: 1) абсцисса 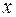изменяется от 0 до 2; 2) для каждого фиксированного 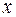ордината 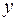изменяется от 0 до прямой 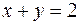, т.е. до 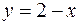; 3) аппликата 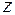изменяется от плоскости 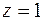до плоскости 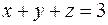, т.е. до 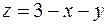. Стандартная запись области:

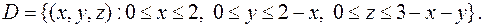
Повторный интеграл имеет вид:

Ещё раз напомним: вычисления производятся справа налево!

⇐ Предыдущая 1 2 345 Следующая ⇒