
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 3.Перейдя к полярным координатам, вычислить двойной интеграл , если D - I четверть круга .
Пример 3.Перейдя к полярным координатам, вычислить двойной интеграл , если D - I четверть круга .
Решение. Полагая х = r cosj, y = r sinj, имеем уравнение окружности
r2 cos2j + r2 sin2j = 1 или r = 1, тогда
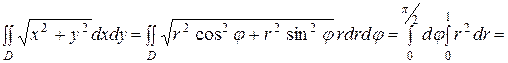 =
= 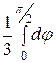 =
= 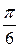 .
.
Приложения двойного интеграла
Вычисление площади плоской фигуры. Площадь плоской фигуры, ограниченной областью D, находится по формуле
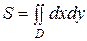 .
.
Если область D определена, например, неравенствами  , то
, то
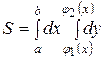 .
.
Если область D в полярных координатах определена неравенствами 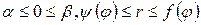 , то
, то
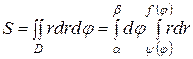 .
.
Пример 4.Вычислить площадь фигуры, ограниченной линиями
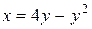 , x + y = 6.
, x + y = 6.
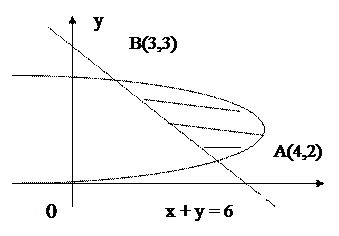
Рис.4
Решение. Построим данную область Д: 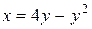 , x + y = 6 (рис.16). Найдем координаты точек пересечения заданных линий, решая систему уравнений:
, x + y = 6 (рис.16). Найдем координаты точек пересечения заданных линий, решая систему уравнений: 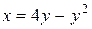 и
и
x + y = 6. В результате получим А(4;2), В(3;3). Таким образом,
D= 
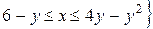 и площадь области равна:
и площадь области равна:
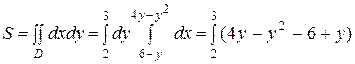 dy =
dy = 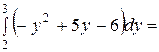
= 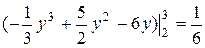 (кв.ед.).
(кв.ед.).
Вычисление объёмов тел
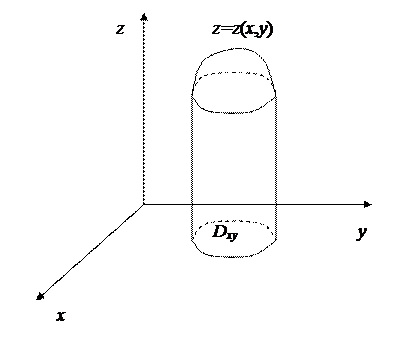
А. Объём цилиндрического тела
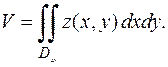
Отметим, что кроме этой формулы можно написать ещё две аналогичные. Речь идёт о случаях, когда “основание” тела лежит в плоскости 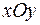 или
или 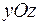 , а “крыша” задаётся, соответственно, неотрицательной функцией
, а “крыша” задаётся, соответственно, неотрицательной функцией 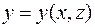 или
или 
Рис.5.
Пример 5. Вычислить объём тела, ограниченного поверхностями 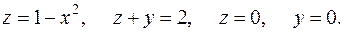
| |
|
|
| |
| |
| |
|
|
|
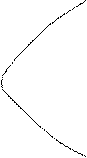





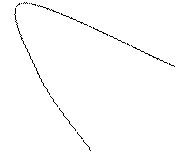







 Решение.Поверхность
Решение.Поверхность 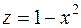 – это цилиндрическая поверхность, образующие которой параллельны оси ординат (переменной
– это цилиндрическая поверхность, образующие которой параллельны оси ординат (переменной  нет в уравнении
нет в уравнении
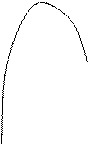 |
Рис.6.
а направляющей служит парабола 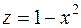 в плоскости
в плоскости 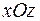 . Поверхности
. Поверхности 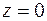 и
и 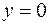 – координатные плоскости
– координатные плоскости 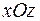 и
и 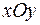 соответственно, а
соответственно, а 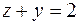 – плоскость, параллельная оси
– плоскость, параллельная оси 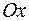 . Проекция тела
. Проекция тела  на плоскость
на плоскость 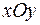 , т.е. его “основание” – это прямоугольник
, т.е. его “основание” – это прямоугольник  . Однако, над одной его частью “крышей” служит плоскость
. Однако, над одной его частью “крышей” служит плоскость 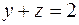 , а над другой частью “крыша” – это параболический цилиндр
, а над другой частью “крыша” – это параболический цилиндр 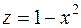 . Поэтому, при сведении двойного интеграла к повторному необходимо разбить
. Поэтому, при сведении двойного интеграла к повторному необходимо разбить 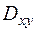 на две части.
на две части.
Лучше спроектировать тело на плоскость 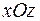 . В этой плоскости “основание” данного тела – это параболический сегмент
. В этой плоскости “основание” данного тела – это параболический сегмент 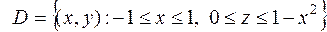 . “Крышей” в этом случае служит плоскость
. “Крышей” в этом случае служит плоскость 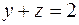 , т.е.
, т.е. 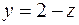 .
.
 Итак, имеем для объёма (рис.6)
Итак, имеем для объёма (рис.6)
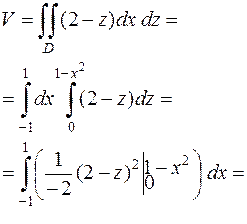

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|