
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вычисление массы полоской фигуры
Вычисление массы полоской фигуры
Рассмотрим в плоскости 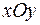 материальную пластину, т.е. некоторую область
материальную пластину, т.е. некоторую область 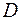 , в которой распределено некое вещество с поверхностной плотностью
, в которой распределено некое вещество с поверхностной плотностью 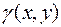 . Тогда, как известно (см. § 1, IV), масса всей пластины есть двойной интеграл по
. Тогда, как известно (см. § 1, IV), масса всей пластины есть двойной интеграл по 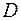 от
от 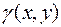 :
:
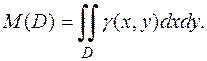
Один из примеров вычисления массы приведён в § 3. Рассмотрим ещё один характерный пример.
Пример Вычислить массу прямоугольного равнобедренного тре-угольника с гипотенузой 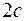 . Известно, что плотность
. Известно, что плотность 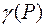 в любой точке
в любой точке 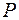 треугольника пропорциональна расстоянию от
треугольника пропорциональна расстоянию от 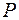 до гипотенузы, а в вершине прямого угла равна
до гипотенузы, а в вершине прямого угла равна  .
.
|
 .
.
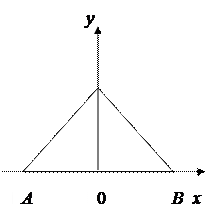
Уравнения катетов: 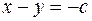 (левый) и
(левый) и
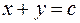 (правый). Таким образом, область можно записать так:
(правый). Таким образом, область можно записать так:
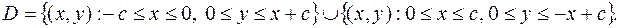
Рис.8
Лучше, однако, записать область иначе:

Далее, по условию 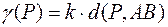 , т.е.
, т.е. 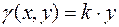 . Коэффициент пропорциональности находим из условия
. Коэффициент пропорциональности находим из условия
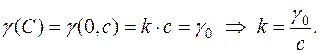
Итак, для искомой массы имеем:
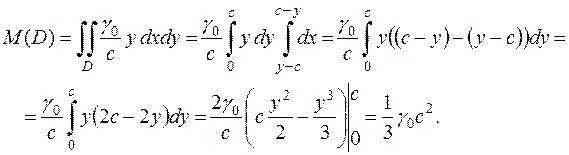
Отметим, что размерность полученного ответа – это размерность массы.
Итак, для искомой массы имеем:

Отметим, что размерность полученного ответа – это размерность массы.
Вычисление координат центра масс пластины
Известно из физики, что, если масса распределена дискретно в отдельных 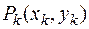 точках, то координаты
точках, то координаты  центра масс такой системы материальных точек вычисляются по формулам
центра масс такой системы материальных точек вычисляются по формулам
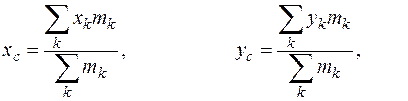
в которых  – масса, сосредоточенная в точке
– масса, сосредоточенная в точке 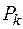 .
.
Пусть теперь в плоской области 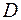 имеем непрерывное распределение массы с поверхностной плотностью
имеем непрерывное распределение массы с поверхностной плотностью 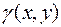 . Чтобы найти координаты центра масс такой области, поступим обычным образом. Разобьём область
. Чтобы найти координаты центра масс такой области, поступим обычным образом. Разобьём область 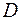 на отдельные части
на отдельные части  и выберем точки
и выберем точки 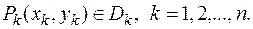 Масса
Масса 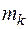 , распределенная в
, распределенная в 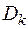 , приближенно равна
, приближенно равна 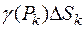 , где
, где 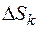 – площадь области
– площадь области 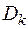 . Если считать, что вся масса
. Если считать, что вся масса  сосредоточена в точке
сосредоточена в точке 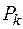 , то придём к дискретному распределению массы, и поэтому
, то придём к дискретному распределению массы, и поэтому
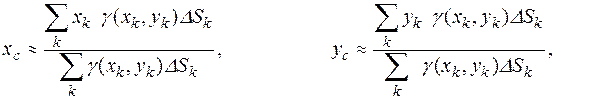
Чтобы получить точные значения для 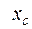 и
и 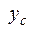 , необходим переход к пределу при
, необходим переход к пределу при 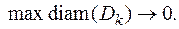
Но три суммы в написанных выше формулах – это интегральные суммы и в пределе дадут интегралы:
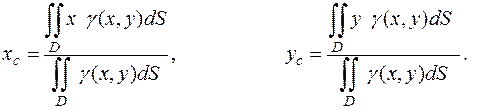
Интегралы, стоящие в числителях этих формул, называют статическими моментами области 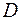 относительно осей
относительно осей 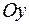 и
и 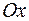 соответственно.
соответственно.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|