
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Кратные интегралы. Двойные интегралы
Кратные интегралы
Двойные интегралы
Пусть функция f(x,y) определена в ограниченной замкнутой области D плоскости хОy. Разобьём область D произвольном образом на n элементарных областей, имеющих площадь ∆σ 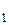 , ∆σ
, ∆σ 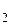 , …, ∆σ
, …, ∆σ 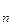 и диаметры d
и диаметры d 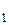 , d2, … , d
, d2, … , d 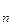 (диаметром области называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку P
(диаметром области называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку P 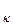 (ξ
(ξ 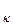 ;ηк ) и умножим значение функции в точки P
;ηк ) и умножим значение функции в точки P 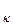 на площадь этой области.
на площадь этой области.
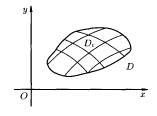
Рис.1
Интегральной суммой для функции f(x,y) по области D называется сумма вида
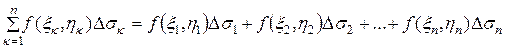 .
.
Если при max d 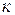
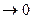 интегральная сумма имеет определенный конечный предел
интегральная сумма имеет определенный конечный предел
I = 
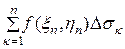 ,
,
не зависящий от способа разбиения D на элементарные области и от выбора точек P 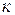 в пределах каждой из них, то этот предел называется двойным интегралом от функции f( x, y ) в области D и обозначается следующим образом:
в пределах каждой из них, то этот предел называется двойным интегралом от функции f( x, y ) в области D и обозначается следующим образом:
I = 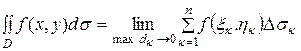 .
.
Если f(x,y)>0 в области D, то двойной интеграл 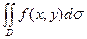 равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x,y), сбоку цилиндрической поверхностью с образующими, параллельными оси О
равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x,y), сбоку цилиндрической поверхностью с образующими, параллельными оси О 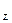 , и снизу областью D плоскости хОy.
, и снизу областью D плоскости хОy.
Основные свойства двойного интеграла:
1. 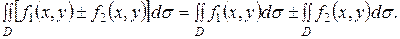
2. 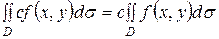 , где с – постоянная.
, где с – постоянная.
3. Если область интегрирования D разбита на две области D 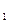 и D
и D 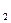 , то
, то
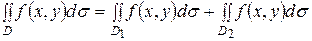
4. Оценка двойного интеграла. Если m ≤ f(x,y) ≤ M, то 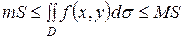 , где S - площадь области D, а m и M – соответственно наименьшее и наибольшее значения функции f(x,y)в области D.
, где S - площадь области D, а m и M – соответственно наименьшее и наибольшее значения функции f(x,y)в области D.
Пример 1.Вычислить 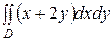 ,если область D ограничена прямыми y = х, y = 2х, х =2, х =3.
,если область D ограничена прямыми y = х, y = 2х, х =2, х =3.
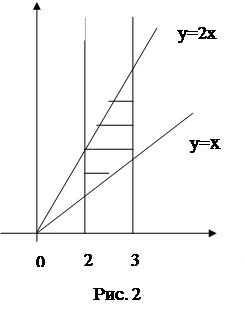
Решение. Вначале построим заданную область D (рис.2). Как видно
из графика D = 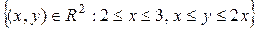 .
.
Тогда
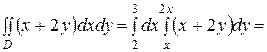
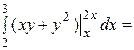
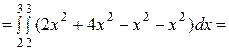
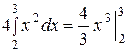 = 25
= 25 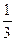 .
.
Пример 2.Изменить порядок интегрирования в интеграле:
I 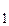 =
= 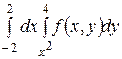 .
.
Решение. Вначале по пределам интегрирования определяем область интегрирования. Полагая xравным пределам интеграла с переменной х, а y равным пределам интеграла с переменной y, получим уравнения линий, ограничивающих эту область: х = -2, х = 2, y = 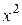 , y = 4.
, y = 4.
Построив эти линии, получим параболический сегмент ОАВ, симметричный оси О 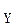 (рис.3).
(рис.3).
Интегрируем в другом порядке – вначале по х, затем по y. Пределы внутреннего интеграла находим, разрешая относительно х
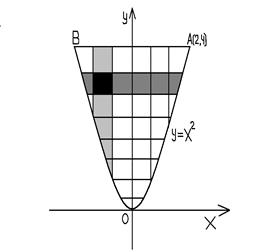 уравнение параболы х = -
уравнение параболы х = - 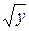 и х =
и х = 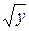 . Пределы внешнего интеграла y = 0 и х = 4 находим как наименьшее и наибольшее значение y во всей области ОАВ. Следовательно,
. Пределы внешнего интеграла y = 0 и х = 4 находим как наименьшее и наибольшее значение y во всей области ОАВ. Следовательно,
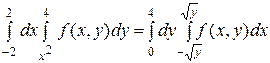 .
.
Рис. 3
Двойной интеграл в полярных координатах.Преобразование двойного интеграла от прямоугольных координат х, y к полярным координатам ρ, θ, связанным с прямоугольными координатами соотношениями
х = r cosj, y = r sinj,
осуществляется по формуле
|
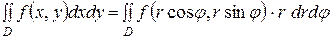 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|