
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 1.. Решение.. Пример 2.. Решение.. Пример 3.. Решение.
Пример 1.
Вычислить массу прямолинейного стержня АВ, если линейная плотность в каждой его точкевычисляется по закону 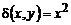 ,
, 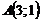 ,
, 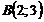 .
.
Решение.
Масса участка кривой определяется криволинейным интегралом 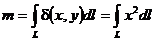 , где
, где 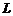 - отрезок прямой АВ.
- отрезок прямой АВ.
Запишем уравнение прямой АВ в каноническом виде.
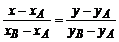 ,
, 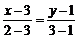 ,
, 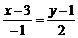 .
.
Упрощая это уравнение, получим 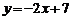 , где
, где 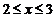 . Поскольку
. Поскольку 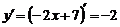 , сведем криволинейный интеграл к определенному интегралу, используя формулу (3).
, сведем криволинейный интеграл к определенному интегралу, используя формулу (3).
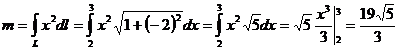 .
.
Пример 2.
Вычислить статический момент относительно начала координат однородного участка кривой 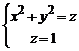 .
.
Решение.
Статический момент кривой относительно оси 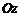 определяется по формуле (см. Приложение):
определяется по формуле (см. Приложение):
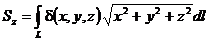 .
.
Поскольку кривая однородная, то плотность 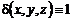 . Тогда
. Тогда
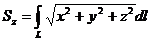 .
.
Уравнение кривой 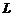
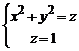 можно преобразовать к виду
можно преобразовать к виду
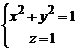 .
.
Полученная система задает окружность с радиусом 1, лежащую в плоскости 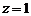 . Используя параметрические уравнения окружности, запишем уравнения кривой
. Используя параметрические уравнения окружности, запишем уравнения кривой 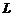 в параметрическом виде.
в параметрическом виде.
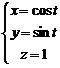 ,
, 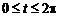 .
.
Вычислим криволинейный интеграл по формуле (1), учитывая равенства: 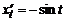 ,
, 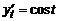 ,
, 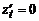 ,
, 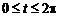 .
.
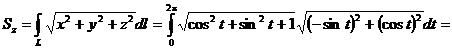
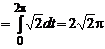 .
.
Пример 3.
Вычислить массу кривой 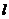 , если плотность
, если плотность 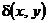 в каждой точке равна расстоянию от нее до начала координат, а кривая
в каждой точке равна расстоянию от нее до начала координат, а кривая 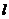 задана уравнением:
задана уравнением: 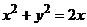 .
.
Решение.
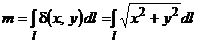 .
.
Приведем уравнение кривой к каноническому виду
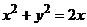 ,
, 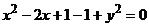 ,
, 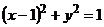 .
.
Это уравнение окружности с центром в точке 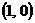 и радиусом
и радиусом 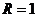 (рис. 1).
(рис. 1).
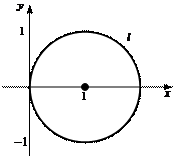
Рис. 1.
Перейдём к полярным координатам:
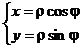 .
.
Уравнение кривой в полярных координатах имеет вид:
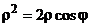 или
или 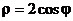 , где
, где 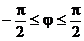 .
.
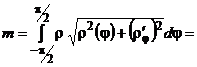
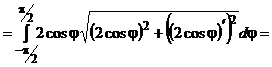
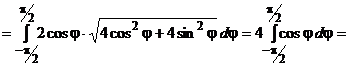
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|