Контакты

Случайная статья

Приложения криволинейных интегралов

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Длина дуги 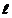плоской или пространственной линии 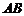определяется формулой

.

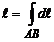Если 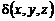– линейная плотность вещества в точках дуги, то масса дуги 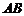определяется формулой

.

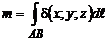Координаты центра тяжест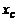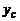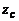и , , дуги 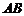находятся из соотношений

, ,

.

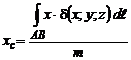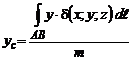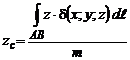Статические моменты 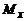и 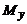плоской дуги 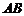относительно координатных осей Ох и Оу определяются формулами

, ,

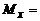
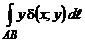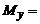
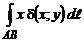где 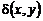– линейная плотность вещества в точках плоской дуги.

Моменты инерции 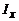, 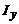плоской дуги 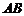относительно координатных осей Ох и Оу определяются формулами

, .

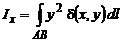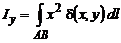Полярный момент инерции 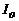плоской дуги 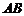относительно начала координат О определяется по формуле

.

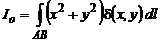Площадь 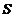фигуры, расположенной в плоскости Оху и ограниченной замкнутой линией L вычисляется по формуле

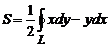. (7)

Работа 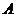векторного поля

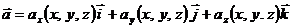
вдоль линии 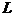от точки 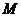до точки 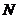находится через криволинейный интеграл второго рода по дуге 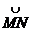кривой :

.

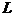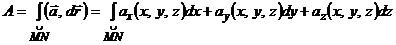Если векторное поле 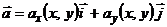плоское, то криволинейный интеграл второго рода вдоль кривой 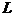, расположенной в координатной плоскости 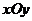, имеет вид

.

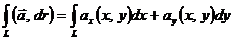Если кривая 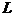задана параметрическими уравнениями: 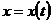; ; 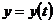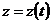, и функции 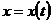; ; 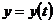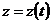- дифференцируемы, причём начальной точке 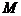соответствует значение параметра 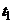, а конечной точке 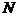- значение параметра 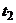, то

.

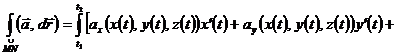
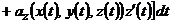Замечание.

1. Для однородных линий 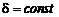и для простоты мы будем считать .

⇐ Предыдущая 123 4 Следующая ⇒

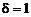© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.