
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАБОЧАЯ ТЕТРАДЬ ПО ТЕМЕ 6.2. Баранова Е.С.. Справочный материал. Вычисление криволинейного интеграла I рода. Вычисление криволинейного интеграла II рода
РАБОЧАЯ ТЕТРАДЬ ПО ТЕМЕ 6. 2
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Баранова Е. С.
Санкт-Петербург
Справочный материал
Вычисление криволинейного интеграла I рода
В зависимости от способа задания кривой, криволинейный интеграл первого рода сводится к определенному интегралу по следующим формулам.
Если пространственная кривая 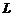 задана параметрическими уравнениями
задана параметрическими уравнениями 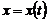 ;
; 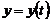 ;
; 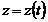 ;
; 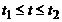 , то
, то
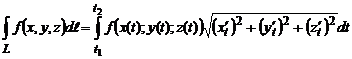 .
.
В частности, для плоской кривой 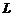 :
: 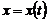 ;
; 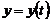 ;
; 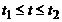
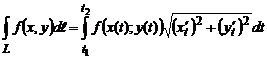 .
.
Если плоская кривая 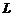 определена уравнением
определена уравнением 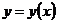 ;
; 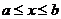 , то
, то
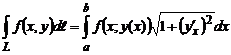 .
.
Если кривая 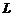 задана полярным уравнением
задана полярным уравнением 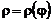 ;
; 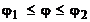 , то
, то
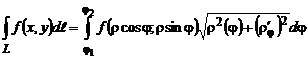 .
.
Вычисление криволинейного интеграла II рода
Если пространственная кривая 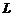 задана параметрическими уравнениями
задана параметрическими уравнениями 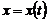 ;
; 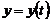 ;
; 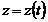 ;
; 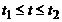 , причём перемещение от точки
, причём перемещение от точки 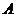 к точке
к точке 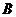 происходит при изменении параметра
происходит при изменении параметра 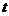 от
от 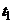 до
до 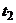 , то
, то
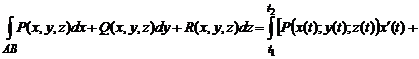
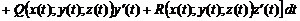 .
.
В частном случае для плоской кривой 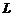 :
: 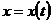 ,
, 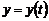 , причём перемещение от точки
, причём перемещение от точки 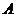 к точке
к точке 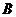 происходит при изменении параметра
происходит при изменении параметра 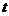 от
от 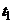 до
до 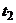 , криволинейный интеграл вычисляется по формуле
, криволинейный интеграл вычисляется по формуле
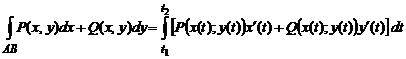 .
.
Если плоская кривая 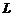 определена уравнением
определена уравнением 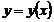 ; причём перемещение от точки А к точке В происходит при изменении
; причём перемещение от точки А к точке В происходит при изменении 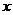 от
от 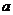 до
до 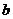 , то
, то
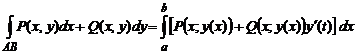 .
.
Замечание. При изменении направления интегрирования криволинейный интеграл II рода меняет свой знак:
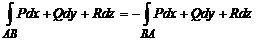 .
.
Сказанное верно и для замкнутой кривой, при этом выбор точки начала обхода безразличен. И положительным направлением обхода считается то, при котором область, ограниченная этой кривой, остаётся слева (для плоской кривой – это движение против часовой стрелки.

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|