Параболоиды.. Цилиндры.

Параболоиды.

Эллиптическим параболоидом называется поверхность с каноническим уравнением

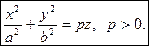
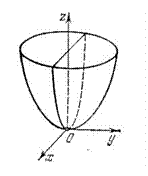Поверхность расположена в области 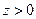. Сечениями в плоскостях 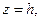являются эллипсы, а в плоскостях 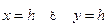– параболы, в плоскости 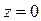– точка (0, 0, 0).

Гиперболическим параболоидом называется поверхность с каноническим уравнением

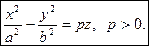
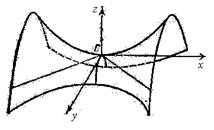
Применение метода сечений приводит к тому, что в плоскостях 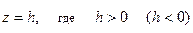обнаруживаются гиперболы, а в плоскостях 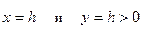– параболы, в плоскости 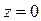– пересекающиеся прямые.

Конус.

Коническая поверхность – множество прямых (образующих) пространства, соединяющих все точки некоторой линии (направляющей) с данной точкой (вершиной) пространства. Каноническое уравнение конуса второго порядка имеет вид:

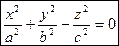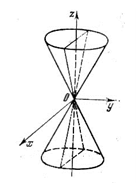Метод сечений позволяет составить представление о форме этой поверхности:

Осью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ. Поперечные сечения плоскостями 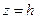являются эллипсами, а в плоскостях XOZ и YOZ - пересекающиеся прямые, проходящие через начало координат, сечения плоскостями 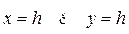– гиперболы, сечения плоскостями, не параллельными координатным, может дать параболу.

Цилиндры.

Цилиндрическая поверхность – множество прямых (образующих) пространства, параллельных заданному направлению и проходящих через некоторую линию (направляющую).

Эллиптический цилиндр задается каноническим уравнением

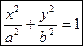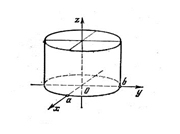Осью цилиндра является координатная ось OZ, поперечные сечения – эллипсы.

Гиперболический цилиндр задается каноническим уравнением

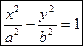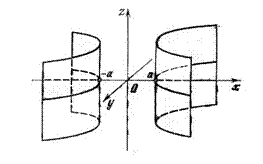Параболический цилиндр задается каноническим уравнением

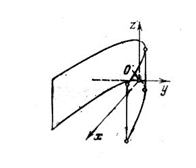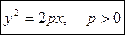
Заметим, что признаком рассмотренных цилиндрических поверхностей является отсутствие той переменнойв каноническом уравнении, которой

параллельна образующая.

⇐ Предыдущая 1 2 34