Эллипсоид.

Эллипсоидом называется поверхность второго порядка с каноническим уравнением

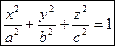Рассмотрим сечение эллипсоида плоскостью 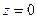. Линия пересечения эллипсоида и плоскости задается системой уравнений

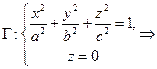
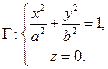
Г – эллипс с полуосями а и b в плоскости .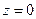

Рассмотрим сечение эллипсоида плоскостью 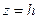. Линия пересечения задается системой уравнений

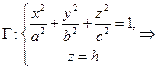
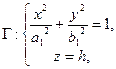
где 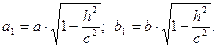Таким образом, если 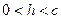, то Г – эллипс с полуосями 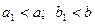в плоскост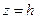и Если ,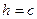
Г – точка с координатам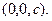и Если 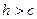, система решений не имеет, т. е. исследуемая поверхность не имеет общих точек с рассматриваемой плоскостью.

Далее, так как переменная z содержится в уравнении во второй степени, плоскость 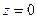является плоскостью симметрии эллипсоида. Отсюда следует, что достаточно исследовать форму поверхности и построить ее часть в области 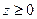, достроив затем остальную часть путем зеркального отражения найденного фрагмента поверхности относительно координатной плоскости ОXY.

Аналогично рассматриваются сечения поверхности плоскостями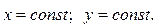

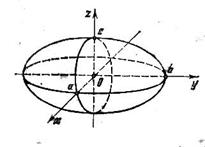
Эллипсоид - замкнутая овальная поверхность, имеющая три плоскости симметрии: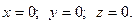

Если 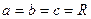, каноническое уравнение принимает вид

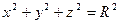
и задает сферу с центром в начале координат и радиусом R.

⇐ Предыдущая 123 4 Следующая ⇒