Контакты

Случайная статья

iL(t - t0) = iLпр+ A ( (t - t0) + )

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

iL(t - t0) = iLпр+ A ( (t - t0) + )

Принужденную составляющую найдем в схеме после коммутации:

Рисунок 5

По первому закону Кирхгофа:

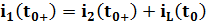
По второму закону Кирхгофа:

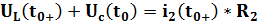
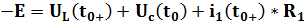
Откуда:

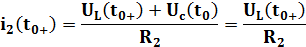
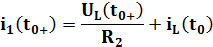
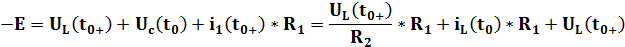
Отсюда легко выразить :

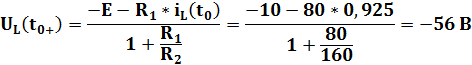
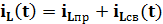
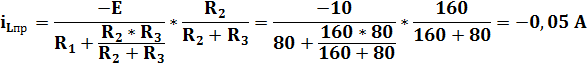
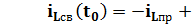= 0, 925 + 0, 05 = 0, 93 A

Постоянные интегрирования найдем из следующих условий:

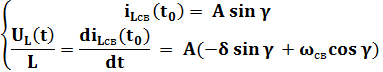
iLсв(t0) = A = 0, 93

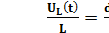= A*(- sin + cos ) = A*(-16898, 148*sin +

+4805, 68*cos ) = = - 3, 111*10⁴

Где = Re(p)= - 16898, 148

= Im(p) = 4805, 68

Выразив из первого уравнения А и подставив во второе, найдем

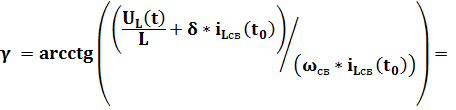
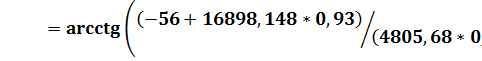= 163, 812⁰

Зная , определяем А:

А = 3, 336

Запишем окончательный результат:

iL(t - t0) = iLпр+ A ( (t - t0) + )

iL(t - t0) = -0, 05 + 3, 336* sin(4805, 68 (t - t0) + 163, 8120) A

t₀, как мы помним, определяется следующим образом:

t0 = 3 0 = =1. 012*10-4 c

Операторный метод:

Преобразуем схему с помощью эквивалентных замен:

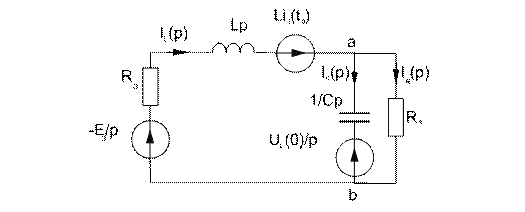
Рисунок 6

Полагаем потенциал узла = 0, тогда будет определяться по формуле для двух узлов:

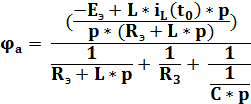
Подставляем известные значения и упрощаем:

=

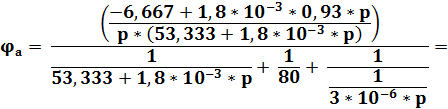
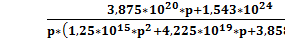
Проверим вычисления с помощью MathCAD:

Приложение MathCAD 2

Воспользуемся теоремой разложения и получим закон изменения напряжения на конденсаторе после коммутации:

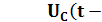4 + 50, 6* 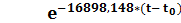(4805, 68*(t - t₀) + 185, 466⁰) B

Ток определяется следующей формулой:

=

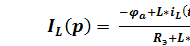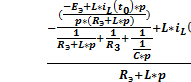
Подставим известные данные:

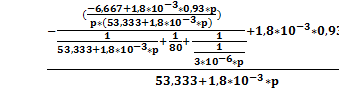
Упрощаем:

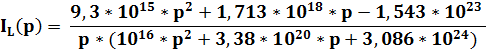
Найдем оригинал тока, используя теорему разложения:

Чтобы определить оригинал, необходимо вычислить корни знаменателя:

Найдем p_{1, 2} из уравнения:

B₁(p) = 0,

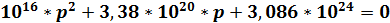
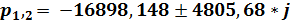
Проверим вычисления с помощью MathCAD:

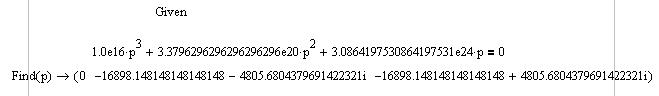
Приложение MathCAD 3

Найдем вспомогательные величины:

,

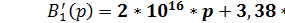A(0) = ,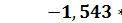

B₁(0) =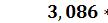

Затем, используем следующие формулы:

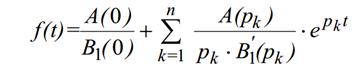
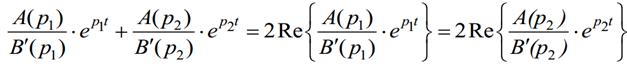
После подстановки получим:

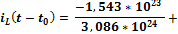
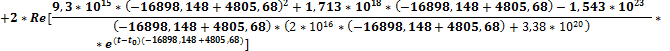
Подсчитав, данное выражение, получим:

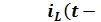-0, 05 + 2*Re(|0, 479 + 1, 609*j|*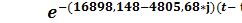

⇐ Предыдущая 1 234 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.