iL(0) = iLсв(0) + iLпр(0) = iLпр(0) + A

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

= 1235*t – 0, 042 A

i_L (t) =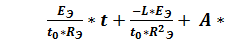

Находим независимое начальное условие (в схеме до коммутации):

Независимым начальным условием является ток через катушку индуктивности, имеем:

i_L(0)=0 А, т. к. до коммутации в цепи не действует источник ЭДС.

Находим константу интегрирования:

i_L (t) =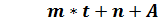

iL(0) = iLсв(0) + iLпр(0) = iLпр(0) + A

iL(0) = A + n = 0

Отсюда:

A = - n = = = 0, 042

Записываем конечный результат:

iL(t) = A

i_L(t₀) =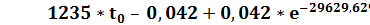

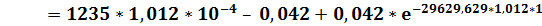0, 925 A

Определим ток i_L(t) методом интеграла Дюамеля:

Записываем, в каком виде должна быть представлена искомая величина:

iL(t) = e(0)*h(t) - A

Переходная характеристика имеет вид:

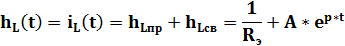
Найдем характеристический корень:

Входное сопротивление: :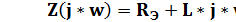

Характеристическое уравнение: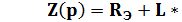

Отсюда: p = =

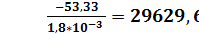
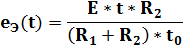
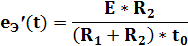
В момент времени t = 0:

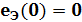
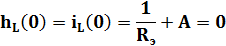
Отсюда:

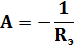
Тогда :

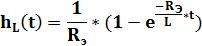
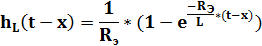
Интеграл Дюамеля для данного случая имеет вид:

i_L(t) = e_Э(0)*h(t) – =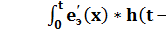

=

=

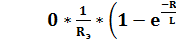
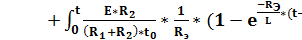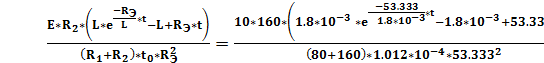
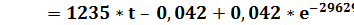А.

Как видно из полученного выражения, расчеты были проведены верно, т. к. результат сошелся с результатом, полученным классическим методом.

ЗАДАНИЕ 2

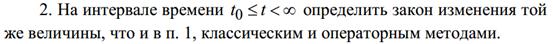
Выполнение задания:

Классический метод:

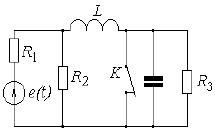
Рисунок 4

Сначала найдем характеристический корень.

Для этого разрываем цепь относительно любых зажимов и приравниваем входное сопротивление к нулю:

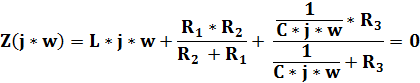
Составим характеристическое уравнение заменой j*w→ p:

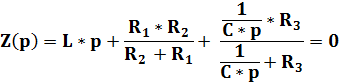
Отсюда, при подстановке известных величин находим p_{1, 2}:

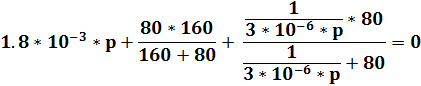
Отсюда p = - 16898, 148 4805, 68*j c^-1

Проверка расчета с помощью MathCAD:

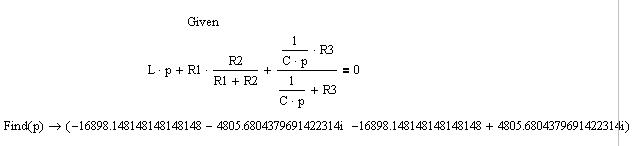
Приложение MathCAD 1

Искомая величина должна быть записана в виде:

⇐ Предыдущая 123 4 Следующая ⇒