
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОТВЕТ: а) , б) или , в) , г) ед
ОТВЕТ: а), б) или, в), г) ед
д) 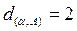 , е)
, е) 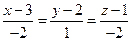 или
или 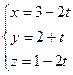 , ж)
, ж) 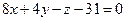 ,
,
з) 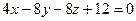
7.
А)
 1.
1. 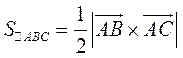
 2. Найдём координаты векторов
2. Найдём координаты векторов  :
: 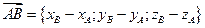

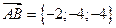
 3. Найдём координаты вектора
3. Найдём координаты вектора 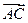 :
: 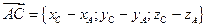
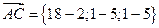
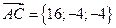
4. 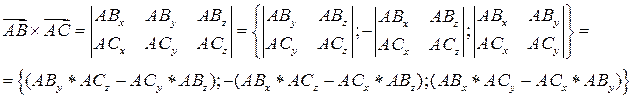
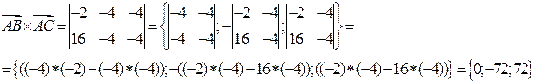
5. 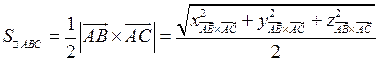
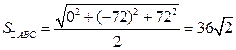 кв. ед
кв. ед
Б)
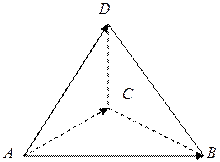 1.
1. 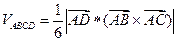 .
.
2. Найдём координаты векторов  :
: 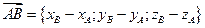
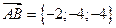
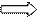 3. Найдём координаты вектора
3. Найдём координаты вектора 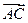 :
: 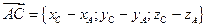
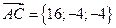
4. Найдём координаты вектора  :
: 
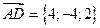
5. I 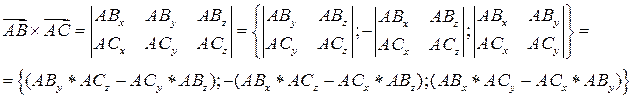
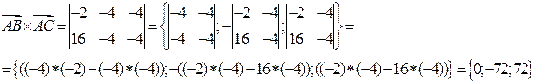

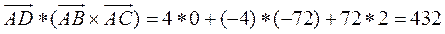
II.
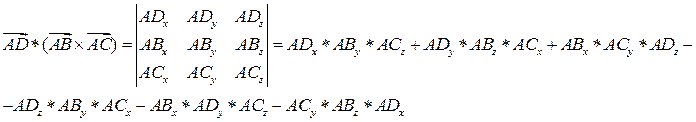
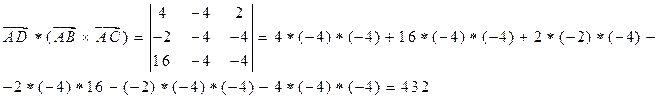
6. 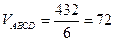 куб. ед.
куб. ед.
В)
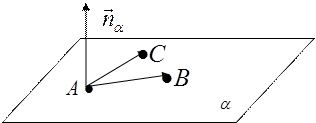 1. Для решения задачи воспользуемся тем, что вектор нормали плоскости
1. Для решения задачи воспользуемся тем, что вектор нормали плоскости 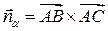 , перпендикулярен к искомой плоскости
, перпендикулярен к искомой плоскости 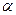 .
.
2. Найдём координаты вектора  :
: 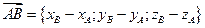 ,
, 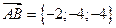 .
.
3. Найдём координаты вектора 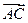 :
: 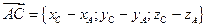 ,
, 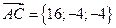
4. 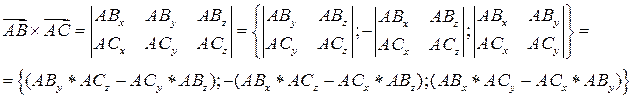
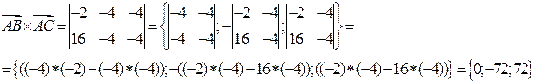
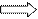


 5. .
5. . 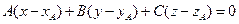 - уравнение искомой плоскости по заданной точке А и вектору нормали плоскости
- уравнение искомой плоскости по заданной точке А и вектору нормали плоскости 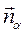 , где
, где 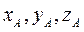 координаты точки А; A, B, C координаты вектора нормали
координаты точки А; A, B, C координаты вектора нормали 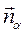 .
. 
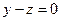
Частный случай расположения плоскости в пространстве A=D=0, следовательно плоскость проходит через ось Ох.
Г) 1. 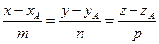 - общий вид уравнения прямой
- общий вид уравнения прямой 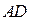 в пространстве, где
в пространстве, где 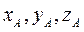 координаты точки А; m, n, p координаты направляющего вектора
координаты точки А; m, n, p координаты направляющего вектора 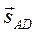 .
.
2. 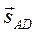 - направляющий вектор прямой
- направляющий вектор прямой 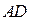 , следовательно, координаты вектора
, следовательно, координаты вектора 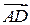 равны координатам вектора
равны координатам вектора 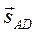 .
.
3. Найдём координаты вектора 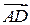 :
: 
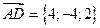
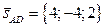
4. Тогда уравнение из пункта 1 можно переписать как: 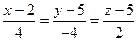
5. Запишем уравнение прямой AD в параметрической форме 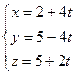 .
.
ОТВЕТ: а) 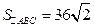 кв. ед., б)
кв. ед., б) 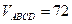 куб. ед.,
куб. ед.,
в) 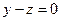 , г)
, г) 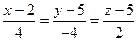 или
или 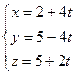
8.
а) 1. 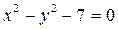 ,
, 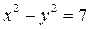 ,
, 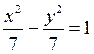
2. 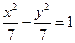 - уравнение гиперболы т к. в каноническом виде уравнение кривой второго порядка можно записать:
- уравнение гиперболы т к. в каноническом виде уравнение кривой второго порядка можно записать: 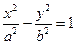
 3. 1. Координаты вершины гиперболы:
3. 1. Координаты вершины гиперболы: 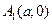 ,
, 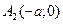 , где
, где  - действительная полуось гиперболы.
- действительная полуось гиперболы. 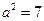
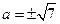 ,
, 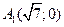 ,
, 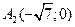
 3. 2. Фокусы гиперболы:
3. 2. Фокусы гиперболы: 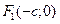 ,
,  , где
, где  ,
,  - действительная полуось гиперболы,
- действительная полуось гиперболы, 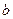 - мнимая полуось симметрии.
- мнимая полуось симметрии. 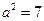 ,
, 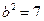 ,
, 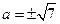 ,
, 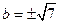
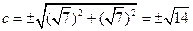
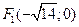 ,
, 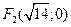

 3. 3. Асимптоты гиперболы
3. 3. Асимптоты гиперболы 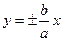 :
: 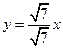
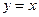 ;
; 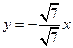
 .
.
 Директрисы гиперболы
Директрисы гиперболы  ,
, 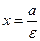 , где
, где 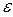 - эксцентриситет
- эксцентриситет  ,
, 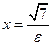 .
.
 Эксцентриситет гиперболы
Эксцентриситет гиперболы 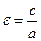 ,
, 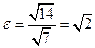 ,
,
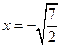
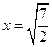
Б) 1. 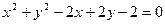
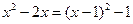
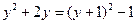 ,
, 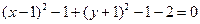 ,
, 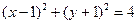
2. 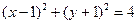 - уравнение окружности т. к. в каноническом виде уравнение кривой второго порядка можно записать
- уравнение окружности т. к. в каноническом виде уравнение кривой второго порядка можно записать  , где
, где 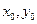 - координаты точки О - центра окружности, а R – радиус окружности.
- координаты точки О - центра окружности, а R – радиус окружности.
3. Тогда из  и
и 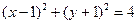 координаты точки О (1; -1), R=2 (из
координаты точки О (1; -1), R=2 (из 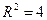 )
)
В) 1. 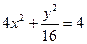 ,
, 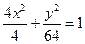 ,
, 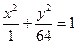 .
.
2. 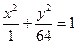 - уравнение эллипса т. к. в каноническом виде уравнение кривой второго порядка можно записать:
- уравнение эллипса т. к. в каноническом виде уравнение кривой второго порядка можно записать: 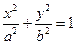
3. Вершины эллипса 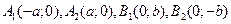 , где
, где  - большая полуось,
- большая полуось, 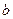 - малая полуось:
- малая полуось:
 Из уравнения
Из уравнения 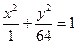
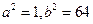
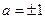 ,
, 
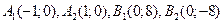 ,
, 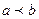 эллипс вытянут вдоль оси оy.
эллипс вытянут вдоль оси оy.
 Фокусы эллипса
Фокусы эллипса 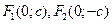 , где
, где 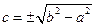 :
: 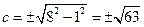
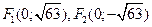
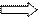 Директрисы эллипса
Директрисы эллипса 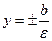 , где
, где 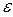 - эксцентриситет
- эксцентриситет 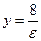 ,
, 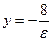 .
.
 Эксцентриситет эллипса
Эксцентриситет эллипса 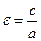 :
: 
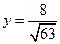 ,
, 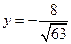
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|