
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Санкт-Петербургский университет Государственной противопожарной службы МЧС России
Санкт-Петербургский университет Государственной противопожарной службы МЧС России
Кафедра высшей математики и системного моделирования сложных процессов
Проверил
доцент кафедры
ВМиСМСП,
к. п. н., доцент
Т. А. Селеменева
Оценка_______
«__» __ 2021 г.
Расчетно-графическая работа
по дисциплине: «Высшая математика»
тема: «Элементы линейной алгебры и аналитической геометрии»
Вариант №7
Выполнил
курсант/студент гр. ЭЭ-17
Дяковский Павел
Николаевич
«01» декабря 2020г.
_________
(подпись)
Санкт-Петербург
ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ №1
ЧАСТЬ 1 " Элементы линейной алгебры и аналитической геометрии"
Вариант 7.
1. Даны матрицы А и В. Найти А× В, В× А, 2АТ - В.
А =  ; В =
; В = 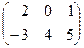 .
.
2. Решить систему уравнений А× Х=В: а) методом Гаусса; б) по формулам Крамера; в) матричным методом.
А = 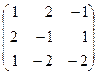 ; В =
; В = 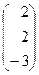 .
.
3. Найти ранг матрицы.
А = 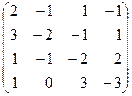
4. Даны векторы 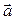 ;
; 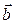 ;
; 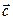 . Найти: скалярное произведение векторов
. Найти: скалярное произведение векторов 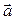 и
и 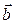 и угол между ними; проекцию вектора
и угол между ними; проекцию вектора 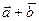 на направление вектора
на направление вектора 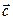 ; векторное произведение векторов
; векторное произведение векторов 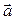 и
и 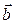 и площадь параллелограмма, построенного на этих векторах; смешанное произведение векторов
и площадь параллелограмма, построенного на этих векторах; смешанное произведение векторов 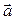 ,
, 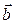 ,
, 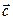 .
.
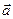 = (2, 2, -3);
= (2, 2, -3); 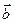 = (1, -2, 0);
= (1, -2, 0); 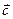 = (-3, 4, 0).
= (-3, 4, 0).
5. Даны вершины А, В, С треугольника. Найти: уравнение и длину медианы AM; уравнение и длину высоты АD; угол А треугольника АВС.
A(-1, 3); B(4, 3); C(1, 1).
6. Даны: точка А, уравнения прямой и плоскости. Найти: а) угол между прямой и плоскостью; б) уравнение прямой, проходящей через точку А перпендикулярно данной плоскости; в) уравнение плоскости, проходящей через точку А перпендикулярно прямой; г) расстояние от точки до прямой; д) расстояние от точки до плоскости; е) уравнение прямой, проходящей через точку A параллельно данной прямой; ж) уравнение плоскости, проходящей через точку А параллельно данной плоскости; з) уравнение плоскости, проходящей через точку А параллельно данной прямой.
A(3, 2, 1); 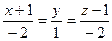 ;
; 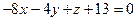 .
.
7. Даны точки А, В, С, D. Найти: а) площадь треугольника АВС; б) объем пирамиды АВСD; в) уравнение плоскости АВС; г) уравнение прямой АD.
A(2, 5, 5); B(0, 1, 1); C(18, 1, 1); D(6, 1, 7).
8. Привести уравнения кривых второго порядка к каноническому виду. Определить тип кривой. Найти координаты вершин и фокусов; сделать чертеж.
а) 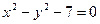 ; б)
; б) 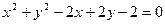 ;
;
в) 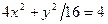
Решение:
1. A =  ; В =
; В = 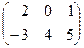 .
.
А× В
A*B=C; А= [3x2], B= [2x3]; C= [3x 2]*[2 x3] = [3x3] => матрицы А и В сцепленные и их можно перемножать.
C = 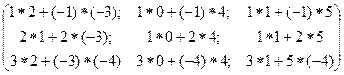 =
= 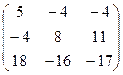
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|