
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
В×А. ОТВЕТ: Rg A=2. ОТВЕТ: , , , , кв.ед, .
В× А
B*A=C; B= [2x3], А= [3x2]; C= [2x3]*[3x2] = [2x2] => матрицы B и A сцепленные и их можно перемножать.
C = 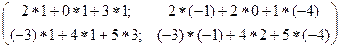 =
= 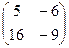
2АТ - В
A =  ;
; 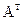 =
= 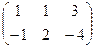 ;
; 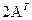 =
= 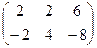
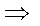
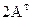 - B =
- B = 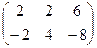 -
- 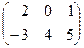 =
= 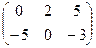
ОТВЕТ: А× В = 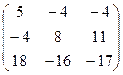 ; В× А =
; В× А = 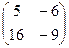 ; 2АТ - В =
; 2АТ - В = 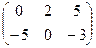
2. а) А =  ; В =
; В = 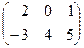 А× Х=В, где
А× Х=В, где 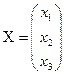
1. Запишем систему в развёрнутом виде:
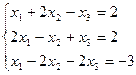
2. Запишем расширенную матрицу A*: A* = 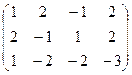
3. Сведём расширенную матрицу к ступенчатому виду (прямой ход метода Гаусса):
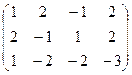
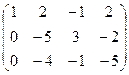
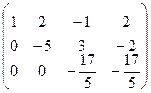

 4. RgA=RgA*=3 система имеет решения. 5. d=n-r, n=3, r=3, d=3-3=0
4. RgA=RgA*=3 система имеет решения. 5. d=n-r, n=3, r=3, d=3-3=0
есть 1 решение. 6. Запишем ступенчатую систему, разрешённую в координатной форме:
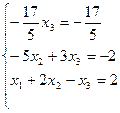 7. Найдём неизвестные
7. Найдём неизвестные 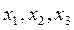


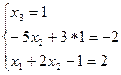
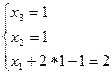
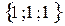
8. Проверка
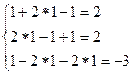 Ответ:
Ответ: 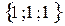
б) 1. А= 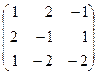 ; В =
; В = 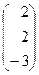 , А× Х=В, где
, А× Х=В, где 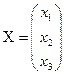
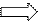 detA=
detA= 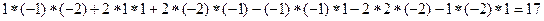
2. Система имеет размер 3х3 (nxn); detA=17 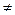 0 система имеет единственное решение.
0 система имеет единственное решение.
3. Воспользуемся формулой Крамера 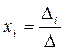 , где
, где 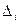 - определитель, полученный из
- определитель, полученный из 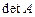 путём замены в нём
путём замены в нём 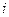 -го столбца столбцом свободных членов;
-го столбца столбцом свободных членов; 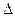 - определитель основной матрицы. Тогда
- определитель основной матрицы. Тогда 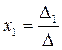 ,
, 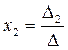 ,
, 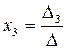 .
.
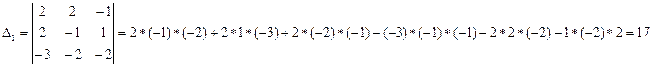
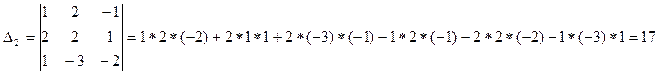
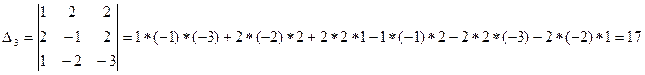
 4.
4. 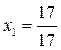 ,
, 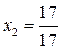 ,
, 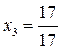
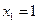 ,
, 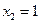 ,
, 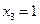
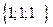
5. Запишем систему в развёрнутом виде:
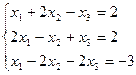 6. Проверка
6. Проверка 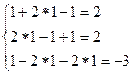 Ответ:
Ответ: 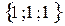
в) 1. А= 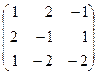 ; В =
; В = 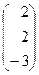 , А× Х=В, где
, А× Х=В, где 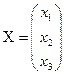
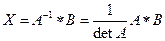
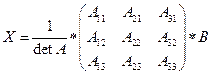
detA= 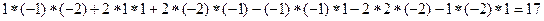
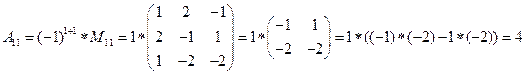
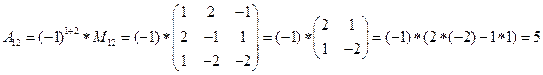
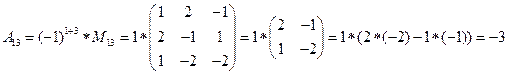
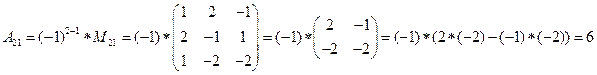
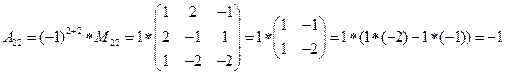
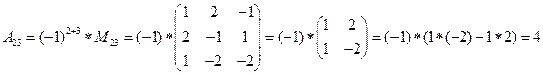
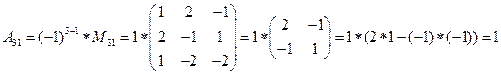
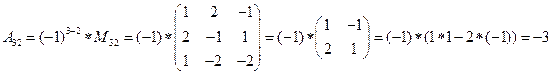
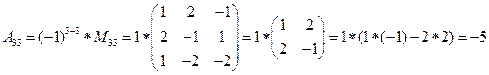
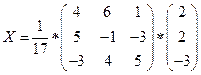
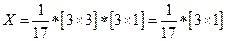

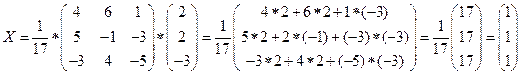

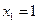 ,
, 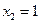 ,
, 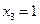 Ответ:
Ответ: 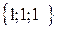
ОТВЕТ: 
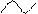
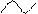
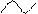 3. А=
3. А= 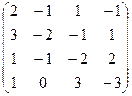
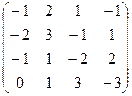
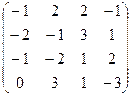
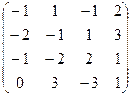
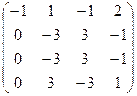

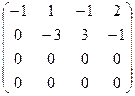 Rg A=2
Rg A=2
ОТВЕТ: Rg A=2
4. 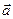 = (2, 2, -3);
= (2, 2, -3); 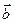 = (1, -2, 0);
= (1, -2, 0); 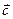 = (-3, 4, 0).
= (-3, 4, 0).
1. 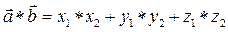
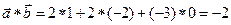
2. 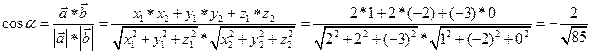
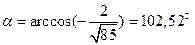
3. 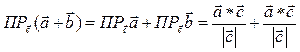 ,
,
где 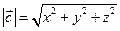 ,
, 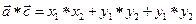
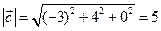
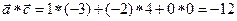
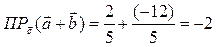
4. 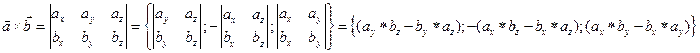
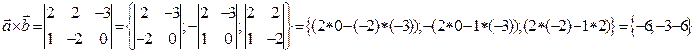 5.
5. 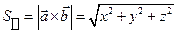 ,
, 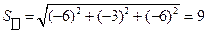 кв. ед.
кв. ед.
6. 1. 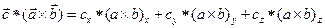 ,
, 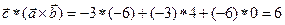
2. 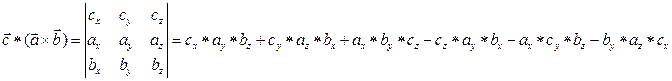
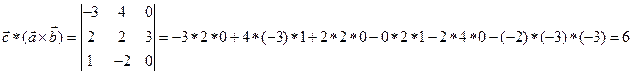
ОТВЕТ: , , , , кв. ед, .
5. Дано: А (-1; 3), В (4; 3) С (1; 1), АD – высота, АМ - медиана.
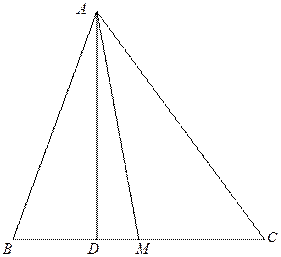 Найти: а) (АМ),
Найти: а) (АМ), 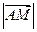 б) (АD),
б) (АD), 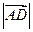
 Решение: А) 1.
Решение: А) 1. 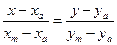 - уравнение прямой проходящей через 2 различные точки на плоскости, где
- уравнение прямой проходящей через 2 различные точки на плоскости, где 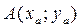 ,
, 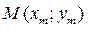 .
. 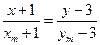 .
.


 2. Найдём координаты точки
2. Найдём координаты точки 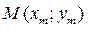 . Медиана АМ делит сторону ВС пополам (по определению). Точка М середина отрезка ВС, тогда координаты точки М найдём по формуле:
. Медиана АМ делит сторону ВС пополам (по определению). Точка М середина отрезка ВС, тогда координаты точки М найдём по формуле: 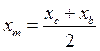 ,
, 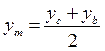
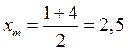 ,
, 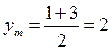
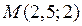 , тогда формулу из пункта 2 можно переписать
, тогда формулу из пункта 2 можно переписать 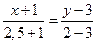
-(x+1)=3, 5(y-3)
-x-3, 5y+9, 5=0
x+3, 5y-9, 5=0 – уравнение прямой АМ.
 3.
3. 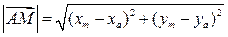
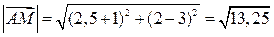 ед.
ед.
Б) 1. 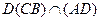 (
( 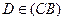 и
и 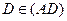 ),
), 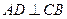 , тогда напишем уравнения прямых СВ и AD.
, тогда напишем уравнения прямых СВ и AD.

 2. (СВ):
2. (СВ): 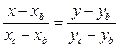 ,
, 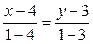
-2(х-4)=-3(у-3)
-2х+3у-1=0
2х-3у+1=0 – уравнение прямой СВ.
3. Используя условие перпендикулярности прямых на плоскости:


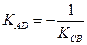 (где
(где 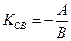 , где
, где 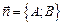 (Ах+Ву+С=0) – общее уравнение прямой) из уравнения прямой СВ.
(Ах+Ву+С=0) – общее уравнение прямой) из уравнения прямой СВ. 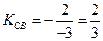
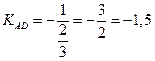
4. Тогда запишем уравнение прямой AD по заданной точке и угловому коэффициенту 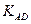 :
:

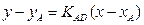
у-3=-1, 5(х+1)
1, 5х+у-1, 5=0 – уравнение прямой AD.
 5.
5. 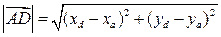 , где
, где 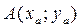 ,
, 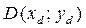
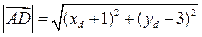 , найдём координаты точки D.
, найдём координаты точки D.
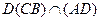 из этого следует, что необходимо решить СЛАУ:
из этого следует, что необходимо решить СЛАУ:

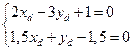
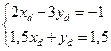 Решаем СЛАУ методом Крамера:
Решаем СЛАУ методом Крамера:
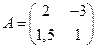 ,
, 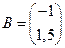 ,
, 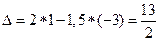
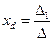 ,
, 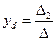
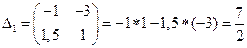 ,
, 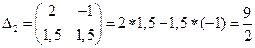


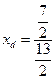
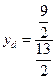
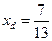
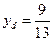
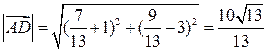 ед.
ед.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|