
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОТВЕТ: (AM): x+3,5y-9,5=0, ед., (AD): 1,5х+у-1,5=0, ед..
6. А)
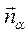

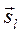

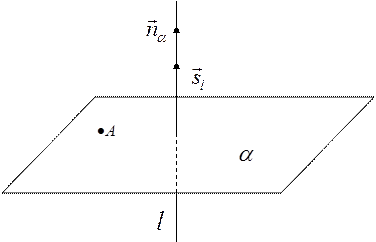
 1. Углом между прямой и плоскостью называется угол между прямой и её проекцией на эту плоскость.
1. Углом между прямой и плоскостью называется угол между прямой и её проекцией на эту плоскость.
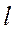
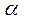
 2. Проведём направляющий вектор
2. Проведём направляющий вектор 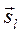 , и вектор нормали плоскости
, и вектор нормали плоскости 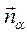 , тогда угол
, тогда угол 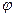 можно выразить:
можно выразить: 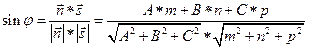 , где A, B, C координаты вектора нормали
, где A, B, C координаты вектора нормали 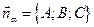 ; m, n, p координаты направляющего вектора
; m, n, p координаты направляющего вектора 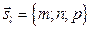 .
.
 3.
3. 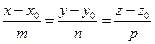 - общий вид уравнения прямой в пространстве,
- общий вид уравнения прямой в пространстве, 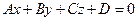 - общий вид уравнения плоскости. Тогда из
- общий вид уравнения плоскости. Тогда из 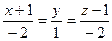 и
и 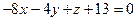 координаты вектора
координаты вектора 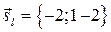 , а координаты вектора
, а координаты вектора 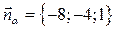

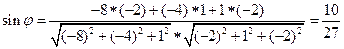
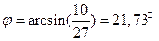
Б)
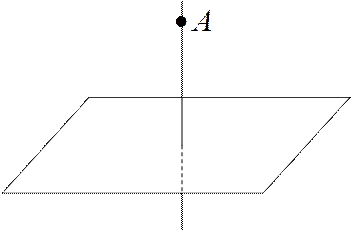 1. Если
1. Если 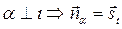
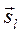


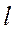
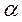 2.
2. 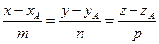 - общий вид уравнения прямой в пространстве, где
- общий вид уравнения прямой в пространстве, где 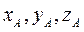 координаты точки А; m, n, p координаты направляющего вектора
координаты точки А; m, n, p координаты направляющего вектора 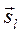 ,
, 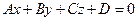 - общий вид уравнения плоскости где A, B, C координаты вектора нормали
- общий вид уравнения плоскости где A, B, C координаты вектора нормали 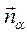 .
.
3. Тогда из 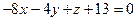 координаты
координаты 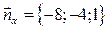
 4. Из пункта 1 следует, что
4. Из пункта 1 следует, что 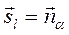 координаты направляющего вектора
координаты направляющего вектора 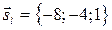
5. Тогда уравнение 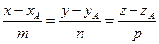 можно записать:
можно записать: 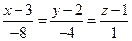
6. Перепишем уравнение из пункта 5 в параметрическую форму: 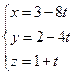
В)
 1.
1. 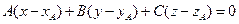 -уравнение искомой плоскости по заданной точке А и вектору нормали плоскости
-уравнение искомой плоскости по заданной точке А и вектору нормали плоскости 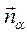 , где
, где 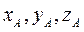 координаты точки А; A, B, C координаты вектора нормали
координаты точки А; A, B, C координаты вектора нормали 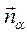 .
.
 2. Если
2. Если 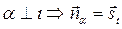 ,
, 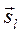 - направляющий вектор прямой заданной уравнением
- направляющий вектор прямой заданной уравнением 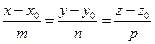 , где m, n, p координаты
, где m, n, p координаты 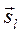 , из
, из 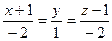 координаты направляющего вектора
координаты направляющего вектора 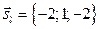 , но
, но 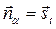 , значит координаты вектора нормали
, значит координаты вектора нормали 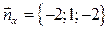 .
.
 3. Тогда уравнение из пункта 1 можно переписать:
3. Тогда уравнение из пункта 1 можно переписать: 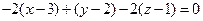
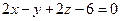
Г)
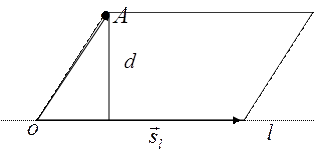 1. Прямая
1. Прямая 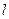 задана уравнением
задана уравнением 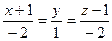 .
.  - канонический вид уравнения прямой, где
- канонический вид уравнения прямой, где 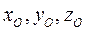 координаты точки О; m, n, p координаты направляющего вектора
координаты точки О; m, n, p координаты направляющего вектора 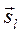
2. Тогда координаты точки 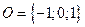 , а координаты направляющего вектора
, а координаты направляющего вектора 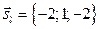 .
.
3. Расстояние d от точки А до прямой  можно найти через площадь параллелограмма, построенного на векторах
можно найти через площадь параллелограмма, построенного на векторах  и
и  :
: 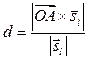
 4. Найдём координаты вектора
4. Найдём координаты вектора 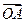 :
: 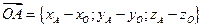
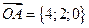 .
.
5. Найдём векторное произведение векторов 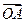 и
и  :
:
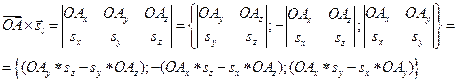
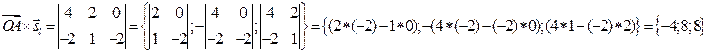
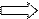 6. Найдём длину направляющего вектора
6. Найдём длину направляющего вектора  :
: 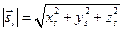
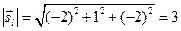
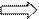 7. Найдём длину
7. Найдём длину 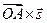 :
: 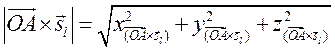
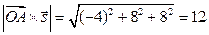 8.
8. 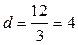 ед.
ед.
Д)

1. Расстоянием от точки до плоскости называется перпендикуляр проведённый из этой точки на плоскость; проведём перпендикуляр d из точки А на плоскость d – расстояние от точки А до плоскости 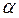 .
.
2. Расстояние от точки до плоскости можно найти по формуле: 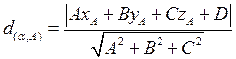 , где A, B, C координаты вектора нормали
, где A, B, C координаты вектора нормали 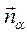 плоскости, D – свободный коэффициент;
плоскости, D – свободный коэффициент; 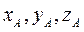 координаты точки А.
координаты точки А.
 3. Плоскость задана уравнением
3. Плоскость задана уравнением 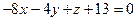
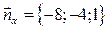 , D=13
, D=13
4. 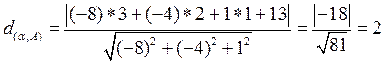 ед.
ед.
Е)
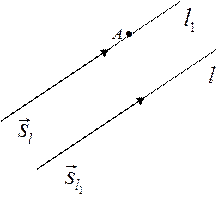 1. Запишем уравнение прямой
1. Запишем уравнение прямой  в общем виде
в общем виде  , где m, n, p координаты направляющего вектора
, где m, n, p координаты направляющего вектора 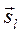 .
.
2. Тогда уравнение прямой 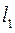 проходящей через точку А запишем как: .
проходящей через точку А запишем как: . 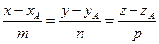 , где
, где 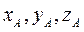 координаты точки А; m, n, p координаты направляющего вектора
координаты точки А; m, n, p координаты направляющего вектора 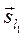 .
.
 3.
3. 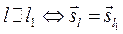 , т. к.
, т. к. 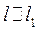 - по условию, то
- по условию, то 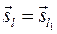 координаты этих векторов тоже равны.
координаты этих векторов тоже равны.
 4. Из
4. Из 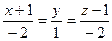 координаты направляющего вектора
координаты направляющего вектора 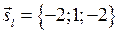 координаты направляющего вектора
координаты направляющего вектора 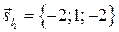 что уравнение прямо проходящей через точку А параллельно данной прямой можно записать:
что уравнение прямо проходящей через точку А параллельно данной прямой можно записать: 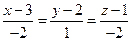 .
.
Ж)
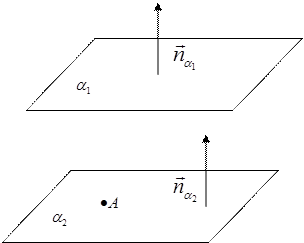 1.
1. 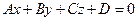 - канонический вид уравнения плоскости где A, B, C координаты вектора нормали
- канонический вид уравнения плоскости где A, B, C координаты вектора нормали 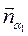 .
.
2. 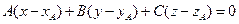 - уравнение искомой плоскости по заданной точке А и вектору нормали плоскости
- уравнение искомой плоскости по заданной точке А и вектору нормали плоскости 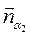 , где
, где 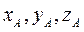 координаты точки А; A, B, C координаты вектора нормали
координаты точки А; A, B, C координаты вектора нормали 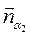 .
.
 3.
3. 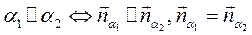 , т. к.
, т. к. 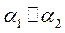 - по условию, то координаты вектора нормали
- по условию, то координаты вектора нормали 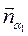 равны координатам вектора нормали
равны координатам вектора нормали 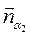 .
.
 4. Из
4. Из 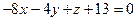 координаты вектора нормали
координаты вектора нормали 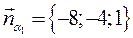 , но
, но 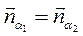
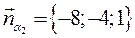
 5.
5. 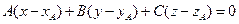
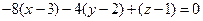
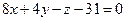
З)
1. 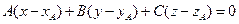 - уравнение искомой плоскости по заданной точке А и вектору нормали плоскости
- уравнение искомой плоскости по заданной точке А и вектору нормали плоскости 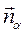 , где
, где 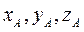 координаты точки А; A, B, C координаты вектора нормали
координаты точки А; A, B, C координаты вектора нормали 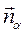 .
.
2. 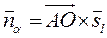
3. Прямая 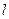 задана уравнением
задана уравнением 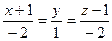 .
.  - канонический вид уравнения прямой, где
- канонический вид уравнения прямой, где 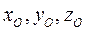 координаты точки О; m, n, p координаты направляющего вектора
координаты точки О; m, n, p координаты направляющего вектора 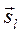
4. Тогда координаты точки 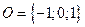 , а координаты направляющего вектора
, а координаты направляющего вектора 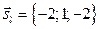 .
.
 5. Найдём координата вектора
5. Найдём координата вектора 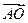 :
: 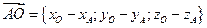
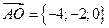
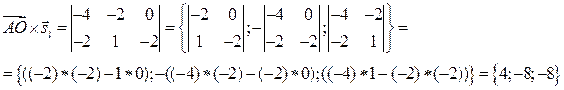 6.
6. 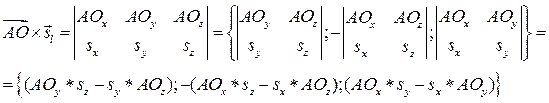
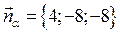 7. Тогда уравнение из пункта 1:
7. Тогда уравнение из пункта 1: 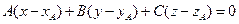 перепишем как:
перепишем как: 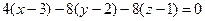
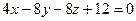
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|