1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 13 страница

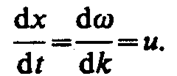(155. 1)

Скорость и есть групповая скорость. Ее можно определить как скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет. Выражение (155. 1) получено для волнового пакета из двух составляющих, однако можно доказать, что оно справедливо в самом общем случае.

Рассмотрим связь между групповой 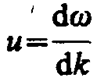(см. (155. 1)) и фазовой v=w /k (см. (154. 8)) скоростями. Учитывая, что k=2p/l (см. (154. 3)), получим

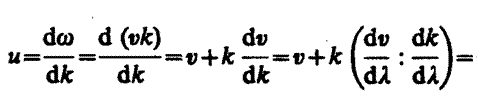
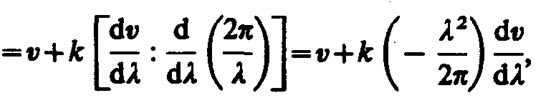
или

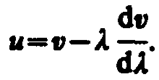(155. 2)

Из формулы (155. 2) вытекает, что u может быть как меньше, так и больше v в зависимости от знака dv/dl. В недиспергирующей среде dv/dl=0 и групповая скорость совпадает с фазовой.

Понятие групповой скорости очень важно, так как именно она фигурирует при измерении дальности в радиолокации, в системах управления космическими объектами и т. д. В теории относительности доказывается, что групповая скорость u< < с, в то время как для фазовой скорости ограничений не существует.

§ 156. Интерференция волн

Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности. Волны называются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. При наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих воли. Это явление называется интерференцией волн.

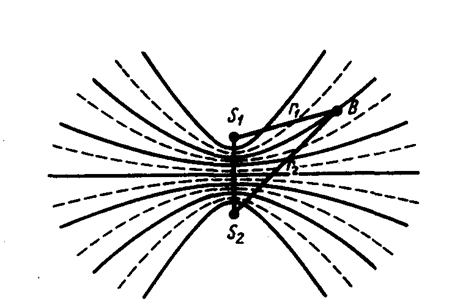
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S₁ и S₂ (рис. 221), колеблющимися с одинаковыми амплитудой А₀и частотой w и постоянной разностью фаз. Согласно (154. 7),

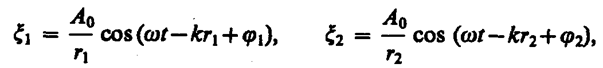
где r₁ и r₂ — расстояния от источников волн до рассматриваемой точки В, k — волновое число, j₁ и j₂ — начальные фазы обеих накладывающихся сферических волн. Амплитуда результирующей волны в точке В по (144. 2) равна

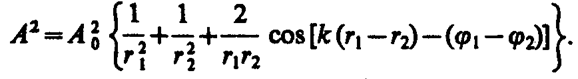
Так как для когерентных источников разность начальных фаз (j₁ – j₂) = const, то результат наложения двух волн в различных точках зависит от величины D = r₁ – r₂, называемой разностью хода волн.

В точках, где

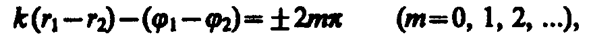(156. 1)

наблюдается интерференционный максимум: амплитуда результирующего колебания А=A₀/r₁ + A₀/r₂. В точках, где

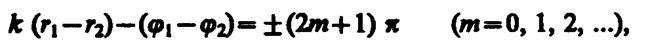(156. 2)

наблюдается интерференционный минимум: амплитуда результирующего колебания А=|A₀/r₁+A₀/r₂|; m=0, 1, 2, ..., называется соответственно порядком нтерференционного максимума или минимума.

Условия (156. 1) в (156. 2) сводятся к тому, что

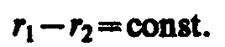(156. 3)

Выражение (156. 3) представляет собой уравнение гиперболы с фокусами в точках S₁ и S₂. Следовательно, геометрическое место точек, в которых наблюдается усиление или ослабление результирующего колебания, представляет собой семейство гипербол (рис. 221), отвечающих условию (j₁ – j₂)=0. Между двумя интерференционными максимумами (на рис. 221 сплошные линии) находятся интерференционные минимумы (на рис. 221 штриховые линии).

§ 157. Стоячие волны

Особым случаем интерференции являются стоячее волны — это волны, образующиеся при наложении двух бегущих воли, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией.

Для вывода уравнения стоячей волны предположим, что две плоские волны распространяются навстречу друг другу вдоль оси х в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат выберем в точке, в которой обе волны имеют одинаковую начальную фазу, а отсчет времени начнем с момента, когда начальные фазы обеих волн равны нулю. Тогда соответственно уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, будут иметь вид

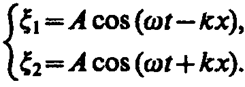(157. 1)

Сложив эти уравнения и учитывая, что k=2v/X (см. (154. 3)), получим уравнение стоячей волны:

(157. 2)

Из уравнения стоячей волны (157. 2) вытекает, что в каждой точке этой волны происходят колебания той же частоты w с амплитудой A_ст=|2А cos(2pх/l)|, зависящей от координаты х рассматриваемой точки.

В точках среды, где

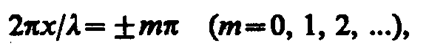(157. 3)

амплитуда колебаний достигает максимального значения, равного 2А. В точках среды, где

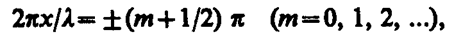(157. 4)

амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна (А_ст=2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (A_ст=0), называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают.

Из выражений (157. 3) и (157. 4) получим соответственно координаты пучностей и узлов:

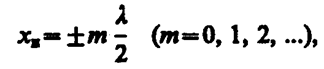(157. 5)

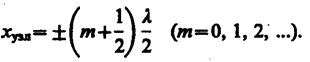(157. 6)

Из формул (157. 5) и (157. 6) следует, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны l/2. Расстояние между соседними пучностью и узлом стоячей волны равно l/4.

В отличие от бегущей волны, все точки которой совершают колебания с одинаковой амплитудой, но с запаздыванием по фазе (в уравнении (157. 1) бегущей волны фаза колебаний зависит от координаты х рассматриваемой точки), все точки стоячей волны между двумя узлами колеблются с разными амплитудами, но с одинаковыми фазами (в уравнении (157. 2) стоячей волны аргумент косинуса не зависит от х). При переходе через узел множитель 2Acos(2px/l) меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на p, т. е. точки, лежащие по разные стороны от узла, колеблются в противофазе.

Образование стоячих волн наблюдают при интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае возникает узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникает пучность (рис. 222, а), если более плотная — узел (рис. 222, б). Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний с противоположными фазами, в результате чего получается узел. Если же волна отражается от менее плотной среды, то изменения фазы не происходит и у границы колебания складываются с одинаковыми фазами — образуется пучность.

Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, так как падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узловыми точками, остается постоянной. Лишь в пределах расстояний, равных половине длины волны, происходят взаимные превращения кинетической энергии в потенциальную и обратно.

Глава 20Электромагнитные волны

§ 161. Экспериментальное получение электромагнитных волн

Существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью, — вытекает из уравнений Максвелла (см. § 139). Уравнения Максвелла сформулированы в 1865 г. на основе обобщения эмпирических законов электрических и магнитных явлений. Как уже указывалось, решающую роль для утверждения максвелловской теории сыграли опыты Герца (1888), доказавшие, что электрические и магнитные поля действительно распространяются в виде воли, поведение которых полностью описывается уравнениями Максвелла.

Источником электромагнитных волн в действительности может быть любой электрический колебательный контур ила проводник, по которому течет переменный электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором переменное электромагнитное поле создается. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры, так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное — внутри катушки индуктивности.

Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их (рис. 225, а, б), совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представляющему собой два стрежня, разделенных искровым промежутком (рис. 225, в). Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора (рис. 225, а), то в открытом оно заполняет окружающее контур пространство (рис. 255, в), что существенно повышает интенсивность электромагнитного излучения. Колебания в такой системе поддерживаются за счет источника э. д. с., подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

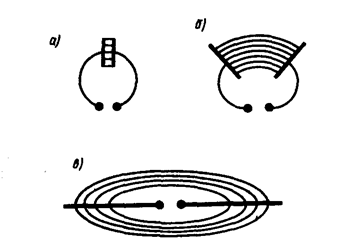
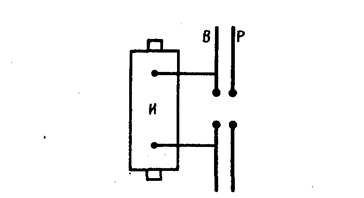
Для возбуждения электромагнитных воли вибратор Герца В подключался к индуктору И (рис. 226). Когда напряжение на искровом промежутке достигало пробивного значения, возникала искра, закорачивающая обе половины вибратора, и в нем возникали свободные затухающие колебания. При исчезновении искры контур размыкался и колебания прекращались. Затем индуктор снова заряжал конденсатор, возникала искра и в контуре опять наблюдались колебания и т. д. Для регистрации электромагнитных воли Герц пользовался вторым вибратором, называемым резонатором Р, имеющим такую же частоту собственных колебаний, что и излучающий вибратор, т. е. настроенным в резонанс с вибратором. Когда электромагнитные волны достигали резонатора, то в его зазоре проскакивала электрическая искра.

С помощью описанного вибратора Герц экспериментировал с электромагнитными волнами, длина волны которых составляла примерно 3 м. П. Н. Лебедев, применяя миниатюрный вибратор из тонких платиновых стерженьков, получил миллиметровые электромагнитные волны с l = 6 – 4 мм. Дальнейшее развитие методики эксперимента в этом направлении позволило в 1923 г. российскому физику А. А. Глаголевой-Аркадьевой (1884—1945) сконструировать массовый излучатель, в котором короткие электромагнитные волны, возбуждаемые колебаниями электрических зарядов в атомах и молекулах, генерировались с помощью искр, проскакиваемых между металлическими опилками, взвешенными в масле. Так были получены волны с l от 50 мм до 80 мкм. Тем самым было доказано существование волн, перекрывающих интервал между радиоволнами и инфракрасным излучением.

Недостатком вибраторов Герца и Лебедева и массового излучателя Глаголевой-Аркадьевой являлось то, что свободные колебания в них быстро затухали и обладали малой мощностью. Для получения незатухающих колебаний необходимо создать автоколебательную систему (см. § 146), которая обеспечивала бы подачу энергии с частотой, равной частоте собственных колебаний контура. Поэтому в 20-х годах нашего столетия перешли к генерированию электромагнитных волн с помощью электронных ламп. Ламповые генераторы позволяют получать колебания заданной (практически любой) мощности и синусоидальной формы.

Электромагнитные волны, обладая широким диапазоном частот (или длин волн l=c/n, где с — скорость электромагнитных волн в вакууме), отличаются друг от друга по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны делятся на несколько видов: радиоволны, световые волны, рентгеновское и g-излучения (табл. 5). Следует отметить, что границы между различными видами электромагнитных волн довольно условны.

Таблица 5

Продолжение табл. 5

§ 162. Дифференциальное уравнение электромагнитной волны

Как уже указывалось (см. § 161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных воли. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154. 9):

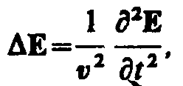(162. 1)

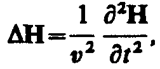(162. 2)

где 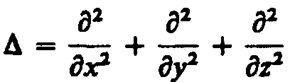— оператор Лапласа, v — фазовая скорость.

Всякая функция, удовлетворяющая уравнениям (162. 1) и (162. 2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных воли определяется выражением

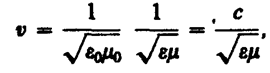(162. 3)

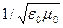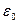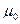где с = , и — соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.

В вакууме (при e=1 и m=l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em > 1, то скорость распространения электромагнитных воли в веществе всегда меньше, чем в вакууме.

При вычислении скорости распространения электромагнитного поля по формуле (162. 3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость e и m от частоты. Совпадение же размерного коэффициента в (162. 3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.

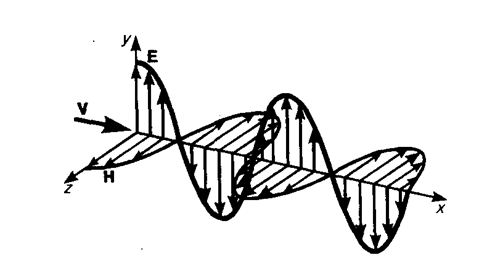
Следствием теории Максвелла является поперечность электромагнитных волн: векторы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 227 показана моментальная «фотография» плоской электромагнитной волны) и лежат в плоскости, перпендикулярной вектору v скорости распространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н всегда колеблются в одинаковых фазах (см. рис. 227), причем мгновенные значения Е и Н в любой точке связаны соотношением

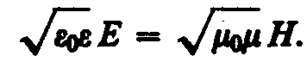(162. 4)

Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и т. д. От уравнений (162. 1) и (162. 2) можно перейти к уравнениям

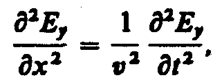(162. 5)

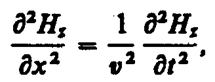(162. 6)

где соответственно индексы у и z при Е и Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей y и z.

Уравнениям (162. 5) и (162. 6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями

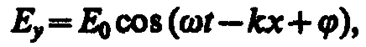(162. 7)

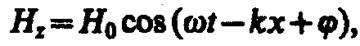(162. 8)

где E₀ и Н₀ — соответственно амплитуды напряженностей электрического и магнитного полей волны, w — круговая частота волны, k=w/v — волновое число, j — начальные фазы колебаний в точках с координатой х=0. В уравнениях (162. 7) и (162. 8) j одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят в одинаковых фазах.

§ 163. Энергия электромагнитных волн. Импульс электромагнитного поля

Возможность обнаружения электромагнитных воли указывает на то, что они переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей w_эл (см. (95. 8)) и w_м, (см. (130. 3)) электрического и магнитного полей:

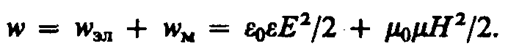
Учитывая выражение (162. 4), получим, что плотности энергии электрического и магнитного полей в каждый момент времени одинаковы, т. е. w_эл = w_м. Поэтому

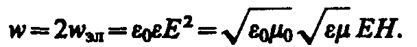
Умножив плотность энергии w на скорость v распространения волны в среде (см. (162. 3)), получим модуль плотности потока энергии:

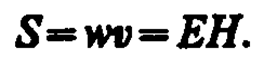
Tax как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ЕН] совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова — Пойнтинга:

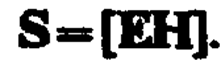
Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно мало. Можно оценить, что при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших классическими, П. Н. Лебедев в 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. — на газы. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны.

Существование давления электромагнитных воли приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля

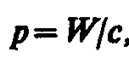
где W — энергия электромагнитного поля. Выражая импульс как р=тс (поле в вакууме распространяется со скоростью с), получим р=тс= W/c, откуда

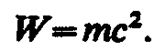(163. 1)

Это соотношение между массой и энергией электромагнитного поля является универсальным законом природы (см. также § 40). Согласно специальной теории относительности, выражение (163. 1) имеет общее значение и справедливо для любых тел независимо от их внутреннего строения.

Таким образом, рассмотренные свойства электромагнитных волн, определяемые теорией Максвелла, полностью подтверждаются опытами Герца, Лебедева и выводами специальной теории относительности, сыгравшими решающую роль для подтверждения и быстрого признания этой теории.

§ 164. Излучение диполя. Применение электромагнитных волн

Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону

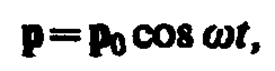
где р₀ — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда +Q и отрицательного заряда –Q, гармонически колеблющегося вдоль направления р с частотой w.

Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчитывать рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колебания около их положений равновесия.

Характер электромагнитного поля диполя зависит от выбора рассматриваемой точки. Особый интерес представляет так называемая волновая зона диполя — точки пространства, отстоящие от диполя на расстояниях r, значительно превышающих длину волны (r> > l), — так как в ней картина электромагнитного поля диполя сильно упрощается. Это связано с тем, что в волновой зоне диполя практически остаются только «отпочковавшиеся» от диполя, свободно распространяющиеся поля, в то время как поля, колеблющиеся вместе с диполем и имеющие более сложную структуру, сосредоточены в области расстояний r < l.

Если волна распространяется в однородной изотропной среде, то время прохождения волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излучаемая диполем, есть сферическая волна.

В каждой точке векторы Е и Н колеблются по закону cos(wt—kr), амплитуды этих векторов пропорциональны (1/r) sinq (для вакуума), т. е. зависят от расстояния r до излучателя и угла q между направлением радиуса-вектора и осью диполя. Отсюда следует, что интенсивность излучения диполя в волновой зоне

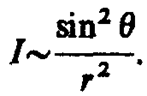(164. 1)

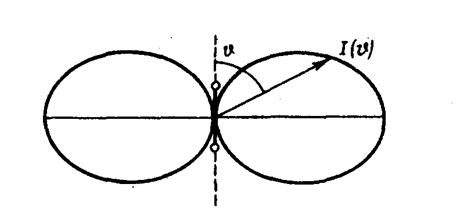
Зависимость (164. 1) I от q при заданном значении r, приводимая в полярных координатах (рис. 228), называется диаграммой направленности излучения диполя. Как видно из выражения (164. 1) и приведенной диаграммы, диполь сильнее всего излучает в направлениях, перпендикулярных его оси (q = p/2). Вдоль своей оси (q =0 и q =p) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн.

Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А. С. Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль для распространения и развития теории Максвелла.

Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолокации — обнаружения предметов (например, самолетов, кораблей и т. д. ) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолокации используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д.

Для электромагнитных волн характерно явление дифракции — огибания волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устойчивая радиосвязь между удаленными пунктами, разделенными между собой выпуклостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототелеграфии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радиогеодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки и техники, где бы они не использовались.

ОГЛАВЛЕНИЕ

ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ..... 116

Глава 11Электростатика........................................................................................ 116

§ 77. Закон сохранения электрического заряда............................................... 116

§ 78. Закон Кулона................................................................................................ 117

§ 79. Электростатическое поле. Напряженность электростатического поля 117

§ 80. Принцип суперпозиции электростатических полей. Поле диполя..... 119

§ 81. Теорема Гаусса для электростатического поля в вакууме................... 120

§ 82. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме..................................................................................................... 122

§ 83. Циркуляция вектора напряженности электростатического поля....... 124

§ 84. Потенциал электростатического поля..................................................... 125

§ 85. Напряженность как градиент потенциала. Эквипотенциальные поверхности............................................................................................................ 126

§ 86. Вычисление разности потенциалов по напряженности поля............... 127

⇐ Предыдущая 5 6 7 8 9 10 11 121314 Следующая ⇒

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результиру­ющего колебания А равна сумме амплитуд складываемых колебаний; 13 страница

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 13 страница