1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 11 страница

Любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте w₀:

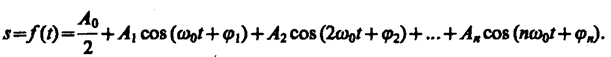(144. 5)

Представление периодической функции в виде (144. 5) связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье. * Слагаемые ряда Фурье, определяющие гармонические колебания с частотами w₀, 2w₀, 3w₀, ..., называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания.

* Ж. Фурье (1768—1830) — французский ученый.

§ 145. Сложение взаимно перпендикулярных колебаний

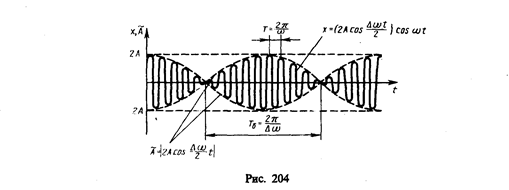
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты w, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем

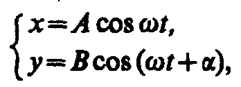(145. 1)

где a — разность фаз обоих колебаний, А и В — амплитуды складываемых колебаний. Уравнение траектории результирующего колебания находится исключением из выражений (145. 1) параметра t. Записывая складываемые колебания в виде

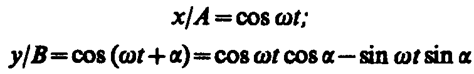
и заменяя во втором уравнении coswt на х/А и sinwt на 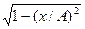, получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно:

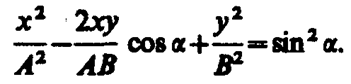(145. 2)

Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз a. Рассмотрим некоторые частные случаи, представляющие физический интерес:

1) a = mp(m=0, ±1, ±2, ... ). В данном случае эллипс вырождается в отрезок прямой

(145. 3)

где знак плюс соответствует нулю и четным значениям т (рис. 205, а), а знак минус — нечетным значениям т (рис. 205, б). Результирующее колебание является гармоническим колебанием с частотой w и амплитудой 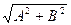, совершающимся вдоль прямой (145. 3), составляющей с осью х угол j=arctg 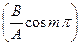. В данном случае имеем дело с линейно поляризованными колебаниями;

2) a = (2m+1) 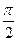(m=0, ± 1, ±2,... ). В данном случае уравнение примет вид

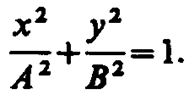(145. 4)

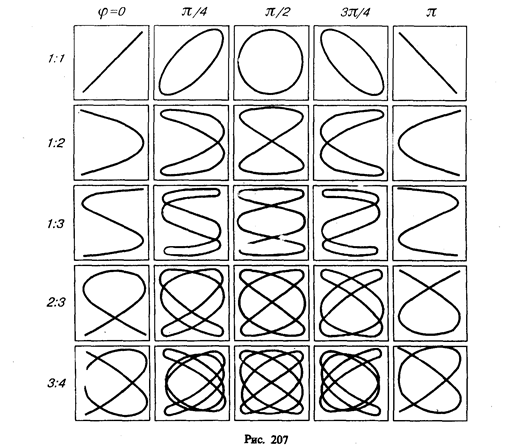
Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 206). Кроме того, если А=В, то эллипс (145. 4) вырождается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.

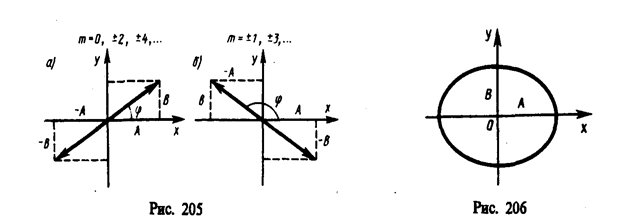
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. * Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 207 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху; разность фаз принимается равной j).

* Ж. Лиссажу (1822—1880) — французский физик.

Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Поэтому анализ фигур Лиссажу — широко используемый метод исследования соотношений частот и разности фаз складываемых колебаний, а также формы колебаний.

§ 146. Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания

Рассмотрим свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

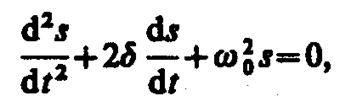(146. 1)

где s – колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания, w₀ — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Решение уравнения (146. 1) рассмотрим в виде

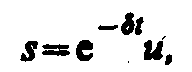(146. 2)

где u=u(t). После нахождения первой и второй производных выражения (146. 2) и подстановки их в (146. 1) получим

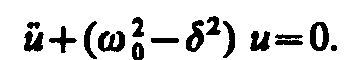(146. 3)

Решение уравнения (146. 3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:

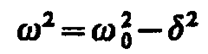(146. 4)

(если ( 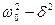)> 0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа (142. 1) ü +w²и=0, решением которого является функция и=А₀cos(wt+j)(см. (140. 1)). Таким образом, решение уравнения (146. 1) в случае малых затуханий ( )

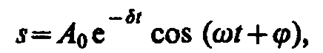(146. 5)

где

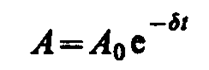(146. 6)

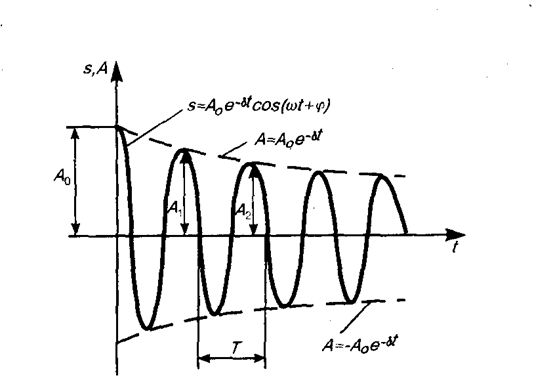
— амплитуда затухающих колебаний, а А₀ — начальная амплитуда. Зависимость (146. 5) показана на рис. 208 сплошной линией, а зависимость (146. 6) — штриховыми линиями. Промежуток времени t=1/d, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 208). Тогда период затухающих колебаний с учетом формулы (146. 4) равен

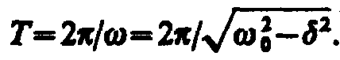
Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

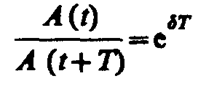
называется декрементом затухания, а его логарифм

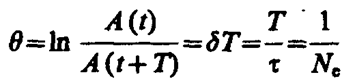(146. 7)

— логарифмическим декрементом затухания; N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна

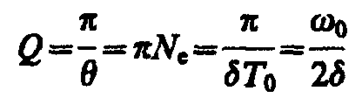(146. 8)

(так как затухание мало ( 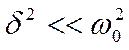), то T принято равным Т₀).

Из формулы (146. 8) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

Выводы, полученные для свободных затухающих колебаний линейных систем, применимы для колебаний различной физической природы — механических (в качестве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический колебательный контур).

1. Свободные затухающие колебания пружинного маятника. Для пружинного маятника (см. § 142) массой т, совершающего малые колебания под действием упругой силы F= —kx, сила трения пропорциональна скорости, т. е.

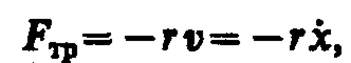
где r — коэффициент сопротивления; знак минус указывает на противоположные направления силы трения и скорости

При данных условиях закон движения маятника будет иметь вид

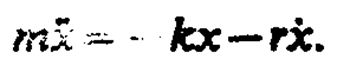(146. 9)

Используя формулу w₀= 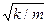(см. (142. 2)) и принимая, что коэффициент затухания

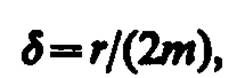(146. 10)

получим идентичное уравнению (146. 1) дифференциальное уравнение затухающих колебаний маятника:

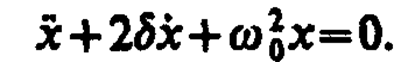
Из выражений (146. 1) и (146. 5) вытекает, что колебания маятника подчиняются закону

где частота 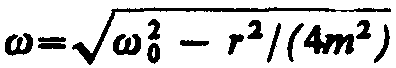(см. (146. 4)).

Добротность пружинного маятника, согласно (146. 8) и (146. 10), Q= 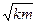/r.

2. Свободные затухающие колебания в электрическом колебательном контуре. Дифференциальное уравнение свободных затухающих колебаний заряда в контуре (при R¹ 0) имеет вид (см. (143. 2))

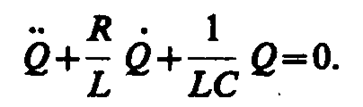
Учитывая выражение (143. 4) и принимая коэффициент затухания

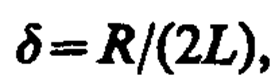(146. 11)

дифференциальное уравнение (143. 2) можно записать в идентичном уравнению (146. 1) виде

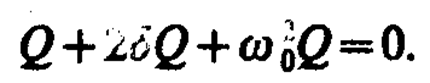
Из выражений (146. 1) и (146. 5) вытекает, что колебания заряда совершаются по закону

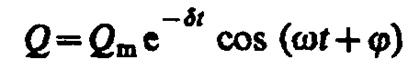(146. 12)

с частотой, согласно (146. 4),

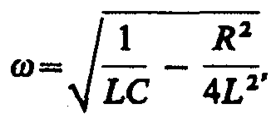(146. 13)

меньшей собственной частоты контура w₀ (см. (143. 4)). При R=0 формула (146. 13) переходит в (143. 4).

Логарифмический декремент затухания определяется формулой (146. 7), а добротность колебательного контура (см. (146. 8))

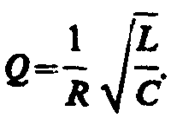(146. 14)

В заключение отметим, что при увеличении коэффициента затухания d период затухающих колебании растет и при d=w₀ обращается в бесконечность, т. е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t®¥. Процесс не будет колебательным. Он называется апериодическим.

Огромный интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Особенно важны и широко применимы так называемые автоколебания — незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.

Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний (см. § 147), происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).

Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй.

Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т. д.

§ 147. Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону:

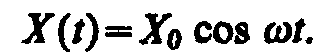
Если рассматривать механические колебания, то роль X(t) играет внешняя вынуждающая сила

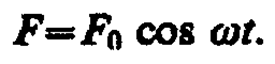(147. 1)

С учетом (147. 1) закон движения для пружинного маятника (146. 9) запишется в виде

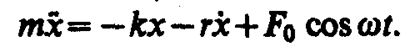
Используя (142. 2) и (146. 10), придем к уравнению

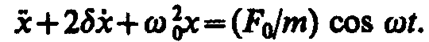(147. 2)

Если рассматривать электрический колебательный контур, то роль X(t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э. д. с. или переменное напряжение

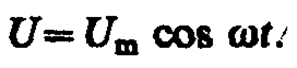(147. 3)

Тогда уравнение (143. 2) с учетом (147. 3) можно записать в виде

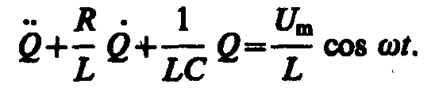
Используя (143. 4) и (146. 11), придем к уравнению

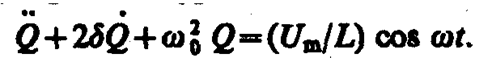(147. 4)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э. д. с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

Уравнения (147. 2) и (147. 4) можно свести к линейному неоднородному дифференциальному уравнению

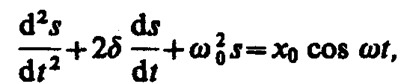(147. 5)

применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x₀ в случае механических колебаний равно F₀/m, в случае электромагнитных — U_m/L).

Решение уравнения (147. 5) равно сумме общего решения (146. 5) однородного уравнения (146. 1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме (см. § 140). Заменим правую часть уравнения (147. 5) на комплексную величину х₀ :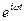

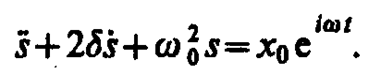(147. 6)

Частное решение этого уравнения будем искать в виде

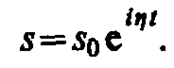
Подставляя выражение для s и его производных 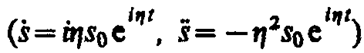в уравнение (147. 6), получаем

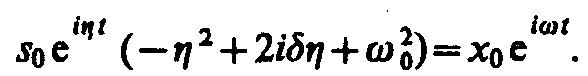(147. 7)

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h=w. Учитывая это, из уравнения (147. 7) найдем величину s₀ и умножим ее числитель и знаменатель на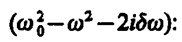

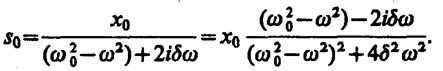
Это комплексное число удобно представить в экспоненциальной форме:

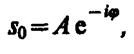
где

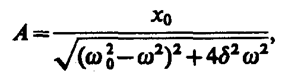(147. 8)

(147. 9)

Следовательно, решение уравнения (147. 6) в комплексной форме примет вид

Его вещественная часть, являющаяся решением уравнения (147. 5), равна

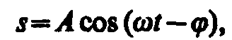(147. 10)

где А и j задаются соответственно формулами (147. 8) и (147. 9).

Таким образом, частное решение неоднородного уравнения (147. 5) имеет вид

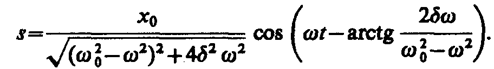(147. 11)

Решение уравнения (147. 5) равно сумме общего решения однородного уравнения

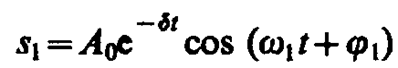(147. 12)

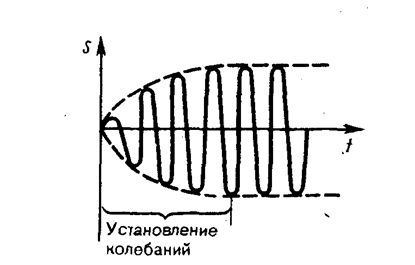
(см. (146. 5)) и частного решения (147. 11). Слагаемое (147. 12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147. 8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147. 8) и (147. 9), также зависят от w.

Запишем формулы (147. 10), (147. 8) и (147. 9) для электромагнитных колебаний, учитывая, что 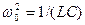(см. (143. 4)) и 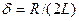(см. (146. 11)):

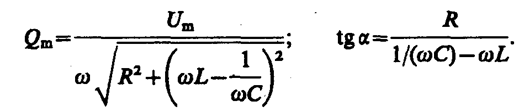(147. 13)

Продифференцировав Q=Q_mcos(wt–a) по t, найдем силу тока в контуре при установившихся колебаниях:

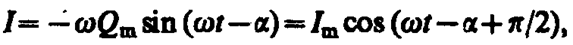(147. 14)

где

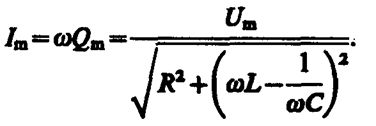(147. 15)

Выражение (147. 14) может быть записано в ввде

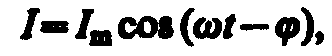
где j=a – p/2 — сдвиг по фазе между током и приложенным напряжением (см. (147. 3)). В соответствии с выражением (147. 13)

(147. 16)

Из формулы (147. 16) вытекает, что ток отстает по фазе от напряжения (j> 0), если wL> 1/(wС), и опережает напряжение (j< 0), если wL< 1/(wС).

Формулы (147. 15) и (147. 16) можно также получить с помощью векторной диаграммы. Это сделано в §149 для переменных токов.

§ 148. Амплитуда и фаза вынужденных колебаний (механических и электромагнитных). Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты w. Механические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.

Из формулы (147. 8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту w_рез, — частоту, при которой амплитуда А смещения (заряда) достигает максимума, — нужно найти максимум функции (147. 8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по w и приравняв его нулю, получим условие, определяющее w_рез:

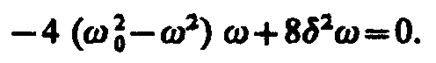
Это равенство выполняется при w=0, ± 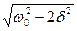, у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота

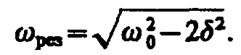(148. 1)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При значение w_рез практически совпадает с собственной частотой w₀ колебательной системы. Подставляя (148. 1) в формулу (147. 8), получим

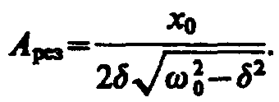(148. 2)

На рис. 210 приведены зависимости амплитуды вынужденных колебаний от частоты при различных значениях d. Из (148. 1) и (148. 2) вытекает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w® 0, то все кривые (см. также (147. 8)) достигают одного в того же, отличного от нуля, предельного значения 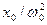, которое называют статическим отклонением. В случае механических колебаний , в случае электромагнитных – U_m/(L 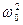). Если w®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

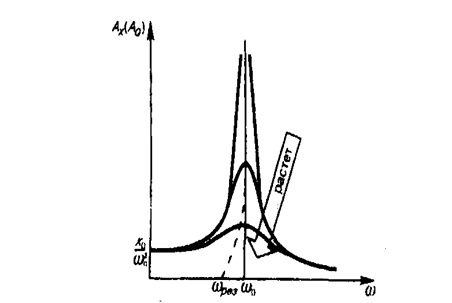
Из формулы (148. 2) вытекает, что при малом затухании ( ) резонансная амплитуда смещения (заряда)

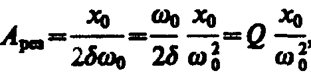
где Q — добротность колебательной системы (см. (146. 8)), 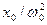— рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А_рез.

На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока)

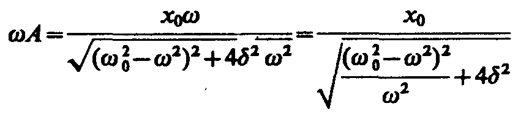
максимальна при w_рез=w₀ и равна , т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. Используя формулы (142. 2), (146. 10) и (143. 4), (146. 11), получим, что амплитуда скорости при механическом резонансе равна

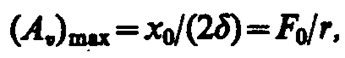
а амплитуда тока при электрическом резонансе

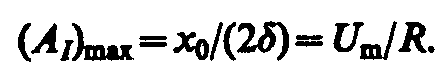
Из выражения tgj = 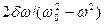(см. (147. 9)) следует, что если затухание в системе отсутствует (d=0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹ 0.

Зависимость j от w при разных коэффициентах d графически представлена на рис. 212, из которого следует, что при изменении w изменяется и сдвиг фаз j. Из формулы (147. 9) вытекает, что при w=0 j=0, а при w=w₀ независимо от значения коэффициента затухания j = p/2, т. е. сила (напряжение) опережает по фазе колебания на p/2. При дальнейшем увеличении w сдвиг фаз возрастает и при w> > w₀ j ® p, т. е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.

§ 148. Переменный ток

Установившиеся вынужденные электромагнитные колебания (см. § 147) можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа, которые будут использованы применительно к переменным токам (эти законы уже использовались при рассмотрении электромагнитных колебаний).

Рассмотрим последовательно процессы, происходящие на участке цепи, содержащем резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение

⇐ Предыдущая 5 6 7 8 9 101112 13 14 Следующая ⇒

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результиру­ющего колебания А равна сумме амплитуд складываемых колебаний; 11 страница

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 11 страница