1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 10 страница

Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3× 10⁸ м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.

К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.

Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.

Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Taк, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.

Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.

4 КОЛЕБАНИЯ И ВОЛНЫ

Глава 18 Механические и электромагнитные колебания

§ 140. Гармонические колебания и их характеристики

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Например, единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д. У. Рэлеем (1842—1919), А. Г. Столетовым, русским инженером-экспериментатором П. Н. Лебедевым (1866—1912). Большой вклад в развитие теории колебаний внесли Л. И. Мандельштам (1879—1944) и его ученики.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

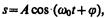(140. 1)

где А — максимальное значение колеблющейся величины, называемое амплитудой колебания, w₀ — круговая (циклическая) частота, j — начальная фаза колебания в момент времени t=0, (w₀t+j) — фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то s может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2p, т. е.

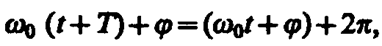
откуда

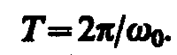(140. 2)

Величина, обратная периоду колебаний,

(140. 3)

т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140. 2) и (140. 3), получим

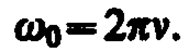
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

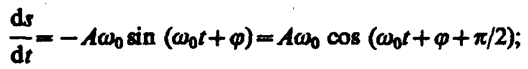(140. 4)

(140. 5)

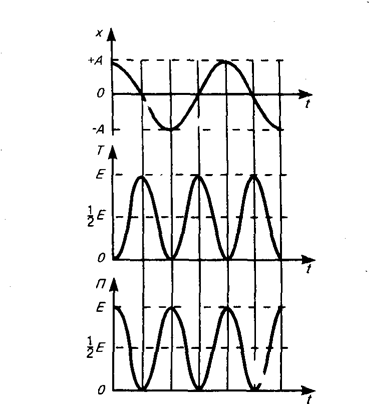
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140. 4) и (140. 5) соответственно равны Аw₀ и Аw 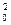. Фаза величины (140. 4) отличается от фазы величины (140. 1) на p/2, а фаза величины (140. 5) отличается от фазы величины (140. 1) на p. Следовательно, в моменты времени, когда s=0, ds/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d²s/dt² приобретает наибольшее положительное значение (рис. 198).

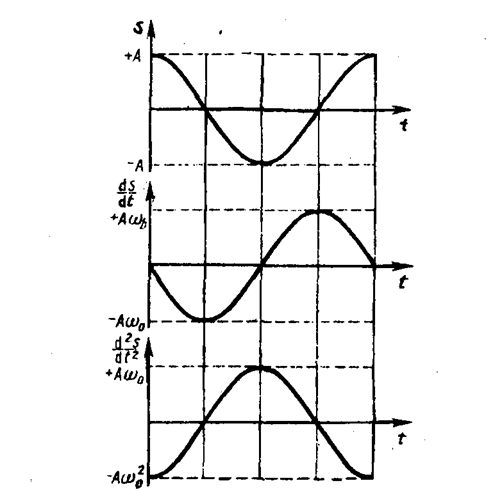
Из выражения (140. 5) следует дифференциальное уравнение гармонических колебаний

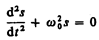(140. 6)

(где s = A cos (w₀t+j)). Решением этого уравнения является выражение (140. 1).

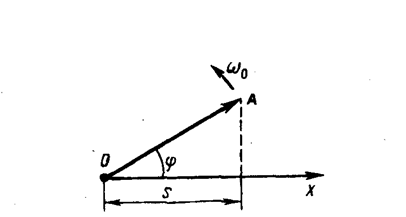
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси х, под углом j, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис. 199). Если этот вектор привести во вращение с угловой скоростью w₀, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s=A cos (w₀t+j). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом j, равным начальной фазе, и вращающегося с угловой скоростью w₀ вокруг этой точки.

В физике часто применяется другой метод, который отличается от метода вращающегося вектора амплитуды лишь по форме. В этом методе колеблющуюся величину представляют комплексным числом. Согласно формуле Эйлера, для комплексных чисел

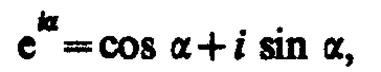(140. 7)

где 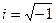— мнимая единица. Поэтому уравнение гармонического колебания (140. 1) можно записать в комплексной форме:

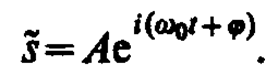(140. 8)

Вещественная часть выражения (140. 8)

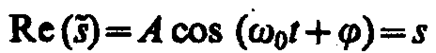
представляет собой гармоническое колебание. Обозначение Re вещественной части условимся опускать и (140. 8) будем записывать в виде

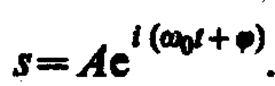
В теории колебаний принимается, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.

§ 141. Механические гармонические колебания

Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением, аналогичным уравнению (140. 1), где s=x:

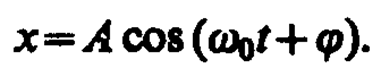(141. 1)

Согласно выражениям (140. 4) в (140. 5), скорость v и ускорение а колеблющейся точки соответственно равны

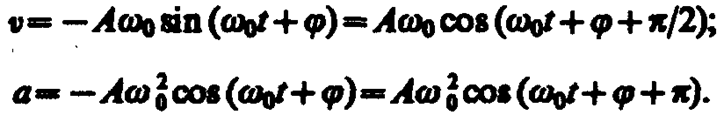(141. 2)

Сила F=ma, действующая на колеблющуюся материальную точку массой т, с учетом (141. 1) и (1412) равна

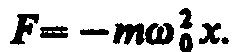
Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна

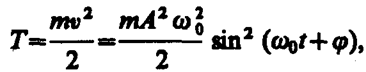(141. 3)

или

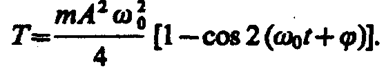(141. 4)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна

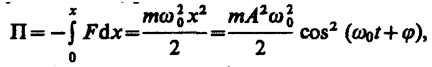(141. 5)

или

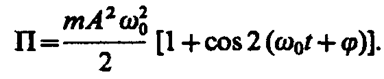(141. 6)

Сложив (141. 3) и (141. 5), получим формулу для полной энергии:

(141. 7)

Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.

Из формул (141. 4) и (141. 6) следует, что Т и П изменяются с частотой 2w₀, т. е. с частотой, которая в два раза превышает частоту гармонического колебания. На рис. 200 представлены графики зависимости x, T и П от времени. Так как á sin²añ = á cos²añ = 1/2, то из формул (141. 3), (141. 5) и (14l. 7) следует, что á Tñ = á Пñ = ½ E.

§ 142. Гармонический осциллятор. Пружинный, физический и математический маятники

Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида (140. 6);

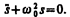(142. 1)

Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур (для токов и напряжений столь малых, что элементы контура можно было бы считать линейными; см. §146).

1. Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника

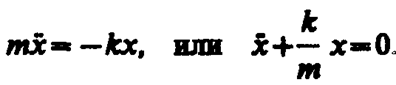
Из выражений (142. 1) и (140. 1) следует, что пружинный маятник совершает гармонические колебания по закону х=А соs (w₀t + j) с циклической частотой

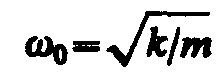(142. 2)

и периодом

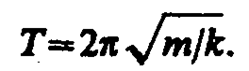(142. 3)

Формула (142. 3) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (см. (21. 3)), т. е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (141. 5) и (142. 2), равна

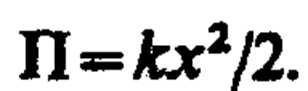
2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 201).

Если маятник отклонен из положения равновесия на некоторый угол a, то в соответствии с уравнением динамики вращательного движения твердого тела (18. 3) момент M возвращающей силы можно записать в виде

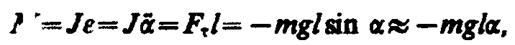(142. 4)

где J — момент инерции маятника относительно оси, проходящей через точку подвеса О, l – расстояние между ней и центром масс маятника, F_t= –mg sina » –mga. — возвращающая сила (знак минус обусловлен тем, что направления F_t и a всегда противоположны; sina »a соответствует малым колебаниям маятника, т. е. малым отклонениям маятника из положения равновесия). Уравнение (142. 4) можно записать в виде

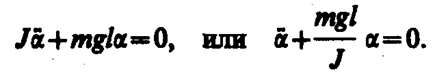
Принимая

(142. 5)

получим уравнение

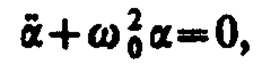
идентичное с (142. 1), решение которого (140. 1) известно:

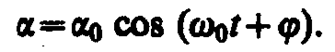(142. 6)

Из выражения (142. 6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w₀ (см. (142. 5)) и периодом

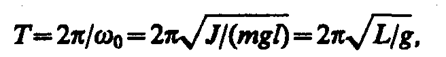(142. 7)

где L=J/(ml) — приведенная длина физического маятника.

Точка О' на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 201). Применяя теорему Штейнера (16. 1), получим

т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса

станет новым центром качаний, и период колебаний физического маятника не изменится.

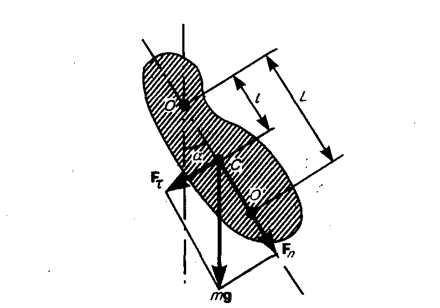
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника

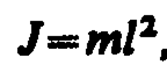(142. 8)

где l — длина маятника.

Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив выражение (142. 8) в формулу (1417), получим выражение для периода малых колебаний математического маятника

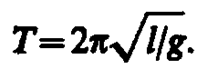(142. 9)

Сравнивая формулы (142. 7) и (142. 9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

§ 143. Свободные гармонические колебания в колебательном контуре

Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.

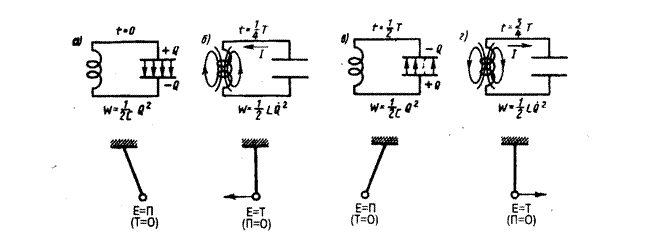
Рассмотрим последовательные стадии колебательного процесса в идеализированном контуре, сопротивление которого пренебрежимо мало (R»0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Тогда в начальный момент времени t=0 (рис. 202, а) между обкладками конденсатора возникнет электрическое поле, энергия которого 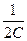Q² (см. (95. 4)). Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (она равна — возрастать.

Так как R»0, то, согласно закону сохранения энергии, полная энергия

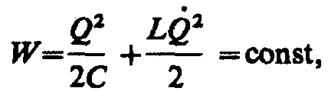
так как она на нагревание не расходуется. Поэтому в момент t=¼ T, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения (рис. 202, б). Начиная с этого момента ток в контуре будет убывать; следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцируется ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который в конце концов обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 202, в). Далее те же процессы начнут протекать в обратном направлении (рис. 202, г) и система к моменту времени t=Т придет в первоначальное состояние (рис. 202, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т. е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей.

Электрические колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рис. 202 внизу), сопровождающимися взаимными превращениями потенциальной и кинетической энергий маятника. В данном случае энергия электрического поля конденсатора (Q²/(2C)) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ²/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L играет роль массы т, а сопротивление контура — роль силы трения, действующей на маятник.

Согласно закону Ома, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R,

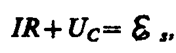
где IR—напряжение на резисторе, Uc=Q/C—напряжение на конденсаторе, 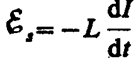– э. д. с. самоиндукции, возникающая в катушке при протекании в ней переменного тока ( 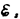– единственная э. д. с. в контуре). Следовательно,

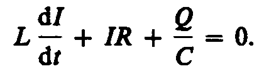(143. 1)

Разделив (143. 1) на L и подставив 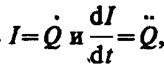получим дифференциальное уравнение колебаний заряда Q в контуре:

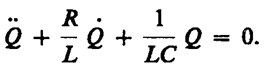(143. 2)

В данном колебательном контуре внешние э. д. с. отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания (см. §140). Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из (143. 2) получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре.

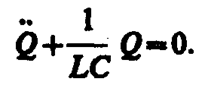
Из выражений (142. 1) и (140. 1) вытекает, что заряд Q совершает гармонические колебания по закону

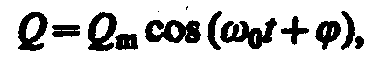(143. 3)

где Q_m — амплитуда колебаний заряда конденсатора с циклической частотой w₀, называемой собственной частотой контура, т. е.

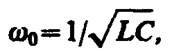(143. 4)

и периодом

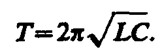(143. 5)

Формула (143. 5) впервые была получена У. Томсоном и называется формулой Томсона. Сила тока в колебательном контуре (см. (140. 4))

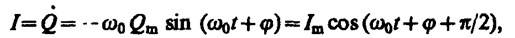(143. 6)

где I_m=w₀Q_m — амплитуда силы тока. Напряжение на конденсаторе

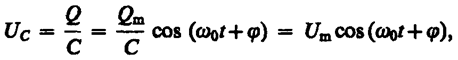(143. 7)

где U_m=Q_m/C—амплитуда напряжения.

Из выражений (143. 3) и (143. 6) вытекает, что колебания тока I опережают по фазе колебания заряда Q на p/2, т. е., когда ток достигает максимального значения, заряд (а также и напряжение (см. (143. 7)) обращается в нуль, и наоборот.

§ 144. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты

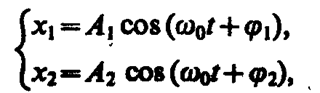
воспользовавшись методом вращающегося вектора амплитуды (см. § 140). Построим векторные диаграммы этих колебаний (рис. 203).

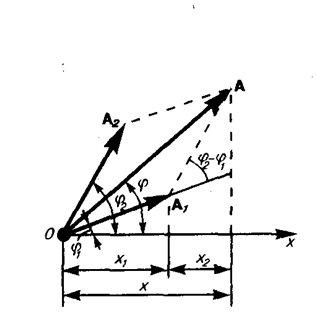
Taк как векторы A₁ и А₂ вращаются с одинаковой угловой скоростью w₀, то разность фаз (j₂—j₁)между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет

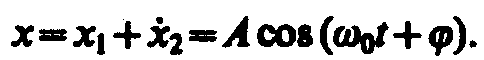(144. 1)

В выражении (144. 1) амплитуда А и начальная фаза j соответственно задаются соотношениями

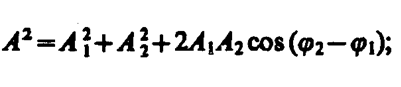(144. 2)

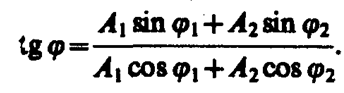
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (j₂—j₁) складываемых колебаний.

Проанализируем выражение (144. 2) в зависимости от разности фаз (j₂—j₁):

1) j2—j1 = ±2mp (т=0, 1, 2, ... ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) j₂—j₁= ±(2m+1)p (т=0, 1, 2, ... ), тогда A=|A₁–A₂|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.

Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.

Пусть амплитуды складываемых колебаний равны А, а частоты равны w и w+Dw, причем Dw< < w. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

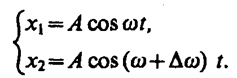
Складывая эти выражения и учитывая, что во втором сомножителе Dw/2< < w, найдем

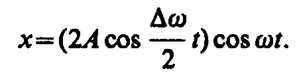(144. 3)

Результирующее колебание (144. 3) можно рассматривать как гармоническое с частотой w, амплитуда А_б, которого изменяется по следующему периодическому закону:

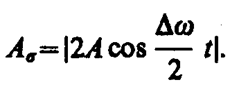(144. 4)

Частота изменения А_б в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:

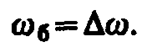
Период биений

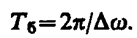
Характер зависимости (144. 3) показан на рис. 204, где сплошные жирные линии дают график результирующего колебания (144. 3), а огибающие их — график медленно меняющейся по уравнению (144. 4) амплитуды.

Определение частоты тона (звука определенной высоты (см. § 158)) биений между эталонным и измеряемым колебаниями — наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результиру­ющего колебания А равна сумме амплитуд складываемых колебаний; 10 страница

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 10 страница