1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 6 страница

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165).

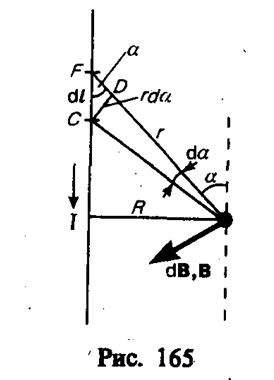
В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что

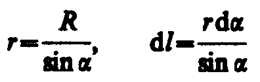
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110. 2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

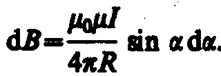(110. 4)

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110. 3) и (110. 4),

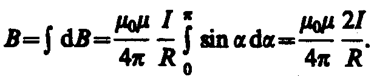
Следовательно, магнитная индукция поля прямого тока

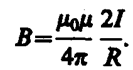(110. 5)

2. Магнитное поле в центре кругового проводника с током (рис. 166).

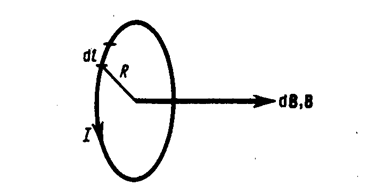
Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110. 2),

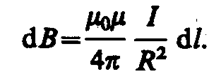
Тогда

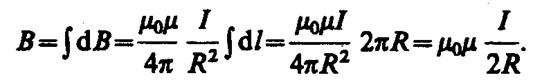
Следовательно, магнитная индукция поля в центре кругового проводника с током

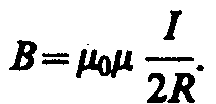
§ 111. Закон Ампера. Взаимодействие параллельных токов

Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током. Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, равна

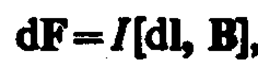(111. 1)

где dl—вектор, по модулю равный dl и совпадающий по направлению с током, В — вектор магнитной индукции.

Направление вектора dF может быть найдено, согласно (111. 1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111. 1)) вычисляется по формуле

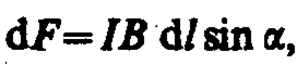(111. 2)

где a — угол между векторами dl и В.

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂; (направления токов указаны на рис. 167),

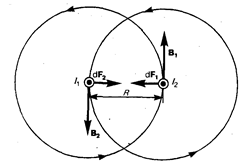
расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током I₂. Ток I₁ создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B₁ определяется правилом правого винта, его модуль по формуле (110. 5) равен

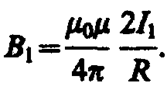
Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111. 2), с учетом того, что угол a между элементами тока I₂ и вектором B₁ прямой, равен

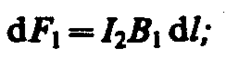
подставляя значение для В₁, получим

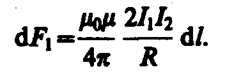(111. 3)

Рассуждая аналогично, можно показать, что сапа dF₂ с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в противоположную сторону и по модулю равна

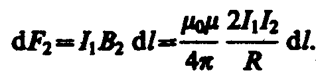(111. 4)

Сравнение выражений (111. 3) и (111. 4) показывает, что

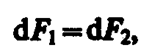
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

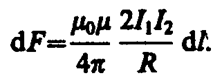(111. 5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111. 5).

§ 112. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля

Если два параллельных проводника с током находятся в вакууме (m=1), то сила взаимодействия на единицу длины проводника, согласно (111. 5), равна

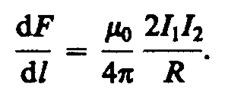(112. 1)

Для нахождения числового значения m₀ воспользуемся определением ампера, согласно

которому 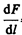=2× 10^–7 Н/м при I₁= I₂= 1 А и R = 1 м. Подставив это значение в формулу (112. 1), получим

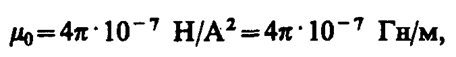
где генри (Гн) — единица индуктивности (см. § 126).

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111. 2)) запишется в виде dF=IBdl, откуда

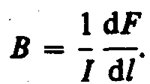
Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А:

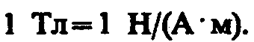
Так как m₀= 4p× 10^–7 Н/А², а в случае вакуума (m = 1), согласно (109. 3), B=m₀H, то для данного случая

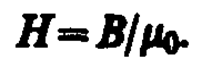
Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4p× 10^–7 Тл.

§ 113. Магнитное поле движущегося заряда

Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой

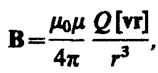(113. 1)

где r — радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис. 168).

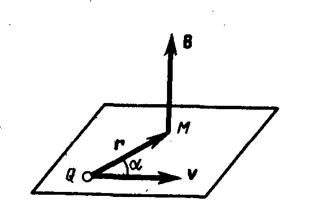
Согласно выражению (113. 1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и r, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к r.

Модуль магнитной индукции (113. 1) вычисляется по формуле

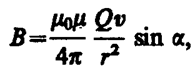(113. 2)

где a — угол между векторами v и r.

Сравнивая выражения (110. 1) и (113. 1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:

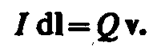
Приведенные закономерности (113. 1) и (113. 2) справедливы лишь при малых скоростях (v< < с) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.

Формула (113. 1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на —Q. Скорость v — относительная скорость, т. е. скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависит как от времени, так и от положения точки М наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.

§ 114. Действие магнитного поля на движущийся заряд

Опыт показывает, что магнитное поле действует не только на проводники с током (см. § 111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой

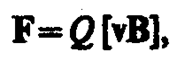(114. 1)

где В — индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q< 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда.

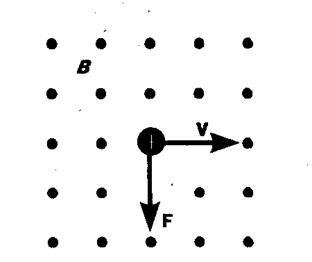
На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца (см. (114. 1)) равен

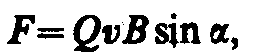
где a — угол между v и В.

Отметим еще раз (см. § 109), что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.

Так как по действию силы Лоренца можно найти модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:

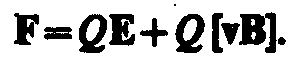
Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

§ 115. Движение заряженных частиц в магнитном поле

Выражение для силы Лоренца (114. 1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол a между векторами v и В равен 0 или p. Тогда по формуле (114. 1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия QvB=mv²/r откуда

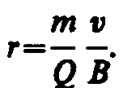(115. 1)

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

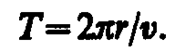
Подставив сюда выражение (115. 1), получим

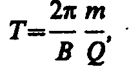(115. 2)

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v< < c). На этом основано действие циклических ускорителей заряженных частиц (см. § 116).

Если скорость v заряженной частицы направлена под углом a к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v_||=vcosa ; 2) равномерного движения со скоростью v_^=vsina по окружности в плоскости, перпендикулярной полю.

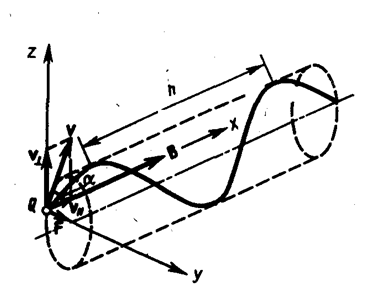
Радиус окружности определяется формулой (115. 1) (в данном случае надо заменить v на v_^=vsina). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии

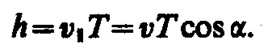
Подставив в последнее выражение (115. 2), получим

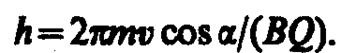
Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость v заряженной частицы составляет угол a с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.

§ 117. Эффект Холла

Эффект Холла* (1879) — это возникновение в металле (или полупроводнике) с током плотностью j, помещенном в магнитное поле В, электрического поля в направлении, перпендикулярном В и j.

* Э. Холл (1855—1938) — американский физик.

Поместим металлическую пластинку с током плотностью j в магнитное поле В, перпендикулярное j (рис. 172).

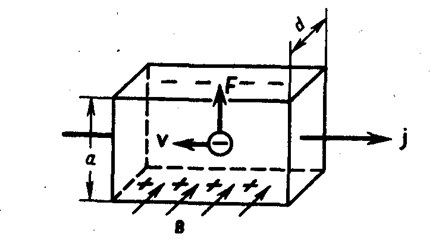
При данном направлении j скорость носителей тока в металле — электронов — направлена справа налево. Электроны испытывают действие силы Лоренца (см. § 114), которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникнет повышенная концентрация электронов (он зарядится отрицательно), а у нижнего — их недостаток (зарядится положительно). В результате этого между краями пластинки возникнет дополнительное поперечное электрическое поле, направленное снизу вверх. Когда напряженность Е_B этого поперечного поля достигнет такой величины, что его действие на заряды будет уравновешивать силу Лоренца, то установится стационарное распределение зарядов в поперечном направлении. Тогда

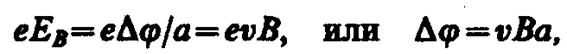
где а — ширина пластинки, Dj — поперечная (холловская) разность потенциалов.

Учитывая, что сила тока I=jS=nevS (S — площадь поперечного сечения пластинки толщиной d, п — концентрация электронов, v — средняя скорость упорядоченного движения электронов), получим

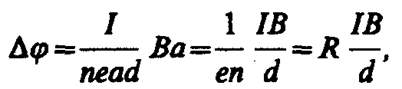(117. 1)

т. е. холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции В, силе тока I и обратно пропорциональна толщине пластинки d. В формуле (117. 1) R=1/(en) — постоянная Холла, зависящая от вещества. По измеренному значению постоянной Холла можно: 1) определить концентрацию носителей тока в проводнике (при известных характере проводимости и заряда носителей); 2) судить о природе проводимости полупроводников (см. § 242, 243), так как знак постоянной Холла совпадает со знаком заряда е носителей тока. Эффект Холла поэтому — наиболее эффективный метод изучения энергетического спектра носителей тока в металлах и полупроводниках. Он применяется также для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т. д.

§ 118. Циркуляция вектора В магнитного поля в вакууме

Аналогично циркуляции вектора напряженности электростатического поля (см. § 83) введем циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл

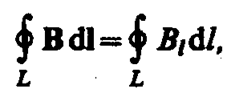
где dl — вектор элементарной длины контура, направленной вдоль обхода контура, B_l=Bcosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), a — угол между векторами В и dl.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В):

циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватываемых этим контуром:

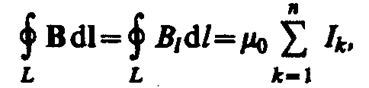(118. 1)

где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,

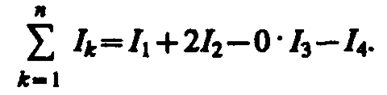
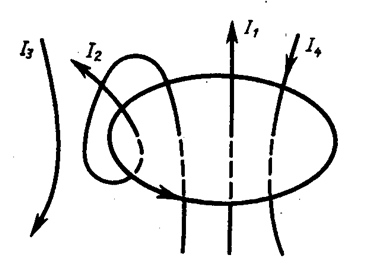
Выражение (118. 1) справедливо только для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи.

Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам (рис. 174). Представим себе замкнутый контур в виде окружности радиуса r. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна

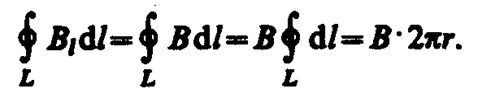
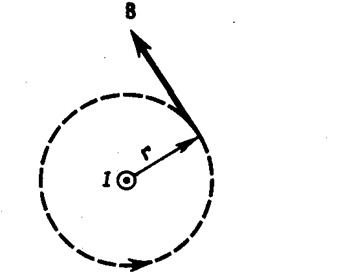
Согласно выражению (118. 1), получим В× 2pr=m₀I (в вакууме), откуда

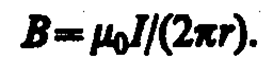
Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока, выведенное выше (см. (110. 5)).

Сравнивая выражения (83. 3) и (118. 1) для циркуляции векторов Е и В, видим, что между ними существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био — Савара— Лапласа.

§ 119. Магнитные поля соленоида и тороида

Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоида (см. рис. 162, б) показывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 175.

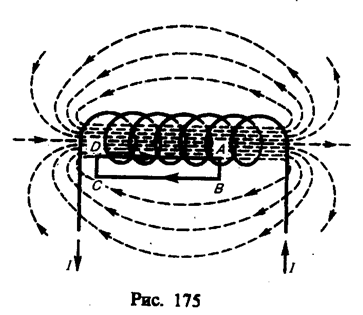
Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно (118. 1), равна

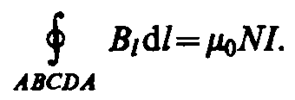
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и B_l=0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно,

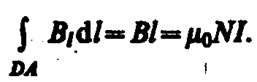(119. 1)

Из (119. 1) приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

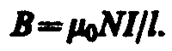(119. 2)

Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био — Савара — Лапласа; в результате получается та же формула (119. 2).

Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

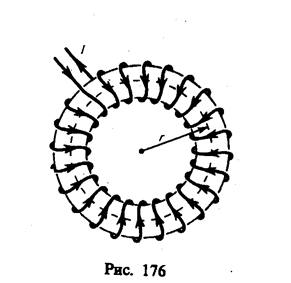
Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции (118. 1), B× 2pr=m₀NI , откуда следует, что магнитная индукция внутри тороида (в вакууме)

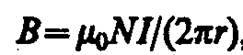
где N — число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и B× 2pr=0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).

§ 120. Поток вектора магнитной индукции. Теорема Гаусса для поля В

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная

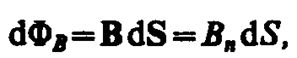(120. 1)

где B_n=В cos a —проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), dS=dSn — вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cos a (определяется выбором положительного направления нормали n). Поток вектора В связывают с контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено (см. § 109): оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции Ф_B через произвольную поверхность S равен

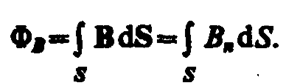(120. 2)

Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, B_n=B=const и

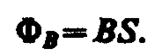
Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл× м²).

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

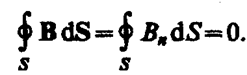(120. 3)

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные выражения (см. (120. 3), (81. 2)).

В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью m, согласно (119. 2), равна

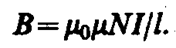
Магнитный поток сквозь один виток соленоида площадью S равен

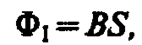
а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

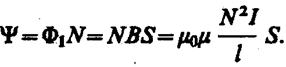(120. 4)

§ 121. Работа по перемещению проводника и контура с током в магнитном поле

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результиру­ющего колебания А равна сумме амплитуд складываемых колебаний; 6 страница

1) j2—j1 = ±2mp (т=0, 1, 2, .), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 6 страница