- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
o It is a star. o It is a cycle. o It is a complete graph
o It is a star
o It is a cycle
o It is a complete graph
· None of these
108. Consider the complement of this graph: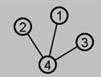 
.
· It contains a subgraph which is a cycle with three edges.
o It is a cycle with four edges
o It is a star with three edges
o It is a star with four edges
o It is a path with four edges
109. Consider the planar code 00110011
o It is the planar code of an unlabeled tree with 4 nodes
o It is the planar code of an unlabeled tree with 5 nodes
o It is the planar code of an unlabeled tree with 8 nodes
o It is the planar code of an unlabeled tree with 9 nodes
· There is no tree which has this planar code
110. Consider the planar code 11001100
o It is the planar code of an unlabeled tree with 4 nodes
· It is the planar code of an unlabeled tree with 5 nodes
o It is the planar code of an unlabeled tree with 8 nodes
o It is the planar code of an unlabeled tree with 9 nodes
o There is no tree which has this planar code
111. Consider the planar code 11001010
· It is the planar code of an unlabeled tree with 4 edges
o It is the planar code of an unlabeled tree with 5 edges
o It is the planar code of an unlabeled tree with 8 edges
o It is the planar code of an unlabeled tree with 9 edges
o There is no tree which has this planar code
112. Consider the planar code 11011010
o It is the planar code of an unlabeled tree with 4 edges
o It is the planar code of an unlabeled tree with 5 edges
o It is the planar code of an unlabeled tree with 8 edges
o It is the planar code of an unlabeled tree with 9 edges
· There is no tree which has this planar code
113. How many cut edges does graph K have?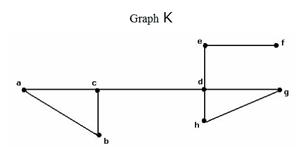 
o 0
o 1
o 2
· 3
o 4
114. 4 How many leaves does graph K have?
o 0
· 1
o 2
o 3
o 4
115. Which is a cut edge of graph K?
o ac
o ab
· cd
o cb
o dh
116. Which node is a leaf of graph K?
o a
o b
o d
· f
o g
117. What is the planar code for this graph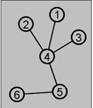 
if you start just above node 6 (the root) and walk to the right?
· 1110101000
o 65434142456
o 1100110010
o 0001010111
o 65424143456
118. What is the planar code for this graph 
if you start just above node 6 (the root) and walk to the right?
· 1111100000
o 111111000000
o 654213
o 65421312456
o None of these
119. What is the planar code for this graph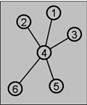 
if you start just above node 6 (the root) and walk up and to the right?
o 64241434546
o 0010101011
o 642135
· 1101010100
o None of these
120. 
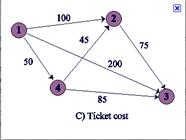What is the least amount you need to spend on tickets to visit the other three cities assuming you start in #1?
· 170
o 180
o 190
o 200
o None of these
121. For this graph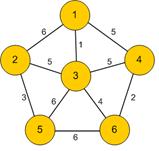 
, what is the total distance of all the edges in the minimal spanning tree?
· 15
o 16
o 17
o 18
o None of these
122. If this graph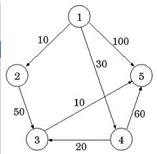 
shows the costs (in millions of Tenge) of connecting various nodes, what is the cost of the minimal (cheapest) spanning tree?
o 60 million KZT
· 70 million KZT
o 80 Million KZT
o 90 Million KZT
o None of these
123. 
What is the length in miles of the shortest spanning tree connecting these cities in Wisconsin, USA?
o 442 miles
o 289 miles
o 263 miles
· 261 miles
o None of these
124. Which of the following two statements are true? 1) All trees are connected graphs. 2) All trees contain have no cycles.
o Both are false
o 1) is true; 2) is false
o 1) is false; 2) is true
· Both are true
o The statements contradict each other so at least one of them must be false.
125. Is there a Hamiltonian cycle in a graph with m edges and n nodes, exactly three of which have odd degree?
o Yes, always
o No, never
o Maybe; it depends upon the details of the graph
· No such graph exists
o This is still an unsolved problem
126. How many bits does it take to store the optimal spanning tree of a graph on 63 nodes using an adjacency matrix? (Remember, we do not need to store the diagonal or the lower rectangle of the matrix, – just the part above the diagonal).
o 3969
o 3906
o 15624
· 1953
o None of these
127. How many bits does it take to store the optimal spanning tree of a graph on 63 nodes using the Prьfer Code?
o 61
o 62
· 366
o 372
o None of these
128. How many bits does it take to store the optimal spanning tree of a graph on 63 nodes using the Father Code?
o 61
o 62
· 372
o 434
o None of these
129. For which graph is this the adjacency matrix: 
? (The rows and columns are labeled 1, 2, 3, 4 – there is no 0 row or column in this problem).
· This is the adjacency matrix for a path of length 3.
o This is the adjacency matrix for a cycle of length 4.
o This is the adjacency matrix for a star with 3 arms.
o This is the adjacency matrix for the complete graph on 4 nodes.
o None of these
130. What is the adjacency matrix for this star graph: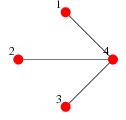 
?
o
o 
· 
o 
o None of these
131. For which graph is this the adjacency matrix: 
? (The rows and columns are labeled 1, 2, 3, 4 – there is no 0 row or column in this problem).
o This is the adjacency matrix for a path of length 3.
· This is the adjacency matrix for a cycle of length 4.
o This is the adjacency matrix for a star with 3 arms.
o This is the adjacency matrix for the complete graph on 4 nodes.
o None of these
132. What is the adjacency matrix for this complete graph: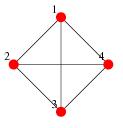 
?
o
·
o
o
o None of these
133. This soccer ball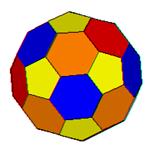 
has 12 regular pentagons (five edges) and 20 regular hexagons (six edges). How many vertices does it have?
o 45
o 54
· 60
o 72
o None of these
134. This soccer ball 
consists of 92 faces – 12 regular pentagons (five edges), 20 hexagons (six edges) and 60 triangles (three edges). How many vertices does it have?
o 45
o 54
o 60
· 90
o None of these
135. This polyhedron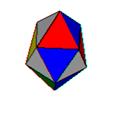 
is made of 16 equilateral triangles. How many vertices does it have?
o 24
o 18
o 12
· 10
o None of these
136. This polyhedron is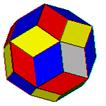 
built of 30 congruent rhombuses (four sided polygons with sides of equal length). How many vertices does it have?
o 24
· 32
o 36
o 48
o None of these
137. A planar graph has 8 regions and 9 vertices. How many edges does it have?
o 19
o 17
· 15
o 13
o None of the above
138. A planar graph has 21 edges and 14 vertices. How many regions does it have?
o 37
o 33
o 7
o 5
· None of the above
139. A planar graph has 9 edges and 5 regions. How many vertices does it have?
o 12
o 16
o 7
· 6
o None of the above
140. Use the Tree Shortcut Algorithm to find a Traveling Salesman tour around this minimal spanning tree (bold):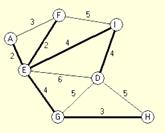 
. Start just below the H and move to the left. How long is the tour?
o 23
o 24
o 25
· 26
o None of these
141. Starting just above node 0 and moving up and to the right, use the Tree Shortcut Algorithm to find a Traveling Salesman tour around this minimal spanning tree (red):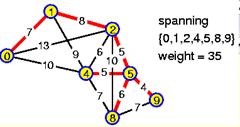 
. How long is the tour?
o 36
· 48
o 40
o 38
o None of these
142. What is the third edge built in this graph 
starting from node D using the Greedy Algorithm?
o BD
· BA
o AE
o CD
o None of these
143. Which of the following two statements are true? 1) If a graph has a walk connecting two points it also has a path connecting the same two points. 2) If a graph is connected then it is a tree.
o Both are true
o Both are false
· 1) is true; 2) is false
o 2) is true; 1) is false
o None of the above
144. Which statement is true?
o Every graph with at least two nodes has a node of degree one.
o Every graph with at least two nodes has two nodes of degree one.
o Every tree with at least three nodes has at least three nodes of degree one.
· Every tree with at least two nodes has at least two nodes of degree one.
o There exists a tree with exactly one node of degree one.
145. If you delete an edge of a tree what happens?
· The resulting graph is always disconnected.
o The resulting graph may or may not be disconnected depending on the details of the tree structure.
o The remaining graph will always contain a cycle.
o One cycle of the tree will be broken.
o None of these
146. What is the Prьfer Code of this labeled tree?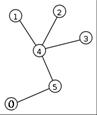 
(Assume that the root is 0. )
· 4445
o 44450
o 12345
o 5444
o None of these
147. If the Prьfer code of a tree is 01014, what is the top row (the row of sons)? (Assume that the root is 0. )
o 23501
o 253614
· 235614
o 23516
o None of these
148. What is the Prьfer Code of this labeled tree?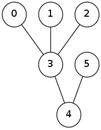 
(Assume that the root is 0. )
o 12540
o 54321
o 054123
o 12543
· None of these
149. If the Prьfer code of a tree is 3333, what is the top row (the row of sons)? (Assume that the root is 0. )
· 12453
o 0124
o 0000
o 01243
o None of these
150. What is the Father Code of this labeled tree? (Assume that the root is 0. )
o 4445
· 44450
o 054312
o 5444
o None of these
151. What is the Father Code of this labeled tree? (Assume that the root is 0. )
· 33034
o 54321
o 054123
o 12543
o None of these
152. If the Father Code of a tree is 510101, what is the degree of the node 1? (Hint – add the top row and then draw the tree. ) Assume that the root is 0.
o 1
o 2
o 3
· 4
o None of these
153. If the Father Code of a tree is 0011220, what is the degree of the node 2? (Hint – add the top row and then draw the tree. ) Assume that the root is 0.
o 1
o 2
· 3
o 4
o None of these
154. If the Prьfer code of a tree is 4321, what is the top row (the row of sons)? Assume that the root is 0.
o 5432
o 0432
o 04321
· 54321
o None of these
155. If the Prьfer code of a tree is 3020, what is the Father Code? (Find the row of sons, draw the tree and determine its Father Code). Assume that the root is 0.
· 30020
o 302
o 1342
o 03020
o None of these
156. What is the Prьfer code of a star on five nodes with the root 0 at the center?
o 1234
o 12340
o 0000
o 00000
· None of these
157. What is the Father code of a star on five nodes with the root 0 at the center?
o 1234
o 12345
· 0000
o 00000
o None of these
158. If you add an edge to a tree (without adding a vertex) what happens?
o The resulting graph remains disconnected.
o You may or may not create a cycle depending on the details of the tree structure.
· The resulting graph will always contain a cycle.
o The resulting graph will still be a tree.
o None of these
159. What is the length of the shortest circuit on this lattice of dots 
assuming that the rows and columns are separated by 2cm each?
o 18 cm
o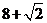 
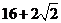cm
· 
cm
o 16 cm
o None of these
160. What is the length of the shortest circuit on this lattice of dots 
assuming that the rows and columns are separated by 1cm each?
o 13 cm
· 12 cm
o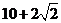 
cm
o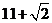 
o None of these
161. What is the length of the shortest circuit on this lattice of dots 
assuming that the rows and columns are separated by 3cm each?
o 46 cm
o 45 cm
o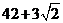 
cm
o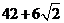 
· None of these
162. Try to draw a graph with the following degrees for its five nodes: 1, 1, 1, 1, 2? Which statement is true?
o Such a graph has two edges and is connected
o Such a graph has three edges and is connected
o Such a graph has two edges and is not connected
· Such a graph has three edges and is not connected
o No such graph exists
163. Try to draw a graph with the following degrees for its five nodes: 2, 2, 2, 2, 2? Which statement is true?
o The graph is a path with five edges
· The graph is a cycle with five edges
o The graph is a path with ten edges
o The graph is a cycle with ten edges
o No such graph exists
164. Try to draw a graph with the following degrees for its five nodes: 1, 1, 1, 1, 1? Which statement is true?
o Such a graph has two edges and is connected
o Such a graph has three edges and is connected
o Such a graph has two edges and is not connected
o Such a graph has three edges and is not connected
· No such graph exists
165. Try to draw a graph with the following degrees for its five nodes: 0, 1, 2, 3, 4? Which statement is true?
o Such a graph has six edges
o Such a graph has five edges
o Such a graph has four edges
o Such a graph has three edges
· No such graph exists
166. Consider this unlabeled tree: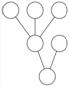 
. Which of the following unlabeled trees is it the same as (isomorphic to)?
o 
o 
· 
o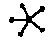 
o 
167. Consider this unlabeled tree: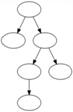 
. Which of the following unlabeled trees is it the same as (isomorphic to)?
o
·
o
o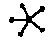
o
168. Consider this unlabeled tree: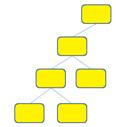 
. Which of the following unlabeled trees is it the same as (isomorphic to)?
o
o
o
o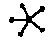
·
169. In this tree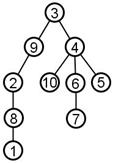 
, assume the node labeled 3 is the root. How many sons does node 4 have?
o 0
o 1
o 2
· 3
o 4
170. In this tree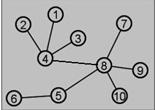 
assume the node labeled 4 is the root. Which node is the father of node 8?
· Node 4
o Node 5
o Node 10
o Node 9
o Node 7
171. In building the minimal spanning tree (thick lines are already built) for this graph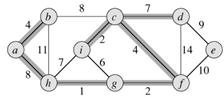 
, which edge should be built next?
o The edge connecting i and g.
o The edge connecting i and h.
o The edge connecting b and c.
· The edge connecting d and e.
o None of these – the spanning tree is already finished.
172. One six-sided die is rolled. Let E be the event that an even number {2, 4, 6} is face up. Let O be the event that an odd number is face up {1, 3, 5}. Are these events independent? Are they mutually exclusive?
o They are both independent and mutually exclusive.
o They are independent and not mutually exclusive.
· They are not independent but are mutually exclusive.
o They are neither independent nor mutually exclusive.
o None of these.
173. One six-sided die is rolled. Let E be the event that an even number {2, 4, 6} is face up. Let L be the event that a larger than average number is face up {4, 5, 6}. Are these events independent? Are they mutually exclusive?
o They are both independent and mutually exclusive.
o They are independent and not mutually exclusive.
o They are not independent but are mutually exclusive.
· They are neither independent nor mutually exclusive.
o None of these.
174. One six-sided die is rolled. Let E be the event that an even number {2, 4, 6} is face up. Let T be the event that a multiple of three is face up {3, 6}. Are these events independent? Are they mutually exclusive?
o They are both independent and mutually exclusive.
· They are independent and not mutually exclusive.
o They are not independent but are mutually exclusive.
o They are neither independent nor mutually exclusive.
o None of these.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|