- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
o It is a tree
1. What is the next step in finding gcd(101, 16) by the Euclidean algorithm?
o =gcd(101, 6)
o =gcd(6, 16)
o =gcd(101, 5)
· =gcd(5, 16)
o none of these
2. What is the next step in finding gcd(76, 14) by the Euclidean algorithm?
· =gcd(6, 14)
o =gcd(5, 14)
o =gcd(76, 5)
o =gcd(76, 6)
o none of these
3. What is the next step in finding gcd(96, 16) by the Euclidean algorithm?
o gcd(6, 16)
o =6
o =gcd(0, 6)
o =0
· none of these
4. What is the next step in finding gcd(87, 86) by the Euclidean algorithm?
o =gcd(87, 1)
o =gcd(87, 86)
· =gcd(1, 86)
o =1
o none of these
5. What is gcd(24, 8)?
o 3
· 8
o 24
o 4
o none of these
6. What is gcd(36, 7)?
· 1
o 0
o 5
o 7
o none of these
7. What is gcd(42, 9)?
o 9
o 33
o 6
o 4
· none of these
1. What is gcd(500, 225)?
o 2
· 25
o 50
o 275
o none of these
2. If x & y are positive integers and x is relatively prime to y, and x < y, what is gcd(x, y)?
o 0
· 1
o x
o y
o not enough information
3. If x & y are positive integers and if x is prime and y is not prime, what is gcd(x, y)?
o 0
o 1
o x
o y
· not enough information
4. If x & y are distinct positive integers and both are prime, what is gcd(x, y)?
o 0
· 1
o x·y
o x+y
o not enough information
5. Consider the two statements: 1) It is possible using current technology to quickly generate a 200 digit prime number which starts with the digits 123; 2) It is possible using current technology to factor any 200 digit composite number in a few seconds.
o Statement 1) is true, 2) is true.
· Statement 1) is true, 2) is false.
o Statement 1) is false, 2) is true.
o Statement 1) is false, 2) is false.
o Only the CIA and KGB know the answers.
6. Is there an Eulerian walk in a graph which has six nodes, exactly three of which have odd degree?
o Yes
o No
o Maybe – it depends on the other details of the graph.
· No such graph exists
o We don’t know - this is still an unsolved problem.
7. Is there an Eulerian walk in a graph which has seven nodes, exactly two of which have odd degree?
· Yes
o No
o Maybe – it depends on the other details of the graph.
o No such graph exists.
o We don’t know - this is still an unsolved problem.
8. Is there a closed Eulerian walk in a graph which has eight nodes, all of even degree?
· Yes
o No
o Maybe – it depends on the other details of the graph.
o No such graph exists.
o We don’t know - this is still an unsolved problem.
9. Is there an Eulerian walk in a graph which has 43 nodes, exactly six of which have odd degree?
o Yes
· No
o Maybe – it depends on the other details of the graph.
o No such graph exists.
o We don’t know - this is still an unsolved problem.
10. Are there Eulerian walks in these two graphs? (Nodes with even degree are black. )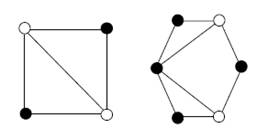 
· Yes for both
o No for both
o Yes for the one on the left only
o Yes for the one on the right only
o This is still an unsolved problem.
11. Consider possible Eulerian walks in this graph. Which statement below is true?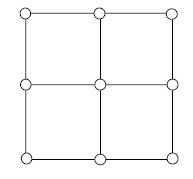 
o There are Eulerian walks and they are all closed.
o There are Eulerian walks and some are closed and some are open.
· There are no Eulerian walks.
o More information is needed.
o This is still an unsolved problem.
12. Consider possible Eulerian walks in this graph. Which statement below is true?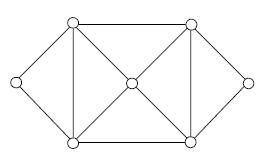 
· There are Eulerian walks and they are all closed.
o There are Eulerian walks and some are closed and some are open.
o There are Eulerian walks and none are closed.
o There are no Eulerian walks.
o This is still an unsolved problem.
13. Consider possible Eulerian walks in this graph. Which statement below is true?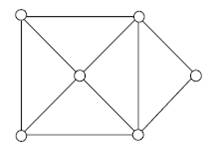 
o There are Eulerian walks and they are all closed.
o There are Eulerian walks and some are closed and some are open.
· There are Eulerian walks and none are closed.
o There are no Eulerian walks.
o This is still an unsolved problem.
14. Find 519 mod 7.
o 1
o 2
o 3
o 4
· 5
15. Find 527 mod 6.
o 1
o 2
o 3
o 4
· 5
16. Find 716 mod 10
· 1
o 3
o 5
o 7
o 9
17. Find 97 mod 11
o 1
o 2
o 3
· 4
o 5
18. In RSA public key cryptography, which keys are used to send a message from Bob to Alice?
o Bob’s private key and Alice’s public key.
o Bob’s public key and Alice’s private key.
· Alice’s public and private keys.
o Bob’s public key and Alice’s two keys.
o All four keys are used.
19. How many distinct ways are there to order the letters of the word " Mississippi”?
o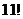 
o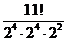 
· 
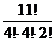
o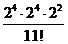 
o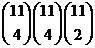 
20. How many ways can nine friends be divided into three groups of three?
o 27
o 140
· 280
o 1680
o None of these
21. How many ways can six friends be divided into three groups of two (three pairs)?
· 15
o 20
o 45
o 90
o None of these
22. How many ways can six friends be divided into two groups of three?
o 6
· 10
o 20
o 90
o None of these
23. How many different ways can the first round of a chess tournament of the top four players be started? (It matters if a player has the white pieces or the black ones. )
o 6
o 8
o 12
o 32
· None of these
24. Six ladies are to be grouped into three pairs to play on courts A, B, and C. In how many ways can this be done? (The same three pairs of girls playing on different courts counts as a different grouping – order matters).
o 18
o 24
o 45
· 90
o None of these
25. How many ways can two skating pairs (one man with one woman) be chosen for the Olympic games from the top four men and top five women? (Order of the pairs is not counted).
o 24
o 60
o 90
· 120
o None of these
26. A committee of three is to be chosen from six people. One will be named the chairman. How many possible committee & chairman combinations are there? (Given which people are on the committee, there are still different committees – depending on who the chairman is).
o 12
o 24
o 45
· 60
o None of these
27. A class of five boys and ten girls needs to choose two class representatives – a president and vice president. They must choose one boy and one girl for these two offices. How many ways can this be done?
o 15
o 30
o 50
· 100
o None of these
28. How many ways can you choose a dozen (i. e. 12) pastries from a shop which sells four different kinds if you need to buy at least two of each kind?
o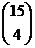 
o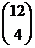 
o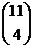 
o 
· None of these
29. How many ways can you choose a dozen (i. e. 12) pastries from a shop which sells four different kinds if you need to buy at least one of each kind?
o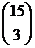 
o 
o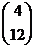 
· 
o None of these
30. How many ways can you choose a dozen (i. e. 12) pastries from a shop which sells four different kinds? (There is no requirement that you buy one of each kind. )
o
o
o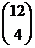
o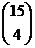
· None of these
31. Use the Binomial Theorem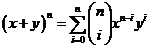 
to find the coefficient of the 
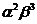term in the expansion of 
.
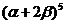o 5
o 10
o 20
· 80
o There is no 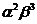term in the expansion.
32. Which is the correct expansion of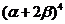 
? The Binomial Theorem may be helpful: .
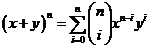o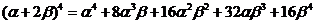 
· 
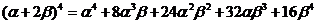
o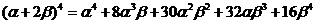 
o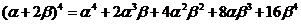 
o None of these.
33. What is the sum of the coefficients in the expansion of 
? The Binomial Theorem may be helpful: .
o 0
o 
o 16
· 32
o None of these
34. What is the sum of the coefficients in the expansion of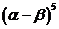 
? The Binomial Theorem may be helpful: .
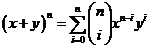· 0
o
o 16
o 32
o None of these
35. Which of these is not true? (Think about Pascal’s Triangle. )
o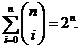 
o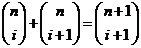 
o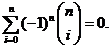 
o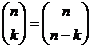 
· All of these are true
36. Which of the following expresses the identity where the sum of two consecutive numbers in Pascal’s Triangle equals the number in the row below and between them?
o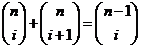 
· 
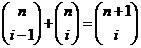
o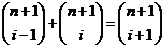 
o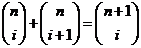 
o None of these
37. What is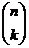 
equal to?
o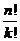 
o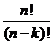 
o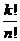 
o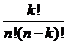 
· None of these
38. What is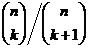 
?
o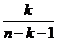 
o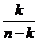 
· 
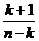
o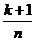 
o None of these
39. Which of the following expresses the fact that Pascal’s triangle is symmetric about the vertical center line? (The left side of Pascal’s Triangle is a reflection of the right side. )
o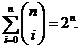
o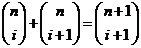
o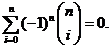
·
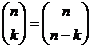
o None of these
40. What is the sum of the entries in the tenth row (i. e. the row that begins {1, 10, 45, …} in Pascal’s Triangle?
o 10!
o 1000
o 10! /(2! ·8! )
· 210
o None of these
41. For the Fibonacci numbers which obey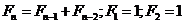 
, what is 
?
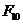o 8
o 13
o 21
o 34
· 55
42. What is the characteristic equation for the Fibonacci recurrence relation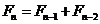 
?
o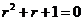 
o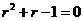 
· 
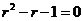
o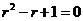 
o None of these
43. What are the initial conditions which give the Fibonacci numbers as the unique solution of the Fibonacci recurrence relation ?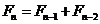
o Given that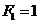 
.
· Given that 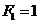and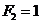 
.
o No initial conditions are necessary – the recurrence relation already determines the Fibonacci numbers.
o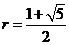 
.
o None of these
44. For the Fibonacci numbers which obey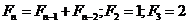 
, what is 
?
o 0
· 1
o -1
o -2
o 2
45. In a class of 100 students, 17 are good in math and 27 are good in English. Only 4 are good in both subjects. How many students are not good in either English or math?
· 60
o 40
o 56
o 44
o None of these
46. Let A2, A3, and A5 be the set of multiples of 2, 3, and 5 up to 60, i. e.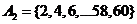 
; 
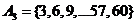; and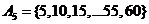 
. How many of the first 60 positive integers are in at least one of these three sets? You will need to use 
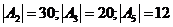and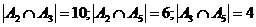 
. And you need to find 
.
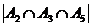o 16
· 44
o 24
o 48
o None of these
47. Given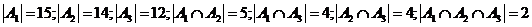 
; what is 
?
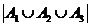o 26
o 27
o 28
o 29
· None of these
48. In a class of 10 students, 5 are good in math, 4 are good in English and 3 are good in history. 2 are good in both math and English, 2 are good in both English and history, and 1 is good in both math and history. 0 are good in all three subjects. How many are good in at least one subject?
o 1
o 3
o 5
· 7
o 9
49. Suppose there are 15 cards – five blue, five green, and five red. How many subsets of four cards have at least one color missing? Hints: Let Ab={subsets of four cards without any blue cards}; Ag={subsets of four cards without any green cards}; Ar={subsets of four cards without any red cards}. Each of these have cardinality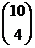 
. The question asks for 
.
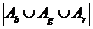o 
o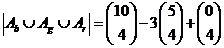 
o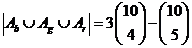 
· 
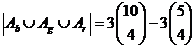
o None of these
50. Eleven bullets hit a 20cm x 50cm rectangular target. Let d be the distance between the pair which hit closest to each other. Which is the strongest statement which must be true:
o d< 10cm
· d< 15cm
o d< 20cm
o d< 25cm
o None of these
51. There are six gas stations on a 500km long road across the Kara Kum desert. Let d be the distance between the pair of gas stations which are closest together. Which is the strongest statement which must be true:
o d< 501km
o d< 251km
o d< 126km
· d< 101km
o d< 84km
52. Suppose a company sells 27 flavors of ice cream. On one day they serve 123 children. Which is the strongest statement which must be true:
o At least two children had the same flavor of ice cream.
o At least three children had the same flavor of ice cream.
o At least four children had the same flavor of ice cream.
· At least five children had the same flavor of ice cream.
o At least six children had the same flavor of ice cream.
53. Ten pioneers want to build their houses in a 36km2 square region. They each want to stay as far as possible away from all of their neighbors. Which is the strongest true statement?
o One of them must have a neighbor closer than 2km away.
· One of them must have a neighbor closer than 3km away.
o One of them must have a neighbor closer than 4km away.
o One of them must have a neighbor closer than 5km away.
o One of them must have a neighbor closer than 5km away.
54. Suppose that all snakes in one region are between 20cm and 35cm long. Without hurting the snakes, we want to find a pair of snakes whose lengths are no more than 0. 5cm apart. How many snakes must we measure to be guaranteed of success?
o 15
o 16
o 30
· 31
o 2 - just cut one of the two snakes so they are the same length.
55. Two six-sided dice are rolled. What is the probability that the difference of the two numbers is 0 or 1?
o 12/36=1/3
o 13/36
o 14/36=7/18
o 15/36=5/12
· 16/36=4/9
56. Two six-sided dice are rolled. What is the probability that the product of the two numbers is more than 19?
o 10/36=5/18
o 9/36=1/4
· 8/36=2/9
o 7/36
o 6/36=1/6
57. 
A 20-sided die numbered 1, 2, 3, …, 20 and an 8-sided die numbered 1, 2, 3, …, 8 are rolled. What is the probability that the two numbers are the same?
o 1/4
o 1/8
o 1/10
o 1/12
· 1/20
58. 
A 4-sided die and a 6-sided die are rolled. What is the probability that the sum of the two numbers is 7?
· 1/6
o 1/8
o 1/10
o 1/12
o 0
59. Which of these is a non-linear recurrence equation?
o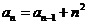 
· 
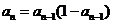
o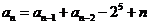 
o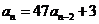 
o All of them are non-linear
60. Which of these is a non-homogeneous linear recurrence relation?
o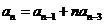 
o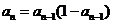
o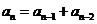 
· 
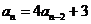
o None of them
61. Which of these is a homogeneous linear recurrence relation with constant coefficients?
o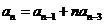
o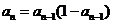
· 
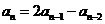
o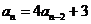
o None of them
62. Which of these is a linear recurrence relation with constant coefficients?
o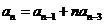
o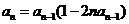 
· 
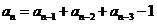
o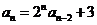 
o None of them
63. Suppose that the characteristic equation of a homogeneous linear recurrence equation with constant coefficients has roots 3 and 4. What is the form of the general solution of this equation?
o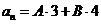 
o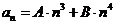 
· 
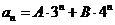
o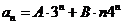 
o None of them
64. What is the order of the recurrence relation ?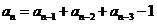
o -1
o 0
o 1
o 2
· 3
65. How many initial conditions do we need to determine a unique solution for the recurrence relation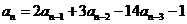 
?
o 0
o 1
o 2
· 3
o 4
66. Suppose that the characteristic equation of a homogeneous linear recurrence equation with constant coefficients has roots 3, 3, and 4. What is the form of the general solution of this equation?
o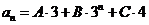 
· 
o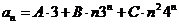 
o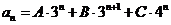 
o None of them
67. What form should we try in order to find a particular solution for the non-homogeneous recurrence relation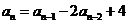 
?
o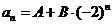 
o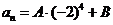 
o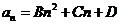 
· 
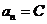
o None of them
68. What form should we try in order to find a particular solution for the non-homogeneous recurrence relation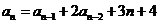 
?
· 
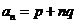
o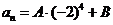
o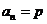 
o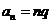 
o None of them
69. What form should we try in order to find a particular solution for the non-homogeneous recurrence relation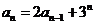 
?
o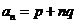
o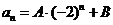 
· 
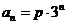
o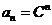 
o None of these
70. Suppose we need to solve the non-homogeneous recurrence relation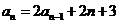 
. We try a particular solution of the form 
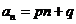. After substituting and some algebra we arrive at 
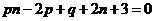. Solve for p & q.
o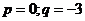 
o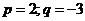 
· 
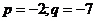
o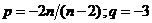 
o None of these
71. Suppose we are solving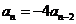 
with initial conditions 
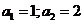. The roots of the characteristic equation are 
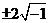. Which is true:
o No solution exists.
o A unique solution exists, but it will include imaginary numbers.
o There are two solutions to the problem and both include imaginary numbers.
· The solution exists and is a real number for every integer n.
o All of these statements, including this one, are false.
72. Which statement is always true:
o If p | (14p – 14) then p is prime.
· If p is prime then p | 14p – 14.
o If p and 14 are relatively prime, and p | 14p – 14, then p is a base 14 pseudoprime.
o If p and 14 are relatively prime then p | 14p − 14.
o None of these are true.
73. Which statement is always true:
o If p | (14p – 14) then p is prime.
o If p and 14 are relatively prime, and p | 14p− 1 – 1, then p is prime.
o If p and 14 are relatively prime, and p | 14p− 1 – 1, then p is a base 14 pseudoprime.
· If p is a prime and 14 is an integer not divisible by p, then p | 14p− 1 − 1.
o None of these are true.
74. With modern computers and the Miller-Rabin test we can quickly
o test whether a 200 digit number is prime or not with absolute certainty.
· test whether a 200 digit number is prime or not with “almost” absolute certainty.
o find at least two prime factors of any 200 digit number that fails the primality test.
o find the complete unique prime factorization of any 200 digit number that fails the primality test.
o none of these above are true
75. We are compressing the file PPCPCPCCCPCPCCCPCPCCCPCCCCCPC# with the LZW algorithm. So far we have encrypted the first three (colored) letters. Which are the four entries of the next line in the compression process?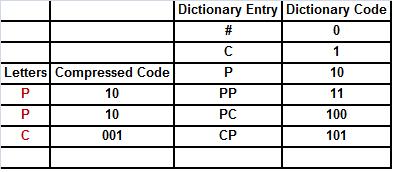 
o P; 010; PC; 100
o P; 010; PC; 110
· PC; 100; PCP; 110
o PCP; 110; PCP; 100
o None of these.
76. We are compressing the file AAABAAABAAB# with the LZW algorithm. So far we have encoded the first six (colored) letters. What is the next dictionary entry and code?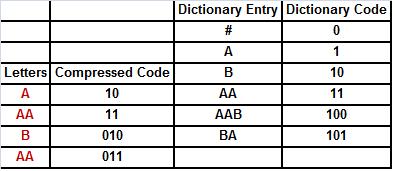 
· AAA; 110
o ABA; 102
o AAB; 100
o AB; 110
o None of these.
77. We are compressing the file ABABABAABAAABAABABA# with the LZW algorithm. So far we have encoded the first fifteen (colored) letters. What is the next line of entries?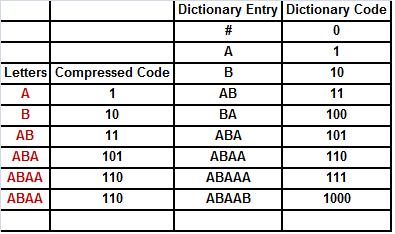 
o BA; 100; BAB; 1001
o ABA; 101; ABAB; 1001
o BAB; 0101; BABA; 1001
· BA; 0100; BAB; 1001
o None of these.
78. We are decompressing the file 0110100100011# with the LZW algorithm. So far we have decrypted the first seven (colored) bits. Which are the four entries of the next line in the decompression process?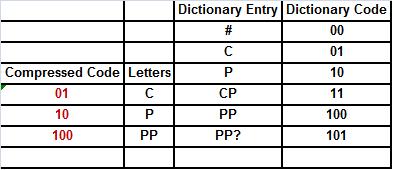 
o 0100; PP; PP?; 110
o 001; C; C?; 110
· 100; PP; PP?; 110
o 10; P; P?; 110
o None of these.
79. We are decompressing the file 0110100010011# with the LZW algorithm. So far we have decrypted the first seven bits. How do we complete the dictionary entry “PP? ” and what is/are the next letter(s) to be decompressed?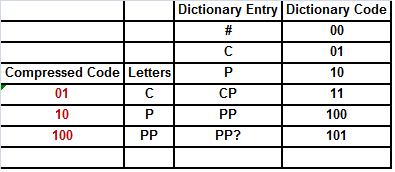 
o The dictionary entry is PPC and the next letter decompressed is C
o The dictionary entry is PPC and the next letters decompressed are PC
o The dictionary entry is PPP and the next letter decompressed is C
o The dictionary entry is PPP and the next letters decompressed are PC
· The dictionary entry is PPP and the next letter decompressed is P
80. We are decompressing the file 0110011010110# with the LZW algorithm. So far we have decrypted the first four (colored) bits. What are the four entries in the next row?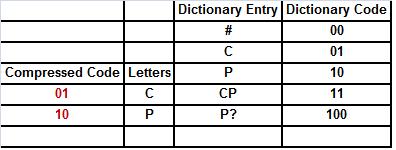 
o 01; C; C?; 101
o 11; CP; CP?; 101
· 011; CP; CP?; 101
o 110; CP; CP?; 101
o None of these
81. Suppose you have a message m you want to send to a friend (Jackie Chan) using RSA. You have Mr. Chan’s public key e and private key d, and the product of his two large primes, n. What calculation is performed to encrypt the message?
o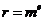 
· 
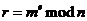
o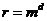 
o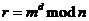 
o You cannot encrypt the message without using your own keys.
82. Suppose Borat encrypts a message m using RSA. He sends you the encrypted message, r. How do you decrypt it? You have your own public key e, private key d, and the product of your two large primes, n.
o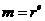 
o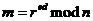 
o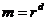 
· 
o You cannot encrypt the message without using Borat’s keys.
83. You want to set up an RSA encryption system using the primes 7& 11. You choose your public key to be e=11, knowing that it is relatively prime to (7-1)·(11-1)=60. Now you need to find your private key d, using the Euclidean algorithm to find u such that 1=u·11+v·60. Then d=u mod 60. What is d?
o d=3
o d=9
o d=19
o d=29
· none of these
84. Solve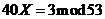 
.
o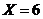 
· 
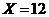
o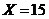 
o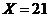 
o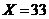 
85. Solve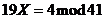 
.
o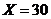 
o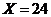 
o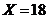 
o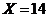 
· 
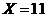
86. Solve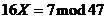 
.
o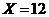
o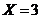 
·
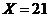
o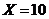 
o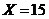
87. Solve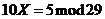 
.
o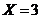
o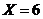
o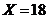
o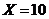
· None of these
88. Solve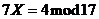 
.
·
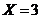
o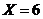
o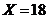
o
o None of these
89. How many connected components does this graph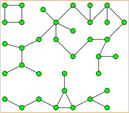 
consist of?
o 1
o 2
· 3
o 4
o 5
90. Consider 
the complete graph on 6 nodes. Which of the following statements is true?
o It has 30 edges and each of its vertices has degree 6
o It has 15 edges and each of its vertices has degree 6
o It has 30 edges and each of its vertices has degree 5
· It has 15 edges and each of its vertices has degree 5
o None of these
91. How many connected components are there in this graph?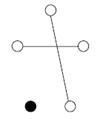 
o 0
o 1
o 2
· 3
o None of these
92. How many connected components are there in this graph?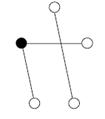 
o 0
o 1
· 2
o 3
o None of these
93. A tree has 17 nodes. How many edges does it have?
o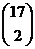 
o 17
· 16
o 18
o It depends upon the tree
94. A tree has n edges. How many nodes does it have?
o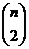 
o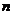 
· 
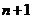
o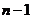 
o It depends on the tree
95. A tree has 19 edges. How many nodes does it have?
· 20
o 19
o 18
o 
o It depends upon the tree
96. A tree has n nodes. How many edges does it have?
o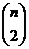
o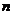
o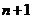
·
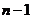
o It depends on the tree
97. Let n be the number of labeled trees on six nodes. Which is true:
o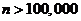 
o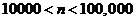 
· 
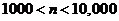
o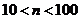 
o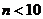 
98. How many labeled trees are there on five nodes?
o 5! =120
o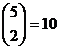 
o 54=625
o 52=25
· None of these
99. Consider these two statements for any positive integer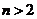 
: 1) The number of labeled trees on n nodes is 
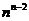; 2) There are more labeled trees than unlabeled trees.
· Both 1) and 2) are true
o 1) is true while 2) is false
o 1) is false but 2) is true
o Both 1) and 2) are false
o 1) is true but the truth of 2) depends upon the value of n.
100. Consider these two statements for any positive integer 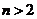: 1) The number of unlabeled trees on n nodes is 
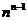; 2) There are more labeled trees than unlabeled trees.
o Both 1) and 2) are true
o 1) is true while 2) is false
· 1) is false but 2) is true
o Both 1) and 2) are false
o 1) is true but the truth of 2) depends upon the value of n.
101. Consider these two statements for any positive integer 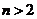: 1) The number of unlabeled trees on n nodes is less than 
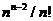; 2) There are more unlabeled trees than labeled trees.
o Both 1) and 2) are true
o 1) is true while 2) is false
o 1) is false but 2) is true
· Both 1) and 2) are false
o 1) is true but the truth of 2) depends upon the value of n.
102. Consider these two statements for any positive integer 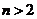: 1) The number of unlabeled trees on n nodes is 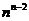; 2) There are more unlabeled trees than labeled trees.
o Both 1) and 2) are true
o 1) is true while 2) is false
o 1) is false but 2) is true
· Both 1) and 2) are false
o 1) is true but the truth of 2) depends upon the value of n.
103. How many labeled trees are there on 9 nodes?
o 98
o 89
· 97
o 79
o None of these
104. For what n are there exactly 1296 labeled trees?
o n=10
o n=9
o n=8
o n=7
· none of these
105. Consider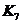 
the complete graph on 7 nodes.
o It has 42 edges and each of its vertices has degree 7
o It has 21 edges and each of its vertices has degree 7
o It has 42 edges and each of its vertices has degree 6
· It has 21 edges and each of its vertices has degree 6
o None of these
106. Consider this adjacency matrix: 
.
o This is the adjacency matrix for a path of length 3.
o This is the adjacency matrix for a cycle of length 4.
o This is the adjacency matrix for a star with 3 arms.
· This is the adjacency matrix for the complete graph on 4 nodes.
o None of these
107. Consider this graph: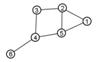 
.
o It is a tree
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|