П | С = принтер | сканер 450. П & М = принтер & монитор 40. C & М = сканер & монитор 50. (П | C) & М = (принтер | сканер) & монитор ?. сканер N1 + N2 + N4 + N5 = 200

П | С = принтер | сканер 450

П & М = принтер & монитор 40

C & М = сканер & монитор 50

(П | C) & М = (принтер | сканер) & монитор?

	С	П	М	П \| С	П & М	C & М	(П \| C) & М
?
?
?
?
?
?


всего

6) проанализируем столбец П | С в этой таблице: его сумма (450) складывается из суммы столбцов С (200) и П (250) – выделены ярким зеленым цветом – плюс последние две строчки (голубой фон), то есть, 450 = 200 + 250 + X, откуда сразу получаем, что X = 0, то есть, последним двум строчкам (запросам) не удовлетворяет ни одного сайта

7) теперь составим таблицы истинности для остальных запросов, отбросив заведомо «нулевые» варианты:

	С	П	М	П \| С	П & М	C & М	(П \| C) & М
?
?
?

?

всего

из оставшихся шести строк таблицы запросы П & М и С & М затрагивают только по одной строчке, поэтому сразу можем вписать соответствующие числа в первый столбец; в последнем запросе, который нас интересует, присутствуют именно эти две строки, то есть, для получения нужно сложить 40 и 50

8) таким образом, правильный ответ: 40 + 50 = 90.

Решение (вариант 3, через диаграммы и систему уравнений):

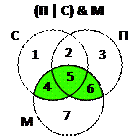
1) для сокращения записи обозначим через C, П, М высказывания «ключевое слово на сайте – сканер» (соответственно принтер, монитор) и нарисуем эти области виде диаграммы (кругов Эйлера); интересующему нас запросу (П | C) & M соответствует объединение областей 4, 5 и 6 («зеленая зона» на рисунке)

2) количество сайтов, удовлетворяющих запросу в области i, будем обозначать через N_i

3) составляем уравнения, которые определяют запросы, заданные в условии:

сканер N1 + N2 + N4 + N5 = 200

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒