
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
NП = 8700, NВ = 7500, NП&В = 3200
N1 + N2 = 8700
N3 + N2 = 7500
N2 = 3200
сразу получаем
N1 + N2 + N3 = 8700 + 7500 - 3200 = 13000
5) таким образом, ответ – 13000.
 Решение (вариант 2, общая формула):
Решение (вариант 2, общая формула):
1) сначала выведем формулу, о которой идет речь; построим диаграмму Эйлера-Венна для двух переменных A и B:
2) обозначим через NA, NB, NA& B и NA|B число страниц, которые выдает поисковый сервер соответственно по запросам A, B, A & B и
A | B
3) понятно, что если области A и B не пересекаются, справедлива формула NA|B=NA+NB
4) если области пересекаются, в сумму NA+NB область пересечения NA& B входит дважды, поэтому в общем случае
NA|B = NA + NB - NA& B
5) в данной задаче
NП = 8700, NВ = 7500, NП& В = 3200
6) тогда находим число сайтов в интересующей нас области по формуле
NП|B = NП + NB – NП& B = 8700 + 7500 – 3200 = 13000
7) таким образом, ответ – 13000.
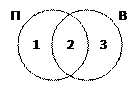 Решение (вариант 3, решение системы уравнений):
Решение (вариант 3, решение системы уравнений):
1) нарисуем области «пирожное» (обозначим ее через П) и «выпечка» (В) в виде диаграммы (кругов Эйлера); при их пересечении образовались три подобласти, обозначенные числами 1, 2 и 3;
2) составляем уравнения, которые определяют запросы, заданные в условии:
пирожное & выпечка N2 = 3200
пирожное N1 + N2 = 8700
выпечка N2 + N3 = 7500
3) подставляя значение N2 из первого уравнения в остальные, получаем
N1 = 8700 - N2 = 8700 – 3200 = 5500
N3 = 7500 - N2 = 7500 – 3200 = 4300
4) количество сайтов по запросу пирожное | выпечка равно
N1 + N2 + N3 = 5500 + 3200 + 4300 = 13000
5) таким образом, ответ – 13000.
Еще пример задания:
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс. ) |
| Динамо & Рубин | |
| Спартак & Рубин | |
| (Динамо | Спартак) & Рубин |
Сколько страниц (в тысячах) будет найдено по запросу
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|