ТЕХНІЧНЕ ЗАВДАННЯ 6 страница

9. 1 Мета заняття

Вивчення методики оцінки міцності та жорсткості конструкції за наявності динамічних вібраційних навантажень.

9. 2 Методичні вказівки з організації самостійної роботи студентів

У процесі експлуатації ЕА елементи несівної конструкції крім статичних навантажень витримують динамічний вплив у вигляді вібрацій. При цьому властивості конструкції ЕА протистояти діям зовнішніх динамічних навантажень також характеризуються механічною міцністю і жорсткістю.

Слід пам’ятати, що з усіх видів механічних впливів вібраційне навантаження є найбільш небезпечним. Його наявність може призвести до втоми матеріалів та руйнування несівних елементів конструкції.

Вібраційне навантаження при розрахунках міцності задається в одній з наступних форм:

- сили, що діє на блок ЕА та змінюється за гармонічним законом:

F = F_m sinω t;

- вібраційного прискорення, що змінюється за законом:

W = W_m sinω t;

- переміщення, що змінюється за законом:

A = A_m sinω t,

де F_m, W_m, A_m – амплітудні значення сили, прискорення та переміщення відповідно;

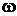– кутова частота вібраційного навантаження.

Готуючись до практичного заняття за даною темою, необхідно вивчити теоретичний матеріал попередніх лекцій і матеріал, викладений в основній [3,
c. 441–445; 4, c. 244–247; 6, c. 220–224] та додатковій [5, c. 235–237] літературі.

9. 2. 1 Визначення міцності та жорсткості конструкції блока ЕА

Очевидно, що між амплітудними значеннями зазначених вище параметрів вібрації існує очевидний зв’язок у вигляді:

W_m = A_m 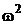та F_m = W_m m,

де m – маса блока, на який діє синусоїдальна вібрація.

Розглянемо випадок кінематичного порушення механічної системи, наприклад, коли вібраційне навантаження, задане вібраційним прискоренням, діє на віброізольований блок ЕА – блок, який встановлено на віброізолятори. Діюче на такий блок вібраційне навантаження (силу) можна подати у вигляді:

F_віб= m W_m 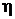_В, (9. 1)

де m – маса конструкції, кг;

W_m – амплітуда вібраційного прискорення, що діє на основу блока ЕА, м/с²;

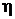_В – коефіцієнт динамічності з урахуванням демпфування системи віброізоляції.

Коефіцієнт динамічності у такому випадку розраховується за формулою:

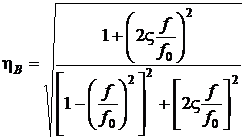, (9. 2)

де f, f₀ – частота зовнішнього вібраційного навантаження та частота власних коливань віброізольованої системи відповідно, Гц;

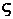– відносне значення коефіцієнта демпфування.

Для віброізольованих систем коефіцієнт демпфування має величину 0, 15…0, 35.

Якщо розглядати вібраційне навантаження як зосереджену силу, що діє, наприклад, на шасі блока ЕА, то розрахунок механічних напруження та деформації виконують за формулами (8. 7), де замість величини P необхідно підставити значення вібраційного навантаження F_віб (9. 1).

Під час виконання практичного заняття за заданим вібраційним навантаженням (механічні впливи у ТЗ) необхідно визначити величини напруження та деформації у блоці ЕА, що проектується, відповідно вищенаведеній методиці.

9. 2. 2 Розрахунок міцності і жорсткості через еквівалентне навантаження

Якщо вважати вібраційне навантаження (силу) рівномірно розподіленим, наприклад, у випадку розгляду вібрацій друкованого модуля, то питоме навантаження його конструкції можна знайти аналогічно формулі (8. 2):

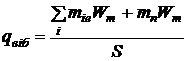де W_m – амплітуда вібраційного прискорення, м/с²,

позначення інших величин такі, як у формулі (8. 2).

Вважаючи це навантаження рівним деякому еквівалентному статичному навантаженню, тобто: 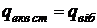, напруження та деформацію плати у залежності від способу закріплення її сторін визначають за формулами (8. 4)–(8. 5) або (8. 6), (8. 7), тобто: 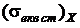, , 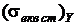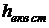. Для визначення діючих значень напружень і прогину конструкції, обумовлених вібраційним прискоренням W_т, необхідно помножити отримані величини на коефіцієнт динамічності 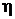_В, розрахований за формулою (9. 2):

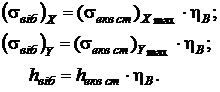(9. 3)

На даному занятті за наявності вібраційного навантаження необхідно визначити величини напруження та деформації друкованого модуля конструкції, який розглядався у попередній роботі, відповідно вищенаведеній методиці.

Отримані значення напружень і деформації необхідно, як і у випадку оцінки статичного навантаження, порівняти з допустимими.

Вібраційні впливи можуть привести до втоми матеріалів конструкції та руйнування її елементів, тому допустимі напруження для різних видів деформацій розраховують за величиною межі витривалості, яка визначається за кривою втоми матеріалу симетричного циклу. Наприклад, у наближених розрахунках для пластичних матеріалів побутових ЕА коефіцієнт запасу міцності при вібраційних навантаженнях дорівнює: 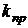= 5…10. Кількісно допустимі напруження розраховуються за формулою (8. 8), а стріла прогину – за (8. 1).

9. 2. 3 Порядок виконання роботи

1. Проаналізувати блок ЕА, який проектується, та визначити який характер має вібраційне навантаження у конструкції.

2. Розрахувати діючі напруження і деформацію несівної блока за вказівками п. 9. 2. 1 та модуля, що розглядався на практичному занятті №8, за формулами (9. 3) за вказівками п. 9. 2. 2.

3. Визначити допустимі напруження та деформацію конструкції. Порівняти розраховані фактичні значення напружень та деформації з допустимими.

4. За результатами проведеного порівняння запропонувати конструктивні заходи для збільшення міцності та жорсткості несівної.

9. 3 Контрольні запитання і завдання

1. Що таке вібровитривалість і вібростійкість ЕА?

2. Що таке вібрації? Якими параметрами вони характеризується?

3. Наведіть модель, яка застосовується під час розгляду вібраційних навантажень несівних конструкцій ЕА.

4. З якою метою у конструкціях ЕА використовуються амортизатори? Якими параметрами вони характеризуються?

5. Які типи амортизаторів ви знаєте? Наведіть міркування щодо їх вибору.

6. У чому особливість розрахунків міцності та жорсткості конструкції ЕА за наявності динамічних вібраційних навантажень?

7. З яких міркувань вибирається величина коефіцієнта запасу міцності?

8. Як визначити коефіцієнт динамічності з урахуванням демпфування механічної системи?

9. У чому різниця розрахунків міцності і жорсткості блока ЕА в залежності від характеру розподілення його маси?

10. Чим обумовлена величина деформації (прогин) пластини за наявності вібраційного навантаження?

9. 4 Приклади аудиторних і домашніх задач

Завдання. Визначити величину циліндричної жорсткості друкованої плати з гетинаксу, товщина якої 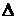= 2 мм.

Розв’язання.

Циліндрична жорсткість пластини визначається за формулою:

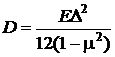де 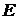– модуль пружності 1-го роду матеріалу пластини, Н/м²;

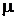– коефіцієнт Пуассона.

Скориставшись даними табл. 7. 2, підставимо відомі величини до формули:

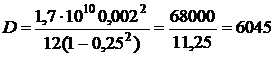(Н).

Відповідь: циліндрична жорсткість пластини дорівнює 6024 Н.

10 ОЦІНКА МІЦНОСТІ ТА ЖОРСТКОСТІ НЕСІВНИХ ЕЛЕМЕНТІВ КОНСТРУКЦІЇ ЕА ПРИ УДАРНИХ НАВАНТАЖЕННЯХ

10. 1 Мета заняття

Вивчення методики оцінки міцності та жорсткості конструкції за наявності ударних навантажень.

10. 2 Методичні вказівки з організації самостійної роботи студентів

У процесі експлуатації ЕА елементи несівної конструкції можуть витримувати удари. Протидією такому впливу є забезпечення необхідної механічної міцності та жорсткості як елементів, так і всієї конструкції.

Ударне навантаження може бути задане у формі імпульсу сили F_уд з амплітудним значенням F_т та тривалістю τ або у формі імпульсу ударного прискорення W з амплітудою W_m та тривалістю τ. Між амплітудними значеннями сили і прискорення є очевидний зв’язок:

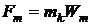, (10. 1)

де m_k – маса конструкції, на який діє удар.

Якщо удар прикладений до шасі, то під m_k, слід розуміти сумарну масу всіх елементів, у тому числі й шасі.

Слід пам’ятати, що форма ударного імпульсу може бути будь-якою – прямокутною, трикутною, синусоїдальною (косинусоїдальною)… У розрахунках ударний імпульс представляють еквівалентним імпульсом прямокутної форми, у якого амплітуда F_т менше максимального значення F_max. Амплітуда еквівалентного імпульсу визначається з умови рівності його площі реальному імпульсу (рис. 10. 1) при однаковій тривалості імпульсу τ. Так, наприклад, амплітуда еквівалентного імпульсу трикутної форми дорівнює F_m. = F_max/2 (рис. 10. 1б), синусоїдального (косинусоїдального) – F_m. = 2F_max/π (рис. 10. 1в).

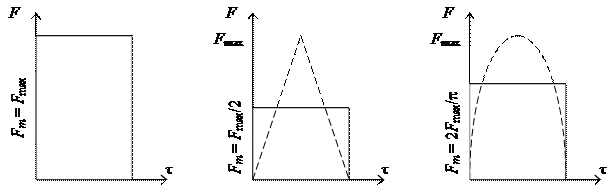
а) б) в)

Рисунок 10. 1

Готуючись до практичного заняття за даною темою, необхідно вивчити теоретичний матеріал попередніх лекцій і матеріал, викладений в основній [3,
c. 441–445; 4, c. 244–247; 6, c. 224–227] та додатковій [5, c. 235–237] літературі.

10. 2. 1 Розрахунокміцності та жорсткості конструкції

Розглянемо випадок кінематичного порушення механічної системи, наприклад, коли ударне навантаження, задане ударним прискоренням, діє на блок ЕА. Розрахунок напружень і деформації при ударі полягає у наступному.

Спочатку розраховують значення напружень і деформації для еквівалентного статичного навантаження, рівного величині ударного імпульсу F_т, за формулами (8. 7). Тобто, для випадку дії зосередженої сили одержують значення , , .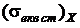

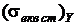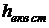Визначають коефіцієнт динамічності при ударному навантаженні. При цьому вважають, що сила удару (10. 1) буде еквівалентна такій, яка має місце при падінні тіла масою m_k з деякої висоти H, тобто:

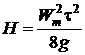де W_m – амплітуда ударного прискорення, м/с²;

τ – тривалість імпульсу, с;

g – прискорення сили тяжіння, м/с².

При зроблених припущеннях коефіцієнт динамічності при ударі виражається таким співвідношенням:

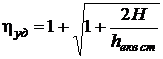, (10. 2)

де 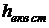– величина еквівалентного статичного прогину при дії ударного навантаження, м.

Далі знаходять значення навантаження при ударі. Для визначення діючих значень напружень і прогину конструкції, обумовлених ударним прискоренням W_т, необхідно помножити отримані їх еквівалентні величини на коефіцієнт динамічності 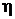_уд, розрахований за формулою (10. 2):

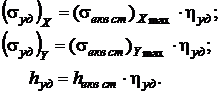(10. 3)

Знайдені значення напружень і деформації при ударі необхідно порівняти з допустимими величинами. Наприклад, у наближених розрахунках для пластичних матеріалів побутових ЕА коефіцієнт запасу міцності при ударах дорівнює: 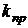= 2…5. Кількісно допустимі напруження розраховуються за формулою (8. 8), а стріла прогину – за (8. 1).

10. 2. 2 Порядок виконання роботи

1. Проаналізувати блок ЕА, який проектується, та визначити величину ударного впливу на конструкцію за вимогами ТЗ.

2. Розрахувати діючі напруження і деформацію модуля, що розглядався на попередніх практичних заняттях №8, 9, та всього блока за вказівками п. 10. 2. 1 і формулами (10. 3).

3. Визначити допустимі напруження та деформацію конструкції. Порівняти розраховані фактичні значення напружень і деформації з допустимими.

10. 3 Контрольні запитання і завдання

1. Що таке удари? Якими параметрами характеризуються удари?

2. Що таке ударостійкість конструкції ЕА? Чим вона обумовлена?

3. Наведіть модель, яка застосовується під час розгляду ударних навантажень несівних конструкцій ЕА.

4. Чим обумовлена величина деформації (прогин) пластини за наявності ударного навантаження?

5. У чому особливість розрахунків міцності та жорсткості конструкції ЕА за наявності ударних навантажень?

6. Як впливає форма імпульсу сили на величину ударного навантаження?

7. Наведіть конструктивні заходи збільшення міцності та жорсткості різних несівних конструкцій при ударах.

8. Наведіть міркування щодо доцільності застосування амортизаторів як засобу захисту від ударів.

9. Як визначити коефіцієнт динамічності при ударі? Від чого залежить його величина?

10. Наведіть послідовність розрахунку сумарної деформації (прогину) конструкції при дії статичних і динамічних навантажень.

10. 4 Приклади аудиторних і домашніх задач

Завдання. Визначити амплітуди еквівалентного ударного імпульсу для синусоїдального та трикутного імпульсів сили амплітудою 15 кг× м/с².

Розв’язання.

У розрахунках ударний імпульс будь-якої форми представляють еквівалентним імпульсом прямокутної форми. За умови рівності площин імпульсів для випадку синусоїдальної форми маємо:

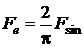де 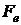– амплітуда імпульсу прямокутної форми, кг× м/с²;

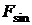– амплітуда синусоїдального імпульсу, кг× м/с².

Підставляємо відомі дані:

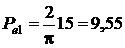(кг× м/с²).

Тобто, амплітуда еквівалентного ударного імпульсу значно менша за амплітуду діючого синусоїдального імпульсу.

Для випадку трикутної форми імпульсу маємо:

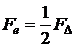де 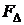– амплітуда трикутного імпульсу, кг× м/с².

Підставляємо відомі дані:

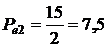(кг× м/с²).

Тобто, амплітуда еквівалентного ударного імпульсу вдвічі менша за амплітуду діючого трикутного імпульсу.

Відповідь: амплітуда еквівалентного ударного імпульсу для синусоїдального імпульсу сили дорівнює 9, 55 кг× м/с², для трикутного імпульсу – 7, 5 кг× м/с².

11 РОЗРАХУНОК ПАРАМЕТРІВ ГВИНТОВИХ З’ЄДНАНЬ

11. 1 Мета заняття

Вивчення методики розрахунку параметрів гвинтових з’єднань у конструкції.

11. 2 Методичні вказівки з організації самостійної роботи студентів

Одним з найпоширеніших способів механічного з’єднання електричних вузлів та елементів несівної конструкції у блоці ЕА є з’єднання за допомогою гвинтів. Гвинти мають стандартні типи та ряд різьб. На рис. 11. 1 наведено два стандартних типи гвинтів і варіанти вимірювання їх параметрів.

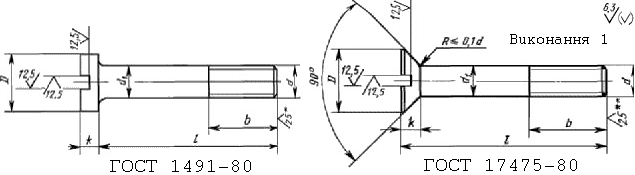
Рисунок 11. 1

Слід пам’ятати, що необхідна кількість гвинтів у блоці та їх параметри залежать від особливості конструкції ЕА і величини навантажень, які виникають у процесі його експлуатації.

Готуючись до практичного заняття за даною темою, необхідно вивчити теоретичний матеріал попередніх лекцій і матеріал, викладений в основній [6, c. 280–283] та додатковій [7, c. 230–232] літературі.

11. 2. 1 Розрахунок параметрів гвинтових з’єднань

Гвинтові з’єднання, за допомогою яких кріплять окремі вузли до несівної або виконують з’єднання її елементів, можуть витримувати деформації розтягування, зсуву, згину. Наприклад, елементи кріплення панелей конструкції до корпусу ЕА розраховують на міцність за умови, що виникаючі напруження зсуву s не перевищують допустимі [s], тобто:

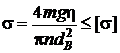, (11. 1)

де т – маса блока, до якого закріплюється панель, кг;

g – прискорення сили тяжіння, м/с²;

h - коефіцієнт динамічності;

n – кількість гвинтів;

d_B – внутрішній діаметр гвинта, м.

Для такого розрахунку коефіцієнт динамічності вибирають максимальним з його значень при динамічному навантаженні (при вібраціях або ударах).

Слід враховувати, що якщо статичні і динамічні навантаження діють спільно на конструкцію, то має місце принцип суперпозиції. За таким принципом результуюча деформація дорівнює сумі деформацій, обумовлених дією статичних і динамічних навантажень:

h_S = h_cm + h_віб + h_уд,

де h_ст, h_віб, h_уд – деформація (прогин) за рахунок статичного, вібраційного та ударного навантаження, відповідно.

Аналогічно результуюче максимальне напруження є результатом суперпозиції напружень, обумовлених кожним навантаженням:

s_max = (s_max)_ст + (s_max)_віб + (s_max)_уд, (11. 2)

де (s_max)_ст, (s_max)_віб, (s_max)_уд – напруження у конструкції за рахунок статичного, вібраційного та ударного навантаження відповідно.

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒