
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ТЕХНІЧНЕ ЗАВДАННЯ 3 страница
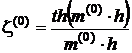 ,
,
де 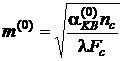 (
( 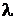 – теплопровідність матеріалу ребра).
– теплопровідність матеріалу ребра).
3. Визначають початкове значення сумарного коефіцієнта теплообміну з урахуванням конвективної, променевої та кондуктивної складової:
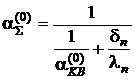 .
.
4. Розраховують початкову температуру поверхні радіатора згідно з (4. 3):
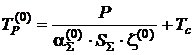
та середню температуру повітря біля елемента:
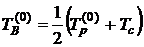 .
.
Подальші ітерації виконують з метою послідовного поліпшення всіх значень величин  ,
,  ,
, 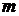 ,
, 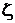 ,
, 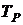 ,
, 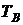 .
.
5. Обчислюють деякі характерні числа, прийняті в аеродинаміці, що визначають протікання конвективного потоку, який охолоджує радіатор з установленим елементом. До них відносяться числа Грасгоффа 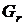 та Нуссельта
та Нуссельта 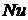 .
.
Перше число характеризує протікання конвективного потоку з урахуванням температури і в’язкості повітря, друге – з урахуванням теплообміну між тілом, що охолоджується, і потоком.
Визначають початкове наближення числа Грасгоффа:
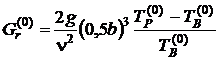 ,
,
де 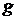 – прискорення сили тяжіння, м/с2;
– прискорення сили тяжіння, м/с2;
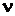 – коефіцієнт кінематичної в’язкості, який приймає значення в залежності від температури повітря (табл. 4. 3).
– коефіцієнт кінематичної в’язкості, який приймає значення в залежності від температури повітря (табл. 4. 3).
Таблиця 4. 3 – Значення коефіцієнта кінематичної в’язкості
| Т, оC | ||||||
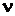 , м2/с , м2/с
| 1, 33× 10-5 | 1, 56× 10-5 | 1, 7× 10-5 | 1, 89× 10-5 | 2, 11× 10-5 | 2, 31× 10-5 |
За отриманим значенням 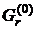 знаходять критеріальний коефіцієнт:
знаходять критеріальний коефіцієнт:
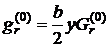 .
.
Число Нуссельта розраховують у залежності від значення 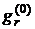 :
:
- якщо 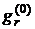 < 7, то початкове значення числа Нуссельта визначають, як
< 7, то початкове значення числа Нуссельта визначають, як
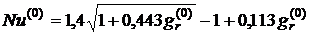 ;
;
- якщо 7 ≤ 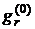 ≤ 20, то
≤ 20, то
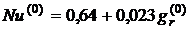 ;
;
- якщо 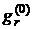 > 20, то
> 20, то
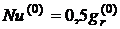 .
.
6. За значенням числа Нуссельта розраховують конвективний коефіцієнт теплообміну у першому наближенні:
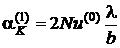 ,
,
де 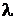 =2, 8 10-2 – коефіцієнт теплопровідності повітря.
=2, 8 10-2 – коефіцієнт теплопровідності повітря.
7. Знаходять променевий коефіцієнт теплообміну у першому наближенні:
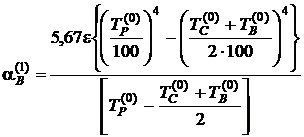 .
.
8. Визначають сумарний коефіцієнт теплообміну у першому наближенні з урахуванням конвективної та променевої складової:
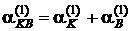
та сумарний коефіцієнт теплообміну з урахуванням кондуктивної складової:
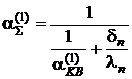 .
.
9. Визначають у першому наближенні коефіцієнт 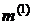 :
:
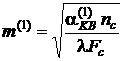
та коефіцієнт ефективності ребра:
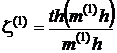 .
.
10. Визначають у першому наближенні температуру радіатора 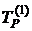 :
:
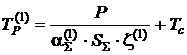 .
.
11. Продовжують ітеративний процес обчислення коефіцієнтів 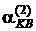 ,
, 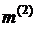 ,
, 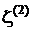 ,
, 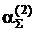 ,
, 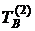 та
та 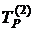 і так далі. Ознакою завершення процесу послідовних наближень є виконання співвідношення:
і так далі. Ознакою завершення процесу послідовних наближень є виконання співвідношення:
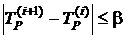 ,
,
де 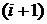 ,
, 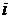 – номери послідовних наближень;
– номери послідовних наближень;
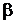 – довільно вибране число (наприклад, 3 оС).
– довільно вибране число (наприклад, 3 оС).
Тепловий режим задовільний, якщо виконується співвідношення (4. 2).
4. 2. 4 Порядок виконання роботи
1. За результатами проведеного у лабораторній роботі №1 аналізу схеми електричної принципової ЕА вибрати один-два найбільш теплонавантажених елементів для встановлення їх на радіатор.
2. Для вибраних елементів визначити габаритні розміри та потужність, яку вони розсіюють.
3. Спроектувати конструкцію радіатора за вказівками п. 4. 2. 2 та визначити його ефективність за співвідношенням (4. 1).
4. Розрахувати тепловий режим елементів, встановлених на радіаторі, за розглянутою у п. 4. 2. 3 методикою.
4. 3 Контрольні запитання і завдання
1. Який фізичний механізм використовують для охолодження теплонавантаженого елемента при його встановленні на радіатор?
2. Опишіть конструкцію штирьового радіатора.
3. Як конструктивно виконується кріплення теплонавантаженого модуля на радіаторі для охолодження?
4. Які фізичні процеси охолодження характеризують числа Нуссельта та Грасгоффа при обтіканні тіла, що охолоджується, повітряним потоком?
5. У чому суть методу послідовних наближень при розв’язанні рівняння теплового балансу?
6. Що є критерієм правильності вибору конструкції пластинчастого радіатора?
7. Якими конструктивними параметрами визначається ефективна висота ребра радіатора?
8. Як впливає ширина каналу між ребрами пластинчастого радіатора на ефективність охолодження?
9. Які конструктивні заходи підвищення ефективності охолодження за допомогою радіаторів ви знаєте?
10. Наведіть основні конструктивні заходи щодо забезпечення нормального температурного режиму роботи блока ЕА.
4. 4 Приклади аудиторних і домашніх задач
Завдання. Визначити площу тепловіддачі мікросхеми К174 ХА17.
Розв’язання.
Мікросхема К174 ХА17 призначена для роботи у пристроях побутової та багатофункціональної аналогової апаратури і є аналогом TDA 3501.
Конструктивно мікросхема виконана у DIP-корпусі з габаритними розмірами – 36х15 мм. Товщина тіла мікросхеми 3 мм, кількість виводів – 28.
Якщо прийняти нагріту зону – тіло мікросхеми – у вигляді паралелепіпеда, то поверхня тепловіддачі визначається як:
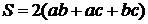 , [м2]
, [м2]
де a, b, c – габаритні розміри нагрітої зони, м.
Підставимо у формулу габарити тіла мікросхеми. Маємо:
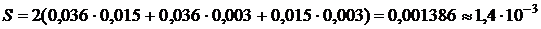 (м2).
(м2).
Відповідь: площа тепловіддачі мікросхеми дорівнює 1, 4× 10-3 м2.
5 РОЗРАХУНОК ЕЛЕКТРИЧНОЇ МІЦНОСТІ ВИСОКОВОЛЬТНОГО
БЛОКА ЕА
5. 1 Мета заняття
Аналіз компонувальної схеми високовольтного блока ЕА та вивчення методики розрахунку його електричної міцності.
5. 2 Методичні вказівки з організації самостійної роботи студентів
Важливо пам’ятати, що електричне поле у високовольтному блоці ЕА є неоднорідним. Під впливом природних іонізаторів (ультрафіолетового випромінювання, космічної радіації) в одиничному об’ємі повітря завжди є деяка кількість іонізованих частинок – електронів та іонів. Електрони, як частинки, що мають малу масу, прискорюються електричним полем і здобувають значної швидкості. Зіштовхнувшись з нейтральним атомом повітря, вони викликають утворення нової пари електрон-іон. За певних умов цей процес набуває лавиноподібного характеру, що веде до утворення провідного " містка" у повітряному проміжку між парою різнополярних високовольтних виводів. Так відбувається пробій ізоляційного проміжку, обумовлений ударною іонізацією.
Напруга між двома високовольтними виводами, при якому може виникнути пробій (пробивна напруга), залежить від ряду факторів: тиску повітря всередині блока ЕА, температури, вологості, концентрації пилу, відстані між виводами, а також від геометричних розмірів і форми виводів. Чим менше еквівалентний радіус виводу (чим він " гостріше" ), тим більш неоднорідне електричне поле і тим вища ймовірність пробою повітряного проміжку між виводами.
При оцінці впливу геометричної форми виводів на стан електричного поля між ними використовують такі моделі для розрахунку пробивної напруги:
- " площина–площина" (поле практично однорідне);
- " стержень–площина" (поле між виводами неоднорідне);
- " стержень–стержень" (поле між виводами дуже неоднорідне).
Величина розрядної напруги залежить також і від виду напруги: постійна, змінна, імпульсна; позитивної або негативної полярності.
При розрахунках розрядної напруги кліматичні фактори враховуються за приведеним значенням відносної щільності повітря у блоці ЕА:
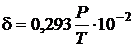 , (5. 1)
, (5. 1)
де 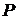 – тиск усередині блока, Па;
– тиск усередині блока, Па;
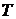 – температура у блоці, K.
– температура у блоці, K.
На практичному занятті величини Р і Т вибираються за вимогами ТЗ.
Електрична міцність ЕА для випадку, коли ізоляційним проміжком між високовольтними різнополярними виводами є повітря, вище, ніж при заповненні цього проміжку ізоляційним матеріалом. У такому випадку розрахунок пробивної напруги проводиться за різними розрахунковими формулами.
Готуючись до практичного заняття за даною темою, необхідно вивчити
теоретичний матеріал попередніх лекцій і матеріал, викладений в основній [3,
с. 420–430; 4, с. 109–112] та додатковій [5, с. 318–319] літературі.
5. 2. 1 Розрахунок пробивної напруги через повітряний ізоляційний проміжок
Оцінка електричної міцності блока ЕА в залежності від його конструкції проводиться за різними формулами. В табл. 5. 1 наведені співвідношення для розрахунку пробивної напруги 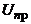 між високовольтними різнополярними виводами. Конструктивні вирішення враховуються такими коефіцієнтами:
між високовольтними різнополярними виводами. Конструктивні вирішення враховуються такими коефіцієнтами:
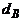 – довжина повітряного ізоляційного проміжку, м;
– довжина повітряного ізоляційного проміжку, м;
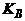 – коефіцієнт, який враховує вплив відносної вологості повітря на електричну міцність блока (табл. 5. 2);
– коефіцієнт, який враховує вплив відносної вологості повітря на електричну міцність блока (табл. 5. 2);
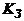 – коефіцієнт, який враховує вплив запилення повітря на електричну міцність (табл. 5. 3);
– коефіцієнт, який враховує вплив запилення повітря на електричну міцність (табл. 5. 3);
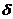 – відносна щільність повітря (формула (5. 1)), Па/К.
– відносна щільність повітря (формула (5. 1)), Па/К.
Таблиця 5. 1 – Співвідношення для розрахунку пробивної напруги
через повітряний ізоляційний проміжок
| № | Модель розрядного проміжку | Вид напруги | Формула для розрахунку пробивної напруги 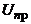 , кВ , кВ
|
| Стержень – площина | Постійна напруга позитивної полярності | 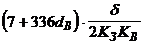
| |
| Стержень – площина | Позитивна імпульсна напруга | 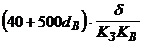
| |
| Стержень – площина | Негативна імпульсна напруга | 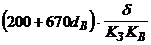
| |
| Стержень – площина | Змінна напруга частотою 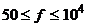 Гц Гц
| 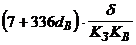
| |
| Стержень – площина | Змінна напруга частотою 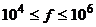 Гц Гц
| 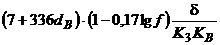
| |
| Стержень – площина | Змінна напруга частотою 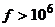 Гц Гц
| 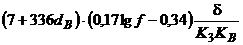
| |
| Стержень – стержень | Постійна напруга позитивної полярності | 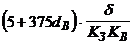
| |
| Стержень – стержень | Постійна напруга негативної полярності | 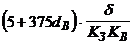
| |
| Стержень – стержень | Позитивна імпульсна напруга | 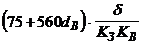
| |
| Стержень – стержень | Негативна імпульсна напруга | 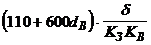
|
Продовження табл. 5. 1
| Стержень – стержень | Змінна напруга частотою 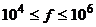 Гц Гц
| 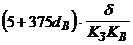
| |
| Стержень – стержень | Змінна напруга частотою 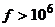 Гц Гц
| 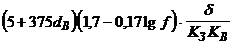
|
Таблиця 5. 2 – Значення коефіцієнта 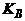
| Відносна вологість, % | ||||||
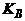
| 1, 05 | 1, 08 | 1, 1 | 1, 12 | 1, 15 |
Таблиця 5. 3 – Значення коефіцієнта 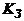
| Запилення повітря, мг/м3 | ||||||||||
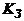
| 1, 0 | 1, 05 | 1, 12 | 1, 125 | 1, 128 | 1, 13 | 1, 15 | 1, 18 | 1, 2 | 1, 212 |
5. 2. 2 Розрахунок пробивної напруги через поверхню ізолятора
При розрахунку пробивної напруги через поверхню ізолятора 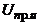 слід користуватися такою формулою:
слід користуватися такою формулою:
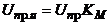 , (5. 2)
, (5. 2)
де 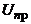 – значення пробивної напруги, розрахованої за формулами табл. 5. 1, в яких замість величини
– значення пробивної напруги, розрахованої за формулами табл. 5. 1, в яких замість величини 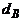 необхідно підставити довжину розрядного проміжку на поверхні ізолятора
необхідно підставити довжину розрядного проміжку на поверхні ізолятора 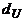 , а замість величин
, а замість величин 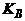 і
і 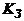 – відповідні значення коефіцієнтів
– відповідні значення коефіцієнтів 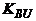 (табл. 5. 4) і
(табл. 5. 4) і 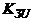 (табл. 5. 5);
(табл. 5. 5);
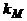 – коефіцієнт, який характеризує вплив матеріалу ізолятора на електричну міцність блока (табл. 5. 6).
– коефіцієнт, який характеризує вплив матеріалу ізолятора на електричну міцність блока (табл. 5. 6).
Таблиця 5. 4 – Значення коефіцієнта 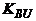
| Відносна вологість, % | ||||||
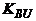
| 1, 20 | 1, 40 | 1, 60 | 1, 85 | 2, 50 | 2, 85 |
Таблиця 5. 5 – Значення коефіцієнта 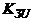
| Запилення ізолятора, мг/м3 | |||||||||
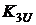
| 1, 125 | 1, 128 | 1, 130 | 1, 138 | 1, 140 | 1, 160 | 1, 170 | 1, 210 | 1, 350 |
Таблиця 5. 6 – Значення коефіцієнта 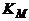
| Матеріал ізолятора | Кераміка | Фарфор | Текстоліт | Фторопласт |
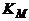
| 0, 9 | 0, 85 | 0, 75 | 0, 70 |
5. 2. 3 Оцінка електричної міцності блока ЕА
Характеристикою електричної міцності блока ЕА є порівняння величин пробивної напруги 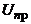 та
та 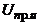 зі значенням робочої напруги
зі значенням робочої напруги 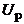 . Таке порівняння роблять за величиною коефіцієнта запасу електричної міцності
. Таке порівняння роблять за величиною коефіцієнта запасу електричної міцності 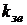 , рівного відношенню пробивної напруги та робочої:
, рівного відношенню пробивної напруги та робочої:
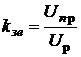 . (5. 3)
. (5. 3)
Розраховані значення 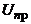 та
та 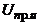 треба розглядати як середні для заданих умов експлуатації, які мають нормальний закон розподілу. Середньоквадратичне їх відхилення лежить в межах 0. 5…5%
треба розглядати як середні для заданих умов експлуатації, які мають нормальний закон розподілу. Середньоквадратичне їх відхилення лежить в межах 0. 5…5% 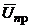 (де
(де 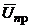 – середнє значення пробивної напруги). Ймовірною характеристикою електричної міцності є ймовірність відсутності пробою:
– середнє значення пробивної напруги). Ймовірною характеристикою електричної міцності є ймовірність відсутності пробою:
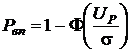 ,
,
де 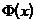 – інтеграл ймовірності.
– інтеграл ймовірності.
При значеннях 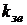 ≥ 1. 5…2 та імовірності відсутності пробою
≥ 1. 5…2 та імовірності відсутності пробою 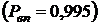 електрична міцність ЕА може вважатися задовільною.
електрична міцність ЕА може вважатися задовільною.
На рис. 5. 1 наведено приклад фрагмента конструкції високовольтного блока живлення – фільтрового конденсатора, до виводів якого підведена випрямлена напруга 27 кВ позитивної полярності. Стрілками показані можливі напрямки пробою – між високовольтним виводом і найближчою стінкою корпуса блока через повітряний зазор між ними (а), по поверхні ізолятора на корпус (б).
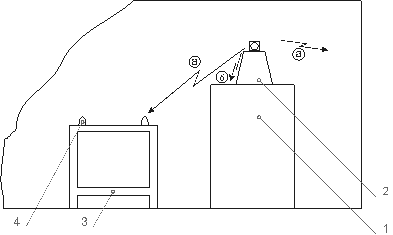
1 – високовольтний конденсатор фільтра; 3 – дросель фільтра;
2 – високовольтний вивід конденсатора; 4 – виводи дроселя.
Рисунок 5. 1
5. 2. 3 Порядок виконання роботи
1. Проаналізувати конструкцію, що проектується, на наявність високовольтних елементів. Вивчити місця можливого електричного пробою через повітряний проміжок та на ізоляторі і підготувати дані для розрахунку електричної міцності блока ЕА за вимогами ТЗ.
За відсутності необхідності оцінки електричної міцності конструкції, що проектується, отримати у керівника заняття варіант компонування високовольтного блока та скористатися даними табл. 5. 7.
Таблиця 5. 7 – Варіанти для розрахунку
| Варіант | ||||||||||||
| Номер моделі | ||||||||||||
| Довжина проміжку, мм | 2, 5 | 3, 0 | 5, 0 | 0, 7 | ||||||||
| Температура, оС | ||||||||||||
| Атмосферний тиск, кПа | ||||||||||||
| Відносна вологість, % | ||||||||||||
| Запилення повітря, мг/м3 | ||||||||||||
| Матеріал ізолятора | Кераміка | Фарфор | Текстоліт | Фторопласт | Кераміка | Фарфор | Текстоліт | Фторопласт | Кераміка | Фарфор | Текстоліт | Фторопласт |
| Запилення ізолятора, мг/м3 | ||||||||||||
2. Розрахувати величину пробивної напруги через повітряний ізоляційний проміжок за вказівками п. 5. 2. 1.
3. Розрахувати величину пробивної напруги на поверхні ізолятора за вказівками п. 5. 2. 2.
4. Розрахувати значення коефіцієнта запасу електричної міцності за співвідношенням (5. 3) та зробити за отриманими результатами висновки.
5. 3 Контрольні запитання і завдання
1. Як впливають кліматичні фактори (тиск повітря та температура всередині блока) на електричну міцність ЕА?
2. Чому запилення повітря разом з вологістю знижує електричну міцність?
3. Що таке діелектричні бар’єри та як їх використовують у конструкціях високовольтних блоків ЕА для підвищення електричної міцності?
4. У чому фізичний сенс розгляду моделі повітряного проміжку і форми виводів елементів при розрахунку пробивної напруги?
5. Наведіть конструктивні заходи з підвищення електричної міцності ЕА.
6. Чому повітряний проміжок між високовольтними виводами більш міцний, ніж у випадку його заповнення фарфоровим ізолятором?
7. Які чисельні величини характеризують електричну міцність ЕА?
8. Як можна визначити мінімальну величину ізоляційного проміжку за значенням коефіцієнта запасу електричної міцності?
9. Наведіть номенклатуру матеріалів, які використовуються для виготовлення ізоляторів для високовольтних блоків ЕА.
10. Як впливає вид напруги на електричну міцність ЕА?
5. 4 Приклади аудиторних і домашніх задач
Завдання. Визначити величину пробивної напруги частотою 1 кГц високовольтного конденсатора фільтра (рис. 5. 1) через керамічний ізолятор
( 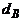 = 5 мм), якщо запилення ізолятора 10 мг/м3. Умови експлуатації блока фільтра відповідають УХЛ 4. 1 за ГОСТ 15150-69.
= 5 мм), якщо запилення ізолятора 10 мг/м3. Умови експлуатації блока фільтра відповідають УХЛ 4. 1 за ГОСТ 15150-69.
Розв’язання.
Відповідно до умов експлуатації гіршими (з позиції електричної міцності) будуть такі умови: температура навколишнього середовища – Т = +40 0С, вологість – 80%, атмосферний тиск – Р = 100 кПа.
Відносна щільність повітря у блоці фільтра:
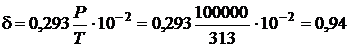 (Па/К).
(Па/К).
Для розрахунку електричної міцності блока скористаємось моделлю за варіантом 4 (табл. 5. 1). Розрахуємо величину пробивної напруги за формулою:
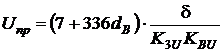 ,
,
де 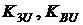 – коефіцієнти, що визначаються за даними табл. 5. 4, 5. 5.
– коефіцієнти, що визначаються за даними табл. 5. 4, 5. 5.
Величина пробивної напруги по поверхні ізолятора визначається як
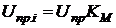 ,
,
де 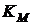 – коефіцієнт, що знаходиться за даними табл. 5. 6.
– коефіцієнт, що знаходиться за даними табл. 5. 6.
Тобто, кінцева розрахункова формула має вигляд:
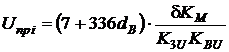 .
.
Підставимо необхідні дані до вищенаведеної формули. Маємо:
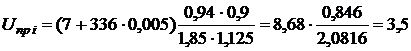 (кВ).
(кВ).
Відповідь: величина пробивної напруги через керамічний ізолятор дорівнює 3, 5 кВ.
6 РОЗРОБКА КОНСТРУКЦІЇ ЕЛЕКТРОМАГНІТНОГО ЕКРАНА ТА
ОЦІНКА ЙОГО ЕФЕКТИВНОСТІ
6. 1 Мета заняття
Вивчення методики проектування електромагнітного екрана та оцінки його ефективності.
6. 2 Методичні вказівки з організації самостійної роботи студентів
Електромагнітне екранування є одним з конструктивних заходів забезпечення електромагнітної сумісності елементів і модулів у блоці ЕА. Екранують, як правило, або імовірні приймачі завад (ПЗ), або імовірні джерела завад (ДЗ).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|