ТЕХНІЧНЕ ЗАВДАННЯ 5 страница

Циліндрична жорсткість пластини визначається за формулою:

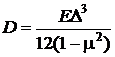, (7. 4)

де 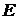– модуль пружності 1-го роду матеріалу пластини, Н/м²;

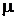– коефіцієнт Пуассона (табл. 7. 2).

За формулою (7. 3) розраховують, наприклад, частоту коливань друкованих модулів, які закріплено у конструкції гвинтами по чотирьох кутах.

3. При оцінюванні дії на конструкцію зовнішніх механічних впливів використовується коефіцієнт динамічності, який показує, у скільки разів збільшиться деформація (прогин) пластини при дії синусоїдального вібраційного навантаження з частотою 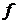, порівняно з деформацією, обумовленою статичним навантаженням (за рахунок сили тяжіння). При наближених розрахунках у нерезонансній області коефіцієнт динамічності визначається за формулою:

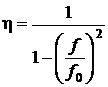. (7. 5)

де 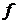– частота зовнішнього механічного впливу, Гц;

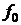– власна частота механічних коливань, Гц.

Формулу (7. 5) розраховують для деяких значень зовнішніх частот, наприклад, граничних і середнього значення частот механічних впливів при експлуатації ЕА. Але така формула має дуже приблизний характер. Вона не враховує реального демпфування в конструкції, обумовлене варіантом закріплення.

7. 2. 2 Порядок виконання роботи

1. Проаналізувати ЕА, що проектується, та визначитися за результатами лабораторної роботи №3 з масогабаритними параметрами і складом друкованих модулів конструкції.

2. За вибором викладача розрахувати частоту власних коливань одного з модулів конструкції, використовуючи, в залежності від варіанта його кріплення, співвідношення (7. 2) або (7. 3).

2. За формулою (7. 5) розрахувати коефіцієнт динамічності для граничних і середнього значення частот механічних впливів при експлуатації ЕА, що обумовлюється вимогами ТЗ (група за ГОСТ 16019-2001 або ГОСТ 25467-82).

3. З’ясувати, чи має місце резонанс для заданих умов експлуатації. Запропонувати конструктивні заходи для збільшення демпфування конструкції.

7. 3 Контрольні запитання і завдання

1. Дайте визначення механічної жорсткості та міцності конструкції ЕА. Якими фізичними величинами вони характеризуються?

2. Які параметри модуля з навісним монтажем впливають на його власну частоту коливань?

3. Як впливає жорсткість закріплення сторін пластини на величину частоти її власних коливань?

4. Як впливає маса розміщених на модулі елементів на частоту його власних коливань?

5. Які параметри матеріалу пластини впливають на величину частоти її власних коливань?

6. Як при заданій площі модуля можливо змінити частоту його власних коливань у потрібний бік?

7. Опишіть і виконайте ескізне креслення основного та двох видів коливань вищих типів для таких випадків:

- жорсткого закріплення двох протилежних сторін модуля при двох інших вільних;

- при закріпленні пластини у чотирьох кутах.

8. На які параметри ЕА найбільш суттєво впливає наявність механічного резонанса?

9. Наведіть залежність коефіцієнта динамічності від частоти.

10. Запропонуйте конструктивні заходи збільшення демпфування модуля.

7. 4 Приклади аудиторних і домашніх задач

Завдання. Визначити коефіцієнт динамічності блока ЕА, власна частота коливань якого 10 Гц, на частоті 1 Гц.

Розв’язання.

У нерезонансній області коефіцієнт динамічності блока ЕА приблизно можливо визначити за формулою:

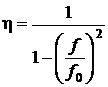Підставимо відомі величини до формули. Маємо:

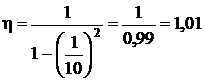Відповідь: коефіцієнт динамічності блока ЕА дорівнює 1, 01.

8 ОЦІНКА МІЦНОСТІ ТА ЖОРСТКОСТІ НЕСІВНИХ ЕЛЕМЕНТІВ КОНСТРУКЦІЇ ЕА ПРИ СТАТИЧНИХ НАВАНТАЖЕННЯХ

8. 1 Мета заняття

Вивчення методики оцінки міцності та жорсткості конструкції за наявності статичних навантажень.

8. 2 Методичні вказівки з організації самостійної роботи студентів

У процесі експлуатації ЕА будь-яка несівна під дією сили тяжіння на окремі елементи конструкції витримує статичні навантаження. Властивості конструкції протистояти діям зовнішніх механічних навантажень характеризуються механічною міцністю та жорсткістю.

Міцність – це характеристика конструкції відносно виникаючих у ній напружень (нормальних – 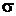та тангенціальних – 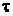). Конструкція вважається міцною, якщо напруження не перевищують деякої допустимої величини, тобто:

; ,

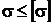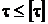де 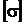, 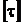– допустимі значення напруження (перша теорія міцності).

У свою чергу, конструкція вважається жорсткою, якщо величина її деформації не перевищує допустимої величини:

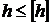де 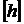– допустиме значення деформації.

Тут і далі розглядатимемо лише лінійні деформації.

Наступні три теми практичних занять присвячені оцінці міцності та жорсткості елементів несучої конструкції, які можливо звести до моделі пластини, тобто конструкції, у якій два розміри набагато більші третього. За такою моделлю можна розраховувати: плати, шасі, друковані модулі, панелі з встановленими на них елементами тощо. В залежності від величини деформації (прогину) пластини, під дією ваги встановлених на них елементів або впливу зовнішніх динамічних навантажень, вони розрізняються на:

- жорсткі пластини – пластини, в яких найбільший прогин (стріла прогину) 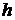не перевершує чверті її товщини 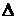, тобто: 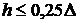; (8. 1)

- гнучкі пластини, для яких – ;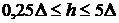

- мембрани, для яких – .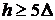

Для несiвних конструкцій блоків ЕА застосовується модель першого типу, для якої справедливе співвідношення (8. 1). Інші типи моделей використовуються під час розгляду деяких спеціальних модулів з друкованим монтажем.

При такому аналізі, як правило, припускається, що зовнішні сили діють перпендикулярно площині пластини (рис. 7. 1), а навантаження розподілене практично рівномірно по її поверхні. Статичне навантаження у такій системі обумовлюється безпосередньою дією сил тяжіння та відповідною реакцією опор, а значення напруження та деформацій залежать від типу закріплення.

Готуючись до практичного заняття за даною темою, необхідно вивчити теоретичний матеріал попередніх лекцій і матеріал, викладений в основній [3,
c. 441–445; 4, c. 244–247] та додатковій [5, c. 235–237] літературі.

8. 2. 1 Розв’язання задачі аналізу

Величина питомого статичного навантаження для друкованого модуля або панелі зі встановленими на ній елементами визначається як

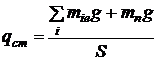, (8. 2)

де 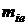, 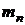– маса і-го елемента або вузла, розміщених на платі (шасі), та маса плати, відповідно, кг;

g – прискорення сили тяжіння, м/с²;

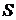– площа поверхні плати, м².

Зверніть увагу, що розрахункові формули значень напруження та деформацій при відомих параметрах конструкції залежить від типу закріплення пластини. Розглянемо найбільш поширені випадки.

1. Випадок жорсткого закріплення всіх сторін пластини, що характерно для малогабаритних автономних блоків ЕА (рис. 7. 2, варіант 6), або коли всі сторони пластини вільно оперті (рис. 7. 2, варіант 3).

Згинаючий момент навколо осі 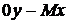, який припадає на одиницю довжини сторони 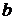, та згинаючий момент відносно осі 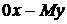, який припадає на одиницю довжини сторони 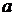, є:

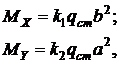, (8. 3)

де 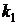, 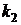– коефіцієнти, які визначаються за даними табл. 8. 1.

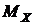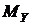За максимальним значенням і визначають максимальне нормальне напруження у перетині, перпендикулярному осі 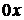, та максимальне нормальне напруження у перетині, перпендикулярному осі 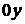, на початку координат:

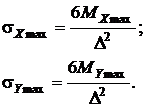(8. 4)

Тангенціальні напруження, які діють у цих перетинах, за величинами значно менші, і їх можна не розраховувати.

Максимальна деформація – стріла прогину пластини – розраховується за формулою:

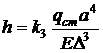, (8. 5)

де 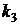– коефіцієнт, який залежить від відношення сторін пластини та типу закріплення (табл. 8. 1);

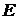– модуль пружності 1-го роду матеріалу пластини, Н/м².

Таблиця 8. 1 – Значення коефіцієнтів 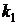, , 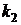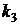для випадків жорсткого та вільно обпертого закріплення чотирьох сторін пластини

	Всі сторони жорстко закріплені			Всі сторони вільно обперті

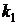
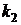
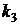
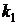
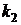
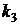
1, 0	0, 022	0, 022	0, 014	0, 046	0, 046	0, 046
1, 1	0, 025	0, 022	0, 017	0, 053	0, 047	0, 054
1, 2	0, 020	0, 022	0, 020	0, 061	0, 048	0, 063
1, 3	0, 032	0, 021	0, 021	0, 068	0, 047	0, 072
1, 4	0, 034	0, 019	0, 023	0, 074	0, 047	0, 079
1, 5	0, 036	0, 018	0, 025	0, 080	0, 046	0, 087
1, 6				0, 085	0, 045	0, 093
1, 7			0, 026	0, 089	0, 044	0, 099
1, 8				0, 094	0, 043	0, 105
1, 9			0, 027	0, 097	0, 042	0, 109
2, 0				0, 101	0, 041	0, 114
3, 0	0, 037	0, 019	0, 028	0, 119	0, 034	0, 138
4, 0				0, 123	0, 032	0, 144
5, 0			0, 029	0, 124	0, 031	0, 146
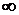
	0, 038	0, 020	0, 030	0, 125	0, 031	0, 146

2. Випадок жорсткого закріплення двох довгих (рис. 7. 2, варіант 5) або двох коротких (рис. 7. 2, варіант 4) сторін при вільно опертих інших, що характерно для шасі блока, який встановлено за направляючими у приладову стійку або при встановленні плати за направляючими у блок ЕА.

Формули для розрахунку згинаючих моментів і напружень у цьому випадку будуть аналогічні (8. 3) і (8. 4), де коефіцієнти 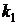, 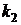визначатимуться за даними табл. 8. 2. Стріла прогину розраховується як

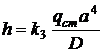, (8. 6)

де 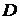– циліндрична жорсткість пластини, яка знаходиться за формулою (7. 4);

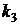– коефіцієнт, значення якого наведено у табл. 8. 2.

Таблиця 8. 2 – Значення коефіцієнтів 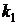, , 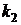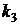для випадку жорсткого

закріплення двох сторін

	Дві більші сторони жорстко закріплені, інші – вільно оперті			Дві короткі сторони жорстко закріплені, інші – вільно обперті

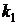
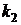
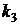
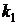
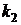
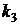
1, 00	0, 020	0, 026	0, 0148	0, 020	0, 026	0, 0148
1, 10	0, 026	0, 024	0, 0175	0, 021	0, 028	0, 017
1, 20	0, 030	0, 031	0, 022	0, 032	0, 033	0, 023
1, 40	0, 038	0, 038	0, 028	0, 039	0, 040	0, 030
1, 60	0, 039	0, 040	0, 029	0, 041	0, 042	0, 032
2, 00	0, 041	0, 042	0, 032	0, 440	0, 044	0, 035

3. Випадок жорсткого закріплення пластини з трьох сторін при вільно обпертій четвертій (рис. 7. 2, варіанти 7 і 8), що характерно для жорсткого з’єднання шасі блока з двома боковими стінками і передньою або задньою панеллю.

У цьому випадку для розрахунку згинаючих моментів, напружень і деформації необхідно скористатися формулами (8. 3), (8. 4) і (8. 6), а значення коефіцієнтів вибрати за даними табл. 8. 3.

Таблиця 8. 3 – Значення коефіцієнтів 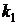, , 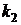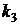при жорсткому закріпленні трьох сторін і вільно обпертій четвертій

	Коротка сторона вільно оперта			Довга сторона вільно оперта

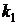
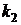
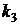
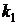
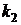
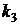
1, 00	0, 0204	0, 0256	0, 002	0, 9204	0, 256	0, 002
1, 11	0, 019	0, 029	0, 002	0, 026	0, 257	0, 002
1, 25	0, 018	0, 033	0, 002	0, 033	0, 027	0, 002
1, 43	0, 015	0, 036	0, 002	0, 040	0, 026	0, 003
1, 66	0, 012	0, 044	0, 002	0, 050	0, 025	0, 003
2, 00	0, 010	0, 041	0, 002	0, 055	0, 018	0, 004

4. Випадок зосередження маси по поверхні пластини.

У попередніх пунктах розглянуто випадки, коли статичне навантаження, обумовлене дією сил тяжіння, можливо вважати рівномірно розподіленим за поверхнею пластини. Однак це припущення не завжди справедливе, наприклад, при зосередженні мас у центрі пластини таке навантаження слід вважати зосередженим. Якщо зосереджене статичне навантаження характеризується силою Р, що діє перпендикулярно пластині в її центрі, то згинаючі моменти відносно осей 0х, 0у розраховуються аналогічно випадку жорсткого закріплення всіх сторін пластини (8. 3) з коефіцієнтами 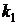, , 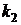вибраними за табл. 8. 4. Напруження та деформація конструкції визначатиметься за формулами:

;

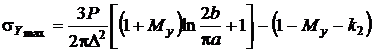; (8. 7)

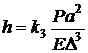де 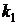, , 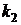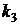– коефіцієнти, значення яких наведено у табл. 8. 4.

Таблиця 8. 4 – Значення коефіцієнтів 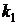, , 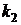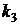для розрахунку напружень і деформації при дії зосередженого навантаження

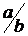
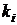
1, 0	1, 2	1, 4	1, 6	1, 8	2, 0	3, 0
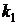
-0, 515	-0, 310	-0, 191	-0, 120	-0, 068	-0, 040	0, 0
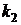
0, 130	0, 110	0, 080	0, 050	0, 030	0, 023	0, 0
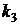
0, 101	0, 137	0, 142	0, 150	0, 156	0, 166	0, 170

Слід мати на увазі, що у п. 1–4 наведено вирази для визначення фактичних значень напружень і деформації. Їх необхідно порівняти з допустимими. У наближених розрахунках допустимі напруження розраховуються за формулами:

- для пластичних матеріалів 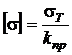; (8. 8)

- для крихких матеріалів ,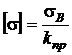

де 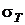, 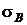– межа текучості та тимчасовий опір відповідно;

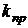– коефіцієнт запасу міцності, що для побутових ЕА приймається рівним:

- для пластичних матеріалів – 1, 4... 1, 8;

- для крихких матеріалів – 2, 0... 5, 0.

У табл. 7. 2 наведено значення величин 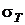, 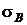для деяких матеріалів.

Завищення значення коефіцієнта запасу міцності під час проектування приводить до збільшення матеріалоємності та собівартості конструкції. Однак, якщо, наприклад, на платі є отвір, то можлива концентрація напруження у краю отвору, яка доходить до значення максимальної напруги, що у два-три рази перевищує відповідне значення для пластини без отвору. У подібних випадках коефіцієнт запасу міцності слід збільшити.

Допустиму величину деформації встановлюють у залежності від ряду факторів: від прийнятої моделі жорсткості пластини, тоді, наприклад, вважають необхідність виконання умови (8. 1); або від допустимої величини мінімального зазору між елементами конструкції, яка може змінюватися за наявності механічних навантажень, тоді припускають, наприклад, 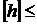2 мм або інше.

8. 2. 2 Розв’язання задачі синтезу

Під час розв’язання задачі синтезу необхідно визначити параметри конструкції, які не задано, наприклад, товщину друкованої плати за умови, щоб величина деформації або виникаючих напружень не перевищували необхідних значень. До такого типу задач відноситься і вибір матеріалу плати при заданих її геометричних розмірах та деякі інші.

Так, наприклад, для визначення необхідної товщини плати при вибраному матеріалі для забезпечення міцності, необхідно розв’язати рівняння (8. 4) відносно 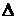, тоді маємо:

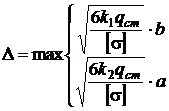. (8. 9)

Для знаходження товщини плати за умови забезпечення необхідної жорсткості слід розв’язати (8. 5) відносно 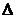, тоді:

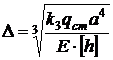. (8. 10)

За необхідності вибору товщини плати за умови забезпечення і міцності і жорсткості слід із значень товщини 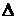, одержаних за формулами (8. 9) і (8. 10), вибрати більше.

8. 2. 3 Порядок виконання роботи

1. Проаналізувати друкований модуль ЕА, який розглядався на практичному занятті №7. Визначити, який характер має статичне навантаження: рівномірно розподіленим чи зосередженим.

2. Розрахувати за вказівками п. 8. 2. 1 діючі напруження в конструкції та деформацію плати, використовуючи, в залежності від варіанта закріплення модуля, необхідні співвідношення.

3. Визначити допустимі напруження та деформацію (прогин) пластини за умов (8. 8) та (8. 1). Порівняти розраховані фактичні значення напружень та деформації у конструкції з допустимими.

4. За результатами порівняння запропонувати конструктивні заходи для збільшення міцності та жорсткості несівної конструкції.

8. 3 Контрольні запитання і завдання

1. Які види механічних впливів ви знаєте? Наведіть їх характеристики.

2. Наведіть конструктивні заходи збільшення міцності та жорсткості різних несівних конструкцій.

3. На які параметри ЕА найбільш суттєво впливають механічні навантаження? Наведіть приклади такого впливу.

4. Які пластини вважаються жорсткими, гнучкими та мембранними?

5. Чим обумовлена величина деформації (прогину) пластини за наявності статичного навантаження?

6. Як впливає жорсткість закріплення сторін пластини на величину напружень, які виникають у конструкції?

7. Які параметри матеріалу пластини впливають на величину напружень, що виникають у конструкції? Її прогин?

8. У чому різниця розрахунків міцності і жорсткості конструкції в залежності від характеру розподілення маси?

9. Наведіть порядок визначення допустимої величини мінімального зазору між елементами несівної конструкції.

10. Наведіть свої міркування щодо вибору матеріалу плати друкованого модуля для забезпечення необхідної міцності, якщо відомо його розміри.

8. 4 Приклади аудиторних і домашніх задач

Завдання. Визначити величину питомого статичного навантаження друкованого модуля, маса встановлених елементів якого 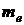= 25 г. Площа поверхні друкованої плати модуля – 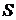= 0, 005 м², її маса – 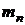= 15 г.

Розв’язання.

Величина питомого статичного навантаження для друкованого модуля:

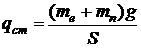де g – прискорення сили тяжіння, м/с².

Підставимо до формули відомі величини. Маємо:

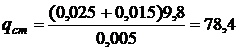(кг/м× с²).

Відповідь: питоме статичне навантаження модуля дорівнює 78, 4 кг/м× с².

9 ОЦІНКА МІЦНОСТІ ТА ЖОРСТКОСТІ НЕСІВНИХ ЕЛЕМЕНТІВ КОНСТРУКЦІЇ ЕА ПРИ ВІБРАЦІЙНИХ НАВАНТАЖЕННЯХ

⇐ Предыдущая 1 2 3 456 7 8 Следующая ⇒